【计算方法】线性方程组的数值解法

题外话：
我上学期做了笔记的科目好像都炸了。。像Java还有数据结构。计算方法也来做一个吧，反正迟早是要炸的

一、综述

线性方程组的解法可以分为两类：直接法和迭代法。
直接法通过有限四次运算得到精确解，比如克莱姆法则和高斯消元法
迭代法通过运用一定的规则进行迭代，逐次逼近，比如Jacobi迭代法，G-S迭代法以及超松弛迭代法（SOR法）
一般来说，直接法精确，迭代法运算快并且容易实现

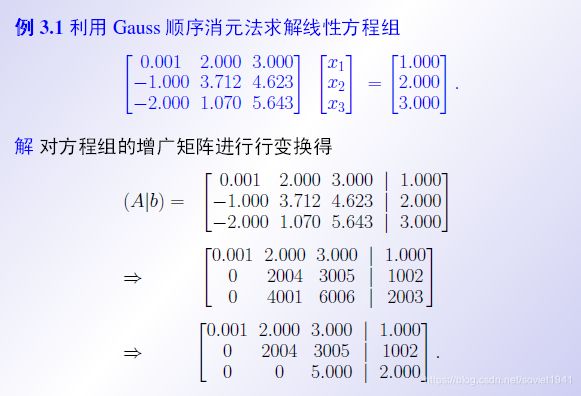
二、高斯消元法

高斯消元法是直接法的一种，在线性代数里讲过
基本思想是先拿第一行作为基准，然后对每一行乘以一个系数，使得这个系数乘以第一行后加上这一行，恰好能把该行第一列的数消掉。
然后第一列的数消掉以后，再对之后几列进行迫害。总之最后会消成一个上三角阵。
这种方法的总体过程是一个消元-回代的过程。

局限性：

1. 所有主元素都不能为0，否则运算将无法进行。
2. 主元素绝对值不能过小，否则将引起较大舍入误差。（这里计算误差用的是2范数）

舍入误差：是指由于计算机表示位数的有限，计算机就会将其舍成一定的位数（例如四舍五入），引起舍入误差。
截断误差：是指计算某个算式时没有精确的计算结果，如积分计算，无穷级数计算等，我们只能截取有限项进行计算，这就是截断误差。

三、高斯选主元消元法

每次消元过程中，要拿来作为系数对照的最上一行最前一列元素，称为主元。

1、完全选主元法

完全选主元法把先把行之间做交换，再把列之间做交换，使得绝对值最大的值在主元位置。

2、选列主元法

完全选主元有点浪费时间，可以只做行的交换，使得头一列的绝对值最大的数跑到主元位置。

四、三角分解法

三角分解法属于直接法之一。
三角分解法的核心思想是将AX=B中的A拆解成A=LU，其中L是单位下三角阵，U是上三角阵。所以三角消元法又称为LU消元法
把A化成LU的思想依据来源高斯消元法，过程很复杂就不推导了

下面运用LU法的步骤
AX=B
=>LUX=B（A=LU）
=>LY=B（UX=Y）
其中LY=B和UX=Y形式在高斯消元法中喜闻乐见。

下面的问题是如何求L和U
LU=A采用待定系数法。求解顺序是U第一行，L第一列，U第二行，L第二列…
如此，便可求解出L和U，之后就是用LY=B求出Y，再用UX=Y求出X。

五、追赶法

追赶法常用于三对角阵，这在某些问题中很常见。是高斯迭代法的又一变种，属于直接法

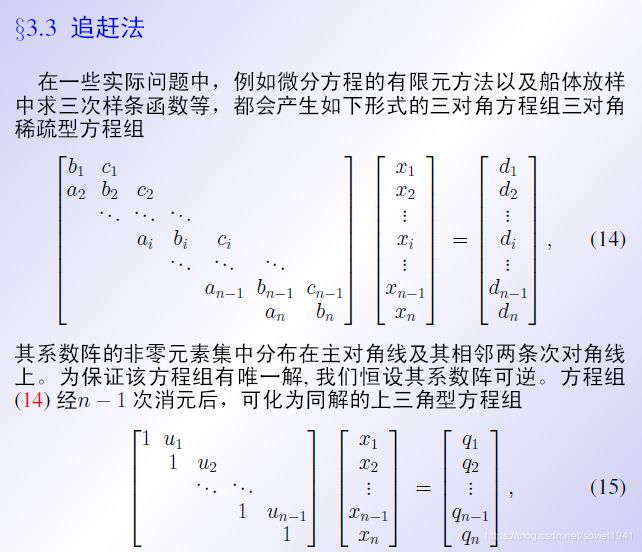
核心思想是把三对角阵化成上三角阵
化成上三角阵的步骤：

1. 让b1化成1，第一行对应改变
2. 借助第一行消去a2，第二行对应改变
3. 让b2化成1，第二行对应改变
4. 借助第二行消去a3，第三行对应改变
5. 让b3化成1，第三行对应改变
   ……
   消元的过程称为追，回代称为赶，因此这个过程也被称为追赶法。

条件数：用于衡量方程组是否对小扰动敏感，即是否病态。
cond(A)₁ = ||A^-1||₁ ||A||₁
cond(A)₂ = ||A^-1||₂ ||A||₂
cond(A)_∞ = ||A^-1||_∞ ||A||_∞

六、Jacobi迭代法

为了方便迭代，将AX=B中的A，分解成 A=L+D+U
其中，L是源自A的严格下三角阵，D是源自A的主元，U是源自A的严格上三角阵

(L+D+U)X = B
=>DX = -(L+U)X + B (首先，要保留含X项，因为要迭代；其次保留DX，因为D是对角矩阵好求逆)
=>X = -D^-1 (L+U)X +D^-1B （同除D）
=>X^(k+1) = -D^-1 (L+U)X^(k) +D^-1B

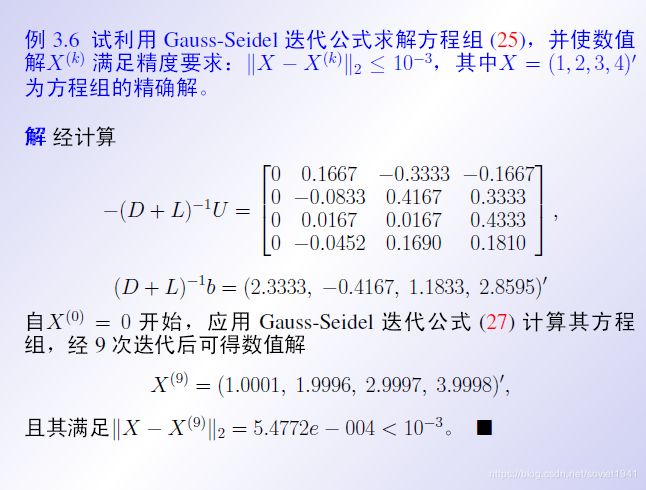
七、G-S迭代法

G-S迭代法全称Gauss-Seidel迭代法
这种方法认为把D也掺和进来精确度更高

(L+D+U)X = B
=>(D+L)X = UX + B (首先，要保留含X项，因为要迭代；其次保留DX，因为D是对角矩阵好求逆)
=>X = -(D+L)^-1 UX +(D+L)^-1B （同除D）
=>X^(k+1) = -(D+L)^-1 UX^(k) +(D+L)^-1B

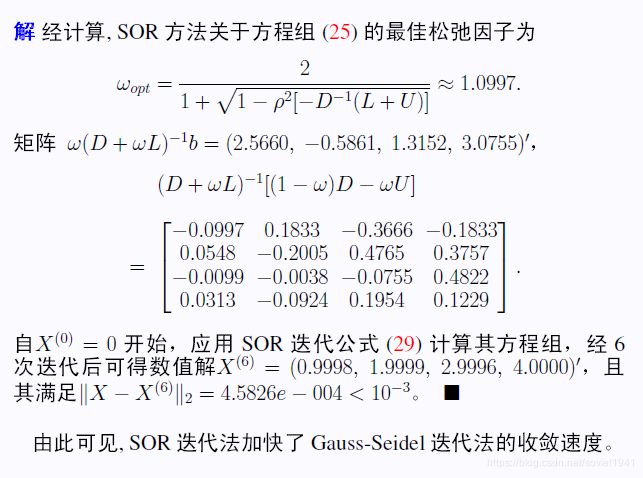
八、SOR法

对于G-S迭代法，等式右边同时加上DX^(k)，有
DX^(k+1) = DX^(k) + ( B - LX^(k+1) - (D + U)X^(k) )
引入松弛因子ω（当作是对后式进行调节），改写为
DX^(k+1) = DX^(k) + ω( B - LX^(k+1) - (D + U)X^(k) )
提取出系数，最后推导出
X^(k+1) = (D+ωL)^-1{ [(1-ω)D-ωU] X^(k) + ωB}
这被称为SOR法，即逐次超松弛迭代法

ω的选取可以最优化，公式见上。

九、迭代法收敛的条件

从计算方法第二章中得到启发，我们认为迭代法总可以写成如下迭代格式
X^(k+1) = BX^(k) + F
如果有
lim X^(k) = X^*
那么迭代格式就是收敛的

迭代格式收敛的充要条件：
谱半径ρ(B) < 1 <===> 迭代格式收敛

在某些情况下，计算谱半径是困难的，可以使用一些充分条件判定迭代收敛
存在一个矩阵范数使||B|| < 1 ==> 迭代格式收敛

同时，也可以根据以下定理
如果AX=B中的A严格对角占优，那么迭代格式收敛
A严格对角占优 ==> 迭代格式收敛

严格对角占优：主元素的绝对值大于该行其他值绝对值之和