求解线性方程的数值方法——Matlab中实现算法

求解线性方程的数值方法

求解线性方程的数值方法主要包括以下几种：

• 二分法
• 牛顿法
• 简化牛顿法
• 弦截法

实现代码见博客最后

---

算法实现

• 用二分法、牛顿法、简化牛顿法、弦截法分别计算115的平方根，精确到小数点后六位

设计思路

• 首先罗列出方程y = x^2-115，而要求的平方根就在于跟x轴的交点，也就是零点处
• 具体迭代的方法见代码
• 迭代结束的标志是前后两次迭代的结果，相差小于小数点后六位，也就是log10（a-b）< -6

数值实验

• 二分法迭代步数跟收敛精度的关系图
  

• 牛顿法迭代步数跟收敛精度的关系图
  

• 简化牛顿法迭代步数跟收敛精度的关系图
  

• 弦截法迭代步数跟收敛精度的关系图
  

• 四种方法的迭代时间对比
  
  

结果分析

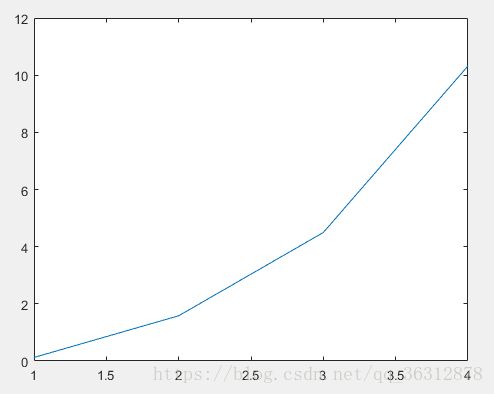
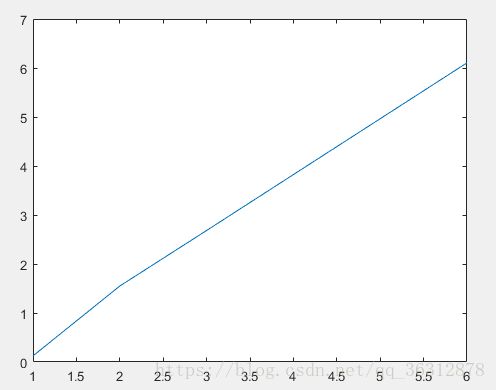
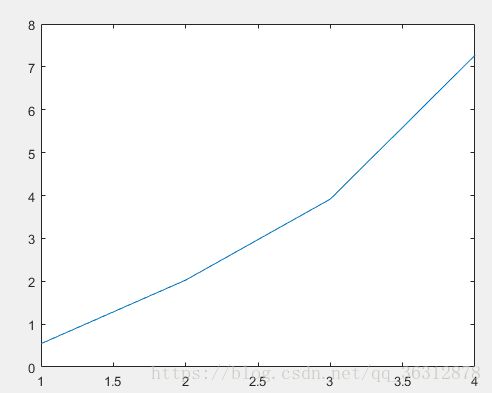
• 从迭代步数上看，相同的求解的结果如下：

求解方法	迭代步数
二分法	20
牛顿法	4
简化牛顿法	6
弦截法	4

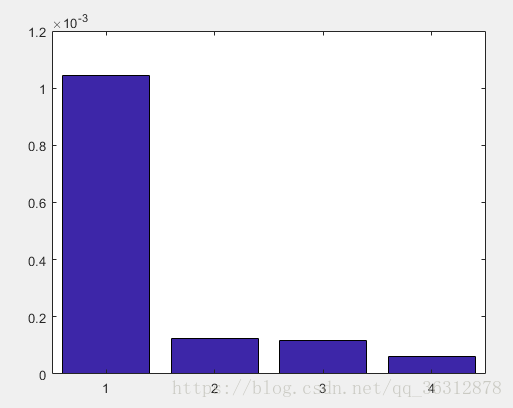
- 从时间上看，二分法的迭代时间明显高于其他三种方法，其他三种方法的迭代时间不分上下。总体而言，在本次求解中，牛顿法可能速度稍微快一点，简化牛顿法由于迭代步数较多，迭代时间会稍微长一点。

实现代码

• 二分法

clear;
format long;
a = 10;
b = 11;
res = binary(a,b);
x = res(1,:);
y = res(2,:);
y = -y;
plot(x,y);

function result = binary(a, b)

    k = 0;
    acc = -6;
    now = 0.0;
    x = 0.0;

    while(now >= acc)
        x = (a+b)/2;
        n = x^2-115;
        m = a^2-115;

        if n == 0
            return;
        elseif n*m < 0
            b = x;
        else
            a = x;    
        end

        k = k+1;
        now = log10(b-a);
        result(1,k) = k;
        result(2,k) = now;
    end
    return;
end

• 牛顿法

clear;
format long;
a = 10;
b = 11;
res = newton(10);
x = res(1,:);
y = res(2,:);
y = -y;
plot(x,y);

function result = newton(a)
    x0 = 0.0;
    x1 = a;
    acc = -6;
    k = 0;
    now = 0.0;

    while(now >= acc)
        x0 = x1;
        w = x0^2-115;
        p = 2*x0;
        x1 = x0 - w/p;

        k = k + 1;
        result(1,k) = k;
        now = log10(abs(x1-x0));
        result(2,k) = now;
    end
end

• 简化牛顿法

clear;
format long;
a = 10;
b = 11;
res = newton(10);
x = res(1,:);
y = res(2,:);
y = -y;
plot(x,y);

function result = newton(a)
    x0 = 0.0;
    x1 = a;
    acc = -6;
    k = 0;
    now = 0.0;
    p = 2*a;

    while(now >= acc)
        x0 = x1;
        w = x0^2-115;
        x1 = x0 - w/p;

        k = k + 1;
        result(1,k) = k;
        now = log10(abs(x1-x0));
        result(2,k) = now;
    end
end

• 弦截法

clear;
format long;
a = 10;
b = 11;
res = secant(a, b);
x = res(1,:);
y = res(2,:);
y = -y;
plot(x, y);

function result = secant(a, b)
    x0 = a;
    x1 = b;
    x2 = 0.0;
    w = 0.0;
    p = 0.0;
    k = 0;
    acc = -6;
    now = 0.0;

    while(now >= acc)
        w = x1^2-115;
        p = ((x1^2-115)-(x0^2-115))/(x1-x0);
        x2 = x1 - w/p;

        x0 = x1;
        x1 = x2;
        k = k+1;
        now = log10(abs(x1-x0));
        result(1,k) = k;
        result(2,k) = now;
    end
end

• 时间对比代码

clear;
format long;
a = 10;
b = 11;
x = [1,2,3,4];
y(1) = binary(a, b);
y(2) = newton(a);
y(3) = better_newton(a);
y(4) = secant(a, b);
bar(x,y);

function time = binary(a, b)

    k = 0;
    acc = -6;
    now = 0.0;
    x = 0.0;
    time = 0.0;

    while(now >= acc)
        tic;
        x = (a+b)/2;
        n = x^2-115;
        m = a^2-115;

        if n == 0
            return;
        elseif n*m < 0
            b = x;
        else
            a = x;    
        end

        k = k+1;
        now = log10(b-a);
        toc;
        time = time+toc;
        result(1,k) = time;
        result(2,k) = now;
    end
    return;
end

function time = newton(a)
    x0 = 0.0;
    x1 = a;
    acc = -6;
    k = 0;
    now = 0.0;
    time = 0.0;

    while(now >= acc)
        x0 = x1;
        tic;
        w = x0^2-115;
        p = 2*x0;
        x1 = x0 - w/p;

        k = k + 1;
        toc;
        time = time + toc;
        result(1,k) = time;
        now = log10(abs(x1-x0));
        result(2,k) = now;
    end
end

function time = better_newton(a)
    x0 = 0.0;
    x1 = a;
    acc = -6;
    k = 0;
    now = 0.0;
    time = 0.0;
    p = 2*a;

    while(now >= acc)
        x0 = x1;
        tic;
        w = x0^2-115;
        x1 = x0 - w/p;

        k = k + 1;
        toc;
        time = time + toc;
        result(1,k) = time;
        now = log10(abs(x1-x0));
        result(2,k) = now;
    end
end

function time = secant(a, b)
    x0 = a;
    x1 = b;
    x2 = 0.0;
    w = 0.0;
    p = 0.0;
    k = 0;
    acc = -6;
    now = 0.0;
    time = 0.0;

    while(now >= acc)
        tic;
        w = x1^2-115;
        p = ((x1^2-115)-(x0^2-115))/(x1-x0);
        x2 = x1 - w/p;

        x0 = x1;
        x1 = x2;
        toc;
        time = time + toc;
        k = k+1;
        now = log10(abs(x1-x0));
        result(1,k) = time;
        result(2,k) = now;
    end
end