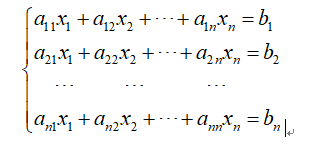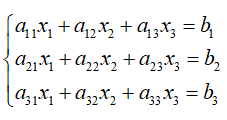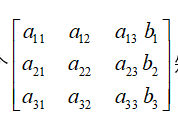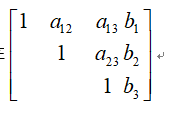数值计算（一）之解线性方程组（高斯消去法，列选主元消去法，全选主元消去法，杜立特尔分解，克洛特分解，乔里斯基分解）

解线性方程组即解一个多元一次方程组，例如

1. 目录

   1. 消去法

      分解法

      ---

 

消去法

原理

没有学过高级的解法也没关系，凭借我们初高中的知识足以解决这个问题

这是一个多元一次方程组，拥有n个未知量，也有n方程

我们可以通过对一个方程组进行同等变形后与其他方程组相加减，消去其他未知量

最后变为一个仅含有一个未知量的方程，求解后逐次回带，接触其他未知数

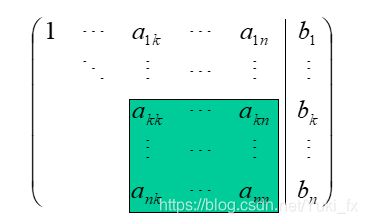
当我们接触了线性代数后，我们可以把这n个方程组的系数提取出来，与等号右边的值共同组成一个增广矩阵，对这个矩阵进行初等行列变换，然后求解。实质上和我们初高中的消元法是一样的。

例如这样一个方程组

我们构造这样一个 矩阵

数值计算这里把解线性方程组的方法系统化，分为消去法，分解法，迭代法。

1分解法

分解法是将我们上面构造的矩阵，进行初等行列变换后，变成单位上三角矩阵或者单位下三角矩阵，然后求解出一个未知数后逐个回带。

高斯消去法就是把矩阵变换为单位上三角矩阵

求解出X3以后逐个回带

 

列选消去法是在上面的基础上进行改进，每次选择对角线下那一列元素绝对值最大的元素，调整到对角线部分，在进行处理，用以减小误差。

全选消去法又是在列选消去法的基础上改进，每次选择从对角线元素开始的右下角矩形部分的最大值，把它放在对角线上，用以减小误差

由于全选消去法可能会交换列，进行列变换，改变变量的位置，所以用计算机求解时需要记录交换的情况，最后把未知数恢复为X1-Xn的顺序

 

高斯消去法

//高斯消去法
void GusElimination(double *p,int row)
{
    double coef;//系数，用于归一化和行处理
    int col=row+1;//保存增广矩阵的列数
    int i,j,k;//循环变量，指示行和列
    for(k=0;k=0;i--)
        for(j=row-1;j>i;j--)
            *(p+i*col+row)-=( *(p+j*col+row) ) * ( *(p+i*col+j) );
    //求解结果保存在增广矩阵的最后一列
}

列选消去法

//列选主元消去法
void ColumnElimination(double *p,int row)
{
    double coef,tmp,Max;
    int Maxrow,col=row+1;
    int i,j,k;

    for(k=0;k Max){
                Max=*(p+i*col+k); Maxrow=i;
            }//End if

        for(j=k;j=0;i--)
        for(j=row-1;j>i;j--)
            *(p+i*col+row)-=( *(p+j*col+row) ) * ( *(p+i*col+j) );
    //求解结果保存在增广矩阵最后一列
}

全选主元消去法

//全选主元消去法
void AllElimination(double *p,int row)
{
    double coef,tmp,Max;//coef表系数，tmp临时变量，Max用来保存绝对值最大元素
    int MaxCol,MaxRow,col=row+1;//MaxCol和MaxRow用来保存绝对值最大元素所在的行和列
    int i,j,k;
    int *a=(int *)malloc(row * sizeof(int));//申请一个临时数组用来保存交换记录
    for(i=0;iMax){
                    Max = fabs(*(p+i*col+j));
                    coef=*(p+i*col+j);
                    MaxRow=i;   MaxCol=j;
                }// End if
            }//End for-j
        }//End for-i

        if(MaxCol != k)//交换k和MaxCol两列，行i的范围从0到Row-1
        {
            for(i=0;i=0;i--)
        for(j=row-1;j>i;j--)
            *(p+i*col+row)-=( *(p+j*col+row) ) * ( *(p+i*col+j) );

    for(i=0;i *(a+j+1) )
            {
                tmp = *(a+j);
                *(a+j)=*(a+j+1);
                *(a+j+1)=tmp;

                tmp = *(p+j*col+row);
                *(p+j*col+row)= *(p+(j+1)*col+row);
                *(p+(j+1)*col+row)=tmp;
            }//End if
        }//End for-j
    }//End for-i
    free(a);
}

分解法

原理

消去法是增广矩阵化为单位上三角矩阵求解，除此之外，还有另外一种解题思路

那就是：将矩阵A分解成两个三角形矩阵L和U的乘积，其中L为下三角矩阵，U为上三角矩阵，则 ：

可以证明，当系数矩阵的各阶顺序主子式不为0时，这样的分为有且仅有一组

 

在这种思路下，就有三种分解方法，

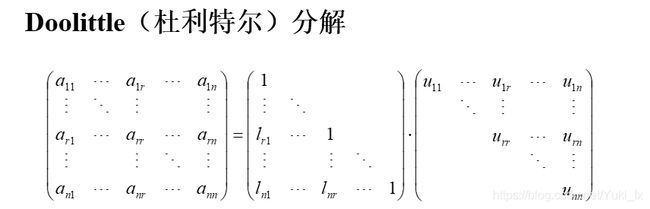
Doolitte分解法：L是单位下三角矩阵，U是上三角矩阵

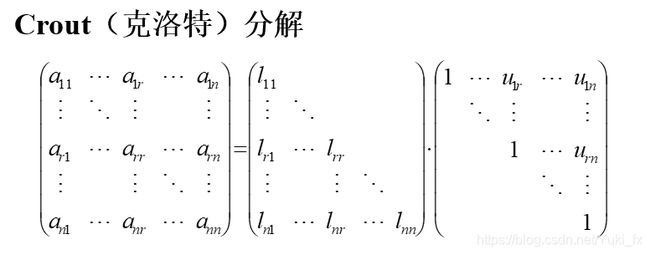
Crout分解法：L是下三角矩阵，U是单位上三角矩阵

 

Cholesky分解法：L和U互为转置矩阵

要进行这样的分解，系数矩阵A就要满足是对称正定矩阵

对称：矩阵中的元素关于对角线对称

正定：矩阵所有的特征值都大于0

 

三角分解法不需要特别记住什么公式，只需要知道矩阵乘法的运算方式

进行一次逆运算，先计算某一个矩阵的行，在计算另外一个矩阵的列，以此往复。

杜立特尔分解法

//杜立特尔分解法,分解为单位下三角和上三角矩阵
void Doolittle(double *p,int row)
{
    int i,j,k,col=row+1;//增广矩阵的列
    double sum;//保存求和结果

    for(k=0;k=0;i--)//通过Ux=y求解x
    {
        for(j=row-1;j>i;j--)
            *(p+i*col+row)-=( *(p+j*col+row) ) * ( *(p+i*col+j) );
        ( *(p+i*col+row) )/=( *(p+i*col+i) );
    }//End for-i
    for(i=0;i

克洛特分解法

//克洛特尔分解法，分解为单位上三角和下三角矩阵
void Crout(double *p,int row)
{
    int i,j,k;
    int col=row+1;
    double sum;

    for(k=0;k=0;i--)//通过Ux=y求解x
        for(j=row-1;j>i;j--)
            *(p+i*col+row)-=( *(p+j*col+row) )*( *(p+i*col+j) );

    for(i=0;i

乔里斯基分解法

//乔里斯基分解，分解为两个互为转置矩阵的矩阵
void Cholesky(double *p,int row)
{
    int i,j,k;
    int col=row+1;
    double sum;

    for(k=0;k=0;i--)
    {//通过Ux=y求解结果x
        for(j=row-1;j>i;j--)
            *(p+i*col+row)-=( *(p+i*col+j) )*( *(p+j*col+row) );
        *(p+i*col+row)/=( *(p+i*col+i) );
    }

    for(i=0;i