编译原理第三章 词法分析
知识总结
一、词法分析器
1、功能:输入源程序,输出单词符号
2、单词符号常常用二元式来表示:<单词种别,单词符号的属性值>
(1)单词种别:通常用整数编码来表示
一字一种:关键字,运算符,界符
按类型:常数
统归一种:标识符
(2)单词符号的属性值:反映单词特性或特征的值
3、词法分析器运作过程(词法分析器设计):
输入源程序文本->输入串放入输入缓冲区->预处理子程序预处理输入串->预处理好的子程序放到扫描缓冲区->
在缓冲区进行单词符号的识别
4、单词符号的识别方法:
(1)超前搜索:向前多读几个符号,一旦确定识别到的单词之后,需要进行扫描指针的回退
(2)直接分析法:根据读来的第一个字符的种类分别转到各种子程序处理
(3)状态转换图:一张有限方向图,能够识别(接受)一定的符号串
结点:代表状态,用圆圈表示
箭弧:状态之间用箭弧连接
箭弧上的标记:代表在射出节点下可能出现的输入字符或字符类
一个状态转换图包含有限个状态,其中有一个初态,至少要有一个终态(用双圆圈表示)
二、正规表达式与有限自动机
1、正规式:有限次使用下述三个步骤而得到的表达式:
(1)ε和φ是∑上的正规式,它们所表示的正规集分别为{ε}和φ
(2)任何a∈∑,是∑上的一个正规式,他所表示的正规集为{a}
(3)假定U和V都是∑上的正规式,他们所表示的正规集分别记为L(U)和L(V),那么:
a.(U|V)是正规式,所表示的正规集为L(U)∪L(V)
b.(UV)是正规式,所表示的正规集为L(U) · L(V)(连接积)
c.(U)*是正规式,所表示的正规集为 (L(U))*(闭包)
2、正规集:仅由这些正规式所表示的字集
3、非确定的有限自动机NFA(Non-deterministic Finite Automata)
定义:一个非确定有限自动机(NFA)M是一个五元式:M = (S, ∑, f, S0, F),其中:
- S是一个有限的状态集合
- ∑是一个有穷的输入符号的字母表
- f是从S×∑*到S的子集的部分映射,即:S×∑*->2s
- S0是初始状态集合
- F是终态集
4、确定的有限自动机DFA(Deterministic Finite Automata)
定义:一个确定有限自动机(DFA)M是一个五元式:M = (S, ∑, f, s0, F),其中:
- S是一个有限的状态集合
- ∑是一个有穷的输入符号的字母表
- f是从 S×∑->S的单值部分映射
- s0是S中的一个元素,是唯一的初态
- F是终态集 (可空)
5、表示方法:
(1)状态转换矩阵(实际是一个表):行表示状态,列表示输入字符,矩阵元素f(s,a)的值
(2)状态转换图
6、DFA是NFA的特例,对于每个NFA M存在一个DFA M’使得L(M) = L(M’),即M和M’等价
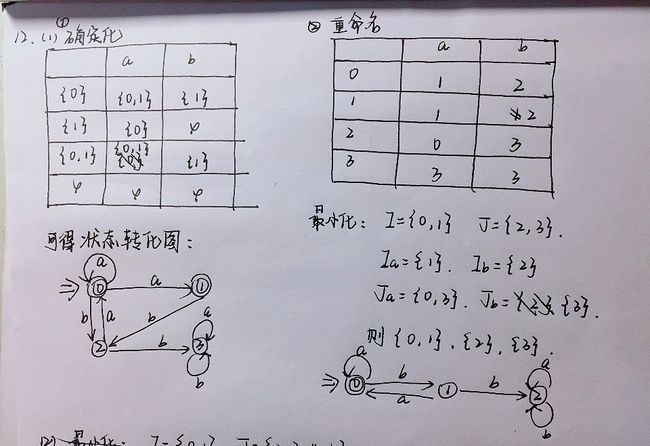
NFA确定化为DFA:子集法
(1)假定I是M’的状态集的子集,定义I的ε闭包ε_CLOSURE(I)为:
a.若q∈I,则q∈ε_CLOSURE(I)
b.若q∈I,那么从q出发经任意条ε弧而能到达的任何状态q’都属于ε_CLOSURE(I)
(2)假定I是M’的状态集的子集,a∈∑,定义Ia =ε_CLOSURE(J),
J是所有可从I中的某一状态结点出发经过一条a弧而到达的状态结点的全体
求Ia:先根据集合I,求集合J(一条a弧);然后求J的ε闭包ε_CLOSURE(J)
三、正规式与有限自动机的等价性
1、对于任何∑上的NFA M都可构造一个∑上的正规式r,使得L(r)=L(M)
多变少,合并,替换规则如下:
2、对于∑上的正规式r,存在一个∑上的DFA M,使得L(M) = L(r)
少变多,分裂,步骤如下:
(1)根据r构造一个NFA M',使得L(M’) = L(V)
(2)将M'确定化,变为DFA M(子集法)
四、确定有限自动机的化简
即寻找一个状态数比M少的DFA M’,使得L(M’) = L(M)
1、化简算法思想:
将M的状态集分割成一些不相交的子集,使得:
- 任何不同的两个子集状态都是可区别的
- 同一个子集中的任何状态都是等价的
最后在每个子集中选一个代表,同时消去其它等价状态
2、化简步骤:
(1)检查状态转换函数是否为全函数。
全函数是指每个状态对每个输入符号都有转换
(2)用化简算法进行化简
(3)去掉死状态
课后习题
总结感悟
本章的重点知识是正规式与有限自动机的相互转化。确定有限自动机DFA是非确定有限自动机NFA的特例,当我们知道一个正规式可以将其转化为有限自动机,反之当知道一个有限自动机也可以写出它的正规式,这两者是一个等价的关系。有限自动机到正规式是一个多变少的过程,要按替换规则进行合并;正规式到有限自动机是一个少变多的过程,要进行分裂,先构造NFA,然后把NFA按子集法确定化为DFA。通过这一章的学习我对编译原理的概念又有了一个更深一步的认识,这些概念的是十分抽象的,看知识点和课本例题时感觉自己掌握了,但是自己做起课后题来还是比较吃力的。