如何利用MATLAB对常微分方程进行数值求解?
文章目录
- 前言
- 1 常微分方程
- 1.1 常微分方程的概念
- 1.2 常微分方程的定义
- 1.3 常微分方程数值求解的一般概念
- 2 常微分方程数值求解函数
- 3 刚性问题
- 结语
前言
今天我们要说的就是利用MATLAB对常微分方程进行数值求解。本文是科学计算与MATLAB语言专题六第5小节的学习笔记,如果大家有时间的话,可以去听听课,没有的话,可以看看我的笔记,还是很不错的。
1 常微分方程
1.1 常微分方程的概念
在初等数学中就有各种各样的方程,比如线性方程、二次方程、高次方程、指数方程、对数方程、三角方程和方程组等等。这些方程都是要把研究的问题中的已知数和未知数之间的关系找出来,列出包含一个未知数或几个未知数的一个或者多个方程式,然后取求方程的解。
但是在实际工作中,常常出现一些特点和以上方程完全不同的问题。比如:物质在一定条件下的运动变化,要寻求它的运动、变化的规律;某个物体在重力作用下自由下落,要寻求下落距离随时间变化的规律;火箭在发动机推动下在空间飞行,要寻求它飞行的轨道,等等,要以现有数据求得出形式上的函数解析式,而不是以已知函数来计算特定的未知数。
物质运动和它的变化规律在数学上是用函数关系来描述的,因此,这类问题就是要去寻求满足某些条件的一个或者几个未知函数。也就是说,凡是这类问题都不是简单地去求一个或者几个固定不变的数值,而是要求一个或者几个未知的函数。
解这类问题的基本思想和初等数学解方程的基本思想很相似,也是要把研究的问题中已知函数和未知函数之间的关系找出来,从列出的包含未知函数的一个或几个方程中去求得未知函数的表达式。但是无论在方程的形式、求解的具体方法、求出解的性质等方面,都和初等数学中的解方程有许多不同的地方。
在数学上,解这类方程,要用到微分和导数的知识。因此,凡是表示未知函数的导数以及自变量之间的关系的方程,就叫做微分方程。1
1.2 常微分方程的定义
定义1:凡含有参数,未知函数和未知函数导数 (或微分) 的方程,称为微分方程,有时简称为方程,未知函数是一元函数的微分方程称作常微分方程,未知函数是多元函数的微分方程称作偏微分方程。微分方程中出现的未知函数最高阶导数的阶数,称为微分方程的阶。定义式如下:
F ( x , y , y ′ , y ′ ′ , … , y ( n ) ) = 0 F(x,y,y',y'',…,y^{(n)})=0 F(x,y,y′,y′′,…,y(n))=0
定义2:任何代入微分方程后使其成为恒等式的函数,都叫做该方程的解。
若微分方程的解中含有任意常数的个数与方程的阶数相同,且任意常数之间不能合并,则称此解为该方程的通解(或一般解).
当通解中的各任意常数都取特定值时所得到的解,称为方程的特解。
一般地说, n n n阶微分方程的解含有 n n n个任意常数。
也就是说,微分方程的解中含有任意常数的个数和方程的阶数相同,这种解叫做微分方程的通解。通解构成一个函数族。
如果根据实际问题要求出其中满足某种指定条件的解来,那么求这种解的问题叫做定解问题,对于一个常微分方程的满足定解条件的解叫做特解。
对于高阶微分方程可以引入新的未知函数,把它化为多个一阶微分方程组。2
1.3 常微分方程数值求解的一般概念
求解常微分方程初值问题就是寻找函数 y ( t ) y(t) y(t)使之满足如下方程:
y ′ = f ( t , y ) , t 0 ≤ t ≤ b , y ( t 0 ) = y 0 y'=f(t,y),t_0≤t≤b, y(t_0)=y_0 y′=f(t,y),t0≤t≤b,y(t0)=y0
所谓其数值解法,就是求 y ( t ) y(t) y(t)在离散结点t处的函数近似值 y y y。的方法, y n ≈ y x n y_n\approx y_{xn} yn≈yxn。
这些近似值称为常微分方程初值问题的数值解。相邻两个结点之间的距离称为步长。
单步法:在计算 y n + 1 y_{n+1} yn+1时只用到前一步的 y n y_n yn,因此在有了初值之后就可以逐步往下计算,其代表是龙格-库塔(Runge-Kutta)法。$$
多步法:在计算 y n + 1 y_{n+1} yn+1时,除了用到前一步的值 y n y_n yn之外,还要用到 y n − p ( p = 1 , 2 , … , k , k > 0 ) y_{n-p}(p=1,2,…,k,k>0) yn−p(p=1,2,…,k,k>0)的值,即前面的k步。其代表就是亚当斯 ( A d a m s ) (Adams) (Adams)法。
2 常微分方程数值求解函数
MATLAB提供了多个求常微分方程初值问题数值解的函数,一般调用格式为:
[t,y]=solver(filename,tspan,y0,option)
其中,t和y分别给出时间向量和相应的数值解。
solver为求常微分方程数值解的函数。
filename是定义f(t,y)的函数名,该函数必须返回一个列向量。
tspan形式为[to,tf],表示求解区间。
y0是初始状态向量。
option是可选参数,用于设置求解属性,常用的属性包括相对误差值Re1To1(默认值是 1 0 − 3 10^{-3} 10−3)和绝对误差值AbsTol(默认值是 1 0 − 6 10^{-6} 10−6)。
常微分方程数值求解函数的统一命名格式:odennxx
ode是0rdinary Differential Equation的缩写,是常微分方程的意思。
nn是数字,代表所用方法的阶数。例如,ode23采用2阶龙格-库塔 ( R u n g e − K u t t a ) (Runge-Kutta) (Runge−Kutta)算法,用3阶公式做误差估计来调节步长,具有低等精度。
ode45采用4阶龙格-库塔算法,用5阶公式做误差估计来调节步长,具有中等精度。
xx是字母,用于标注方法的专门特征。
ode15s、ode23s中的“s”代表(Stiff),表示函数适用于刚性方程。
求常微分方程数值解的函数
| 求解函数 | 采用方法 | 适用场合 |
|---|---|---|
| ode23 | 2阶或3阶Runge-Kutta算法,低精度 | 非刚性 |
| ode45 | 4阶或5阶Runge-Kutta算法,中精度 | 非刚性 |
| ode113 | Adams算法,精度可到10-3~10-6 | 非刚性,计算时间比ode45短 |
| ode15s | Gear’s反向数值微分算法,中精度 | 刚性 |
| ode23s | 2阶Rosebrock算法,低精度 | 刚性,当精度较低时,计算时间比ode15s短 |
| ode23tb | 梯形算法,低精度 | 刚性,当精度较低时,计算时间比ode15s短 |
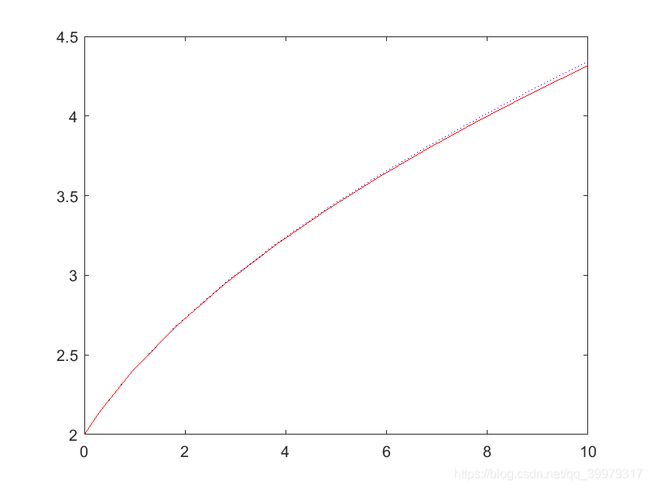
例1求解微分方程初值问题,并与精确解 y ( t ) = t + 1 + 1 y(t)=\sqrt {t+1}+1 y(t)=t+1+1进行比较。
{ y ′ = y 2 − t − 2 4 ( t + 1 ) , 0 ≤ t ≤ 10 y ( 0 ) = 2 \left\{ \begin{aligned} y'&=\frac{y^2-t-2}{4(t+1)},0≤t≤10\\ y(0)&=2 \end{aligned} \right. ⎩⎪⎨⎪⎧y′y(0)=4(t+1)y2−t−2,0≤t≤10=2
f=@(t,y)(y^2-t-2)/4/(t+1);
[t,y]=ode23(f,[0,10],2);
y1=sqrt(t+1)+1;
plot(t,y,'b:',t,y1,'r');
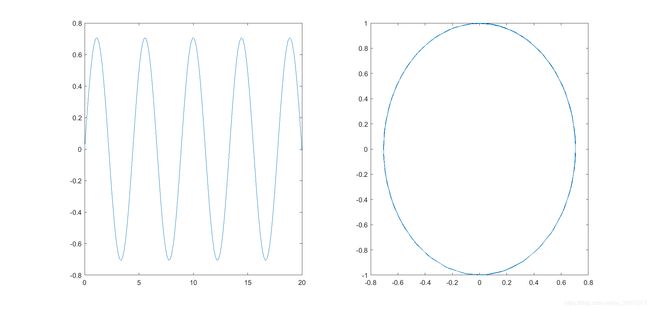
例2已知一个二阶线性系统的微分方程为:
{ d 2 x d t 2 + a x = 0 , a > 0 x ( 0 ) = 0 , x ′ ( 0 ) = 1 \left\{ \begin{aligned} \frac{d^2x}{dt^2} +ax&=0,a>0\\ x(0)&=0 ,x'(0)=1 \end{aligned} \right. ⎩⎨⎧dt2d2x+axx(0)=0,a>0=0,x′(0)=1
取a=2,绘制系统的时间响应曲线和相平面图。令x2=x,x1=x’,则得到系统的状态方程:
{ x 2 ′ = x 1 x 1 ′ = − a x 2 x 2 ( 0 ) = 0 , x 1 ( 0 ) = 1 \left\{ \begin{aligned} x_2'&=x_1\\ x_1'&=-ax_2\\ x_2(0)&=0,x_1(0)=1\\ \end{aligned} \right. ⎩⎪⎨⎪⎧x2′x1′x2(0)=x1=−ax2=0,x1(0)=1
3 刚性问题
有一类常微分方程,其解的分量有的变化很快,有的变化很慢,且相差悬殊,这就是所谓的刚性问题(Stiff)。
对于刚性问题,数值解算法必须取很小步长才能获得满意的结果,导致计算量会大大增加。解决刚性问题需要有专门方法。非刚性算法可以求解刚性问题,只不过需要很长的计算时间。
f=@(t,x)[-2,0;0,1]*[x(2);x(1)];
[t,x]=ode45(f,[0,20],[1,0]);
subplot(1,2,1);
plot(t,x(:,2));
subplot(1,2,2);
plot(x(:,2),x(:,1));
例3假如点燃一个火柴,火焰球迅速增大直至某个临界体积,然后,维持这一体积不变,原因是火焰球内部燃烧耗费的氧气和从球表面所获氧气达到平衡。其简化模型如下:
{ y ′ = y 2 − y 3 y ( 0 ) = λ , 0 ≤ t ≤ 2 / λ \left\{ \begin{aligned} y'&=y2-y3\\ y(0)&=\lambda ,0≤t≤2/\lambda \end{aligned} \right. {y′y(0)=y2−y3=λ,0≤t≤2/λ
其中, y ( t ) y(t) y(t)代表火焰球半径,初始半径是 λ \lambda λ,它很小。分析入的大小对方程求解过程的影响。
lamda=0.01;
f=@(t,y) y^2-y^3;
tic;[t,y]=ode45(f,[0,2/lamda],lamda);toc
disp(['ode45计算的点数' num2str(length(t))]);
时间已过0.005774秒。
ode45计算的点数157
tic和toc函数用来记录微分方程求解命令执行的时间,使用tic函数启动计时器,使用toc函数显示从计时器启动到当前所经历的时间。最后还输出计算的点数,运行结果表明这时常微分方程不算很刚性。
注意:
1 这里的代码易出现错误。例如1和l。
2 λ \lambda λ的拼写应为lambda。
lamda=1e-5;
f=@(t,y)y^2-y^3;
tic;[t,y]=ode45(f,[0,2/lamda],lamda);toc
disp(['ode45计算的点数' num2str(length(t))]);
时间已过 1.729913 秒。
ode45计算的点数120565
这时计算时间明显加长,计算的点数剧增,表明这时常微分方程表现为刚性。
lamda=1e-5;
f=@(t,y)y^2-y^3;
tic;[t,y]=ode15s(f,[0,2/lamda],lamda);toc
disp(['ode15s计算的点数' num2str(length(t))]);
时间已过 0.321166 秒。
ode15s计算的点数98
对于刚性问题,我们需要改变求解算法。我们选择以“s”结尾的函数,他们专门用于求解刚性方程。计算时间大大缩短,计算的点数大大减少。
结语
欢迎大家点赞,收藏⭐,转发,
如有问题、建议,请您在评论区留言哦。
百度百科-常微分方程。 ↩︎
百度百科-常微分方程。 ↩︎