牛顿法及其收敛性

---

0. 引论

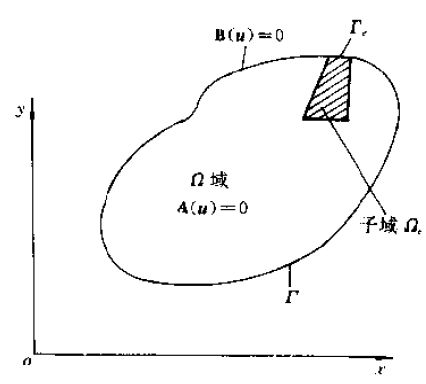
在工程中，很多的问题都可以归结为求解一组偏微分方程。描述如下：在某一个区域\(\Omega\)中，物理量\(u={u_1,u_2,\cdots,u_n}\)满足一组控制方程，并且在边界上满足若干条件：

控制方程利用两个微分算子来表示\(A(u),B(u)\)。
\[ A(u)=\begin{cases} A_1(u)& =0 \\ A_2(u)& =0 \\ &\vdots \end{cases} \in \Omega \]

\[ B(u)=\begin{cases} B_1(u)& =0 \\ B_2(u)& =0 \\ &\vdots \end{cases} \in \partial \Omega \]

以上的问题，只有在求解域比较简单，控制方程形式比较特殊的时候才能求出解析表达，一般情况下，工程问题中的求解域是比较复杂的，控制方程往往是高阶非线性的，这个时候，只能借助于数值求解。偏微分方程的数值解法，常见的有有限元法，有限差分法，有限体积法等。这些数值解法的基本思想是用有限的自由度插值逼近真实解。不管哪一种数值方式，偏微分方程系统离散之后，形成的是常微分方程组或者代数方程组。

在工程中，对于时间维度往往是特别对待的，含有时间项的问题称为非定常问题，也叫瞬态问题，这类问题在空间离散之后，形成的是关于时间的常微分方程，然后利用一些推进求解的方法，将时间维度离散，转换成纯粹的代数方程。而控制方程不含时间项的问题称为稳态问题，对于稳态问题，将控制方程在空间离散之后，形成代数方程组。

可见，不论是那种问题，最后求解的是代数方程组。因此，如何准确高效的求解代数方程组就显得至关重要。这一部分的内容在数值分析里面有详细的介绍，对于工程师来说，一般不必去了解里面艰深的理论，但是，每一种求解方法的适用范围，求解速度，收敛性等重要特征，最好还是要了解。这样才能在使用的时候不至迷茫。

代数方程组可以简记为如下的形式：
\[ F(u)=b \]
还可以表示成为矢量的形式：
\[ Au=b \]
当系数矩阵A与变量u的取值没有关系时，问题时线性的，否在，时非线性问题。众所周知，非线性问题的求解时困难的！！

常用的线性方程组求解方法有：

• 直接法
• • 高斯消去法、矩阵三角分解法（直接分解法、平方根方法、追赶法）、
• 迭代法
• • 雅可比迭代、高斯-赛德尔迭代、超松弛法、块迭代法、共轭梯度法、最速下降法

常用的非线性方程组的求解方法有：

• 迭代法
• • 二分法、不动点迭代、牛顿法、简化牛顿法、牛顿下山法、弦截法、抛物线法
• 多变量不动点迭代法、牛顿法

这里主要介绍牛顿法的一些特性。

---

2. 牛顿法

2.1 单变量牛顿法

对于单变量的牛顿法，大家已经很熟悉了，这里做一点简要的回顾。

方程
\[ f(x)=b \]
给定初值\(x^0\)，利用迭代关系式:
\[ x^{k+1}=x^k-\frac{f(x)-b}{f'(x)} \]
经过一定次数的迭代，就可以收敛到其精确值\(x^*\)。

牛顿法存在两个问题：

1. 当函数的二阶导数在精确解的邻域内小于0时，无法收敛到精确解。
2. 当初值与精确解相差较大时，收敛困难。

2.2 多变量牛顿法

对与多变量牛顿法，其形式可以利用泰勒公式来推导。有\(F(u)=0\)，假设其精确解为\(u^*\)，则有：
\[ F(u^*)=0 \]
将F(u)在精确解处展开，如下：
\[ F(u^*)=F(u)+\nabla F(u)(u^*-u) \]

\[ [\nabla F(u)]^{-1}F(u)=u-u^* \]

因为精确解是不知道的，所以，利用一个初值代替：
\[ u^{k+1}=u^k-[\nabla F(u^k)]^{-1}F(u^k) \]
对于方程(10)所示的迭代式，影响其收敛性的一个重要指标是其Hesse矩阵。Hesse矩阵定义如下：
\[ G(u)=\nabla_u^2F(u) \]
对于多变量牛顿法，\(G(u)\)满足Lipschitz条件：
\[ ||G(y)-G(z)|| <= \beta||y-z|| \]
且\(G(u^*)\)正定，当\(u^0\)充分接近\(u^*\)时，迭代是收敛的，且是二阶收敛。

牛顿法的优点：收敛速度快

缺点：计算量大，收敛条件严格。

---

3. 简化牛顿法

牛顿法具有收敛速度快的特点，但是其缺点也很明显：一是牛顿法计算量很大，每次都要计算Hesse矩阵和\(F(x)\)，并且Hessen矩阵有时计算较为困难。二是要求迭代初值在精确解附近，不然很难收敛。针对上面的问题，有一些改进的牛顿法。这里最为常用的是简化牛顿法（又称平行弦法）和牛顿下山法。

3.1 平行弦法

迭代式为：
\[ \begin{equation} \begin{cases} x^{k+1} & =\phi(x^k) \\ \phi(x^k)& =x^k-Cf(x^k) \end{cases} \end{equation} \]
其中，\(C=\frac{1}{f'(x_0)}\) 。该方法要求迭代式的一阶导数范数小于1才是局部收敛，且是线性收敛。

3.2 牛顿下山法

在迭代过程中，满足单调递减的要求的迭代方法称作下山法。即要求迭代过程中，始终有：
\[ ||f(x^{k+1})||<||f(x^k)|| \]
迭代式：
\[ \begin{equation} \begin{cases} x^{k+1} & =\phi(x^k) \\ \phi(x^k)& =x^k-\lambda\frac{f(x^k)}{f'(x^k)} \end{cases} \end{equation} \]
其中，\(\lambda(0<\lambda \le 1)\)称为下山因子。选择下山因子的时候，从\(\lambda=1\)开始，逐次减半进行试算，直到下降条件（14）成立为止。

转载于:https://www.cnblogs.com/baowee/p/9575408.html