有关群论_置换群_等的简单介绍

群

 

群是一个集合G，连同一个运算"·"，它结合任何两个元素a和b而形成另一个元素，记为a·b。符号"·"是对具体给出的运算，比如整数加法的一般占位符。要具备成为群的资格，这个集合和运算(G,·)必须满足叫做群公理的四个要求：

1.	封闭性：	对于所有G中a, b，运算a·b的结果也在G中。
2.	结合性：	对于所有G中的a, b和c，等式 (a·b)·c = a· (b·c)成立。
3.	单位元：	存在G中的一个元素e，使得对于所有G中的元素a，等式e·a = a·e = a成立。
4.	逆元：	对于每个G中的a，存在G中的一个元素b使得a·b = b·a = e，这里的e是单位元。

进行群运算的次序是重要的。换句话说，把元素a与元素b结合，所得到的结果不一定与把元素b与元素a结合相同；亦即，下列等式不一定恒成立：

（没错就是wiki）

补充：群（G,·）常简记为群G,a·b常简记为ab，a的逆元常简记为；

简单的说：就是定义了由一个集合G与其上的一个运算·组成的东西（G,·），然后她有如上4个性质；

例如：实数集R（除去0）和R上的乘便组成了群——封闭性，结合性显然，单位元为1，x的逆元为1/x;

 

这里还要挂上几个衍生的概念和定理：

 

群的阶：

群中集合的元素个数；

由于我们经常研究集合元素个数有限的群，故用“有限群”和“无限群”两个名词区分之，且这也使群的阶变得有点用了；

 

子群：

对群（G,·），若H是G的子集，且（H,·）是群，则（H,·）是（G,·）的子群；

 

生成集和生成子群：

群G的子集M、所有包含M的G的子群的交构成的子群H，二者是生成集和生成子群的关系，子群H是生成集M的生成子群，记作；

这个定义的含义是：子群H是包含M而又满足群性质的最小集合；

G的任意有交子群的交构成子群H：

　　只要证明H存在封闭性，单位元，逆元即可（结合律是运算的性质而非集合的性质）

• • 　　单位元：单位元e一定属于子群的交，她是子群的共有部分，可见e∈H；
  • 　　逆元：所有包含x的子群都包含x的逆元，可见若x∈H，则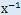∈H；
  •  　　封闭性：若a,b∈H，则ab∈H ？ 若a,b∈H，则a,b属于所有选定的子群，那么ab属于所有选定的子群，即ab∈H；

　　直观的讲，如果x属于子群的交，那么x属于所有子群，那么那些使x满足群性质的东西也必然是所有子群共有的，于是x在子群的交里面也满足群的性质；

 

陪集：

鉴于群不一定有交换律，所以分为左陪集和右陪集；

若H是G的一个子群，a∈G；

则aH={ah|h∈H}是H的左陪集，Ha={ha|h∈H}是H的右陪集；

 

在一个陪集上加载原群的运算不见得是群，

以左陪集为例：

求证：

 可以看出(a*h1)*(a*h2)=a*(h1*a*h2);

于是若a*(h1*a*h2)∈aH，则h1*a*h2∈H；

由于h1,h2∈H，故她们的逆元属于H，则对属于H的上式，乘h1,h2的逆元，也属于H；

即a∈H，与题设矛盾；

这个结论说明陪集上加载原群的运算应该只在a属于H时才是群；

 

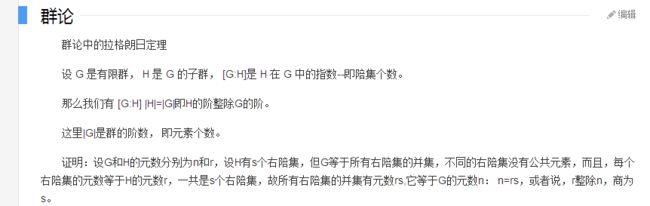
正经的定理1.设H是群G的子群，对任意H的两个左陪集aH和bH，要么aH=bH,要么aH∩bH=∅，对右陪集亦然；

只讨论左陪集；

若存在x∈aH∩bH，则设x=ah1=bh2;

那么，对于任意ah(h∈H)有

由于，故对于任意y∈aH,y属于bH,反之亦然；

于是aH=bH;

对于右陪集亦然；

这个定理是说，随便找一个G的子群H，H的不相等的（左|右）陪集们不重不漏地包含了G的所有元素；

 

一个符号：

记|G:H|表示G中H的不同右的个数，如，设1为G的子群，且只包含单位元，则|G:1|=|G|，即集合G的大小，也即群G的阶；

 

|G:H|=|G|/|H|(这里/是整除)

由于不存在ah1=ah2且h1≠h2（某个不给证明的消去律）所以，所有的H的陪集的大小都等于H的大小,

又由于定理1；

所以|G|=|H||G:H|,即|G:H|=|G|/|H|;

 

正经的定理2.(拉格朗日定理):若H是G的子群，则|G:1|=|G:H||H:1|;

好吧完全是上个引理的翻版么； 

还是要给一个证明：

（感谢度娘。。。证得什么玩意）

 

尽管我们之前的例子中的集合都是仿佛是数集，但是其实对群的大部分研究中，研究的都是集合为（元素是“抽象的事物”的集合）的群；

 如下面要讲的——

 

置换群

 

先讲置换；

 

 置换：

一个有限集X的置换π是从该有限集映至自身的双射；

如果我们把G的元素从1到|X|编号，那么置换π可以看做一个1到|X|的一个排列；

“”（百度知道的一个说法）

其中第i个位置上的数设为，表示编号为i的元素变为编号为ai的元素；

记为：

或直接记为这里相当于，由于上种表达方法的第一排往往是1到|X|，便默认是1到|X|，然后把它省掉；

 

置换群：

置换的群；

有限集X的所有置换的个数为|X|!;

设他们构成集合，在这个集合上搭载运算·，表示对原序列依次进行这两个置换；

于是是个|x|!阶群，

因为该群包含了X的所有置换，而显然是其中一个，封闭；因为没有不可挽回的置换，故逆元存在；还有单位元，结合律存在......；

但是该计算不满足交换律

那么的子群显然也是群，记作；（笔者真变态）

 

几个概念与定理：

 

轨道与等价类：

原数列集合中的元素β，在置换群G中的所有置换中的像，构成的集合叫做β的轨道，记作,我们也称其为包括β的等价类；

 

稳定子群（集）与稳定化子：

有限集X中某m个元素构成了X的一个子集A，置换群G中可以使A中所有元素不动的置换构成的子群叫做A的一个稳定子群，又称稳定集，记为；

该定义在m=1时，需要特别关注，也就是有限集X中的元素k，置换群G中可以使元素k不动的置换构成的子群（对其他元素不做要求），记为G_k，我们也称其为k的稳定化子；

 

轨道-稳定集定理：

|k^G|*|G_k|=|G|;

证明：

有限集X中的某元素k,其轨道为k^G,稳定化子为G_k，设x∈k^G ,集合S_x={$\pi$|$\pi$∈ G ，$\pi$(k)=x},

1. 证明，若x≠y,设$\pi$₁∈S_x，$\pi$₂∈S_y,$\pi$₁G_k与$\pi$₂G_k无交
2. 证明,对于任意$\pi$₁，$\pi$₂∈S_x,陪集$\pi$₁G_k=$\pi$₂G_k;
3. 于是|k^G|=|G:G_k|,套用拉格朗日定理得证；

 

定理1.不相连轮换相乘时可以交换

（显然）

 

定理2.每个（非轮换）的置换都可表为不相连轮换之积；每个轮换都可表为对换之积，因此，每个置换都可表为对换之积

（参见《工程数学--线性代数同济》一书，第一章 行列式 §2 全排列及其逆序数）

 

定理3.每个置换表成对换的乘积时，其对换个数的奇偶性不变

（参见《工程数学--线性代数同济》一书，第一章 行列式 §2 全排列及其逆序数）

（书大概长这样）

 

Burnside引理:

设G是目标集[1,n]上的置换群 
c(f_i)是在置换f_i的作用下不动点的个数（即，f_i属于几个稳定化子？），也就是长度为1的循环的个数。通过上述置换的变换操作后可以相等的元素属于同一个等价类。若G将[1,n]划分成L个等价类，则:

$$L={1\over |G|}\sum_{i=1}^{|G|}c(f_i)$$

证明：

设目标集中的元素i，其轨道为i^G,稳定化子为G_i，

整理上式：

$$L={1\over |G|}\sum_{i=1}^n|G_i|$$

$$L=\sum_{i=1}^n{|G_i|\over |G|}$$

由轨道-稳定集定理变形，得

$$L=\sum_{i=1}^n{1\over i^G}$$

再通过轨道和等价类的定义，即可发现上式成立，于是本引理成立；

证毕；

 

需要指出的是，Burnside引理的表述方法显得更具有一般性，

在她的表述中存在1目标集2置换群3等价类，

注意等价类个数是对于目标集而言的；

如在问题“给出一个正方形，一个旋转群，两种颜色，用两种颜色染正方形的四个角，问有几种在旋转群作用下不同的染法”中

当我们使用Burnside引理思考时，

由于等价类个数这个概念是有几种本质不同的方形，

于是等价类是对于每一个整个正方形而言的，

所以目标集是给所有在不旋转时不同的染色情况编号，

然后还要把旋转群转换为目标集上的置换群（若情况1在旋转a的作用下变为情况2，则置换a使1变为2...）

然后套用该引理即可；

 

Polya定理：

设G是目标集[1,n]上的置换群，设X是以目标集的排列为元素的集合。
m(f_i)是在置换f_i的作用下循环节的个数，通过上述置换的变换操作后X中可以相等的元素属于同一个等价类。若G将[1,n]用k种颜色分别进行染色,然后把X划分成L个等价类，则染色后的等价类个数L为：

$$L=\sum_{i=1}^{|G|}k^{m(f_i)}$$

 (未完待续)

转载于:https://www.cnblogs.com/nietzsche-oier/p/6883880.html