DQN算法分析

Deep Q learning算法分析

Step 1: 用一个深度神经网络来作为Q值的网络，参数为 ω

Q(s,a,ω)≈Qπ(s,a)

Step 2: 在Q值中使用均方差mean-square error 来定义目标函数objective function也就是loss function

L(ω)=E[(r+γ⋅maxa,Q(s,,a,,ω)Target−Q(s,a,ω)2)]

上面公式是 s, ， a, 即下一个状态和动作，这里用了David Silver的表示方式，看起来比较清晰。可以看到，这里就是使用了Q-Learning要更新的Q值作为目标值。有了目标值，又有当前值，那么偏差就能通过均方差来进行计算。

Step 3：计算参数 ω 关于loss function的梯度

∂L(ω)∂ω=E[(r+γ⋅maxa,Q(s,,a,,ω)Target−Q(s,a,ω))∂Q(s,a,ω)∂ω]

Step 4: 使用SGD实现End-to-end的优化目标
有了上面的梯度，而 ∂Q(s,a,ω)∂ω 可以从深度神经网络中进行计算，因此，就可以使用SGD 随机梯度下降来更新参数，从而得到最优的Q值。

DQN训练

• 我们这里分析第一个版本的DQN，也就是NIPS 2013提出的DQN。
  
  
  
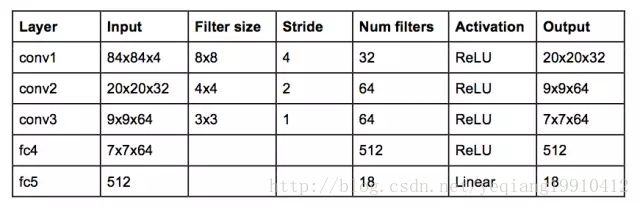
  图1:DQN网络结构图

这个网络的输入是 4 个 84×84 的灰度游戏屏幕。这个网络的输出是是每一个可能动作的 Q 值（Atari 中有 18 个动作）。

图2：NIPS 2013 DQN算法

1、初始化replay memory D 容量为N

2、用一个深度神经网络作为Q值网络，初始化权重参数

3、设定游戏片段总数M

4、初始化网络输入，大小为84*84*4，并且计算网络输出

5、以概率 ϵ 随机选择动作 at 或者通过网络输出的Q（max）值选择动作 at

6、得到执行 at 后的奖励 rt 和下一个网络的输入

7、根据当前的值计算下一时刻网络的输出

8、将四个参数作为此刻的状态一起存入到D中（D中存放着N个时刻的状态）

9、随机从D中取出minibatch个状态

10、计算每一个状态的目标值（通过执行 at 后的reward来更新Q值作为目标值）

11、通过SGD更新weight

• 我们这里分析第二个版本的DQN，也就是NIPS 2015提出的DQN。
  

  
  
  
  图2：NIPS 2015 DQN算法

  1、初始化replay memory D，容量是N 用于存储训练的样本

2、初始化action-value function的Q卷积神经网络 ，随机初始化权重参数θ

3、初始化 target action-value function的 Q^ 卷积神经网络，结构以及初始化权重θ和Q相同

4、设定游戏片段总数M

5、初始化网络输入，大小为84*84*4，并且计算网络输出

6、根据概率 ϵ （很小）选择一个随机的动作或者根据当前的状态输入到当前的网络中 （用了一次CNN）计算出每个动作的Q值，选择Q值最大的一个动作（最优动作）

7、得到执行 at 后的奖励 rt 和下一个网络的输入

8、将四个参数作为此刻的状态一起存入到D中（D中存放着N个时刻的状态）

9、随机从D中取出minibatch个状态

10、计算每一个状态的目标值（通过执行 at 后的reward来更新Q值作为目标值）

11、通过SGD更新weight

12、每C次迭代后更新target action-value function网络的参数为当前action-value function的参数

参考文献：

1. 一个 Q-learning 算法的简明教程
2. 如何用简单例子讲解 Q - learning 的具体过程
3. 《Code for a painless q-learning tutorial》以及百度网盘地址
4. DQN 从入门到放弃4 动态规划与Q-Learning
5. DQN从入门到放弃5 深度解读DQN算法
6. Deep Reinforcement Learning 基础知识（DQN方面）
7. Paper Reading 1 - Playing Atari with Deep Reinforcement Learning
8. Playing Atari with Deep Reinforcement Learning 论文及翻译百度网盘地址
9. Paper Reading 2:Human-level control through deep reinforcement learning
10. Human-level control through deep reinforcement learning 论文及翻译百度网盘地址
11. 重磅 | 详解深度强化学习，搭建DQN详细指南（附论文）
12. Playing Atari with Deep Reinforcement Learning算法解读