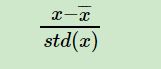小白零基础学习:详解梯度下降算法:完整原理+公式推导+视频讲解
首先简单自我介绍一下,本人现在是国内某211大学2019级博士研究生,计算机科学与技术专业,研究方向和兴趣包括深度学习(CV)、图像处理、菌群仿生优化算法、元胞自动机等,愿与大家分享自己的学习心得!目前主要研究图像去雾算法和深度学习理论。
如果要学习Machine Learning和Deep Learing,那么Gradient Descent Algorithm (梯度下降算法)是必须要掌握的!本篇博文是从零开始详细介绍了梯度下降算法的原理以及公式推导过程,并亲自录制了视频讲解(见文末),力求用最简单、最通俗的语言让小白能完完整整的听得懂。如果大家能看懂文字,就可以不用看视频,如果不想看文字或者文字看起来吃力,那我建议看文字的同时再看视频讲解。
1、从一个“房价预测”的案例开始讲解为什么要用梯度下降算法
我有一个习惯,就是研究一个问题之前一定要问清楚为什么会引入这个概念,为什么要用这个东西?
下面先看这样一张图:
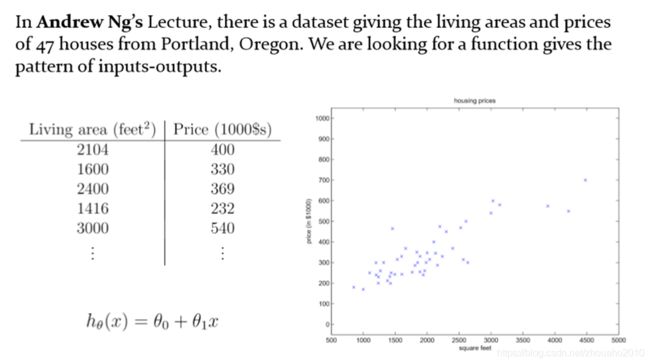 这是我从深度学习大牛吴恩达的课程里面截取的一张图,假设已经收集到波特兰的47个房子的面积以及对应房价,下面让你去预测(或者估计)某一个未知面积的房子房价是多少该怎么办呢?
这是我从深度学习大牛吴恩达的课程里面截取的一张图,假设已经收集到波特兰的47个房子的面积以及对应房价,下面让你去预测(或者估计)某一个未知面积的房子房价是多少该怎么办呢?
这显然就是一个机器学习里面的Supervised Learning(有监督学习)的问题,那我们建设建立了一个Linear Regression回归模型,即建立一个房价和房子面积的函数关系,如:
![]()
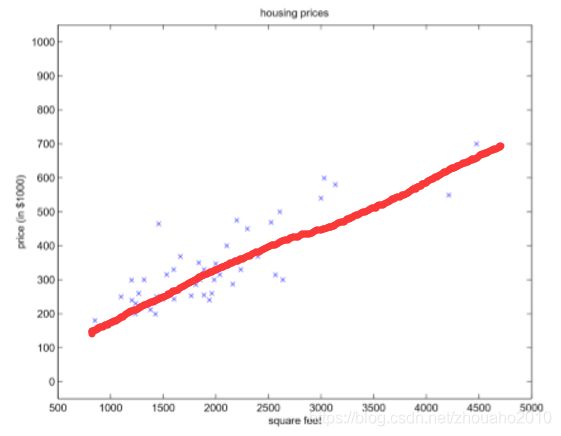
这里面的 h θ h_{\theta } hθ(x)称为假设函数,在机器学习力就是Target目标或者叫Label标签,在这个问题里就是房价,x就是房屋面积,那我们要做的就是通过已有的47个Examples(一般称为训练样本)数据去计算出(或者估计出)模型里面的参数,在这个问题里就是 θ 0 \theta_{0} θ0和 θ 1 \theta_{1} θ1,求出参数后,就可以计算未知的房屋面积对应的房价了,因为只要带入这个公式即可求出对应房价。如果用图来说明,就是用一条线去拟合已有的样本数据,然后就可以求出未知的房屋面积在这条拟合的曲线上对应的房价值就ok了:
关键问题来了, 我们如何去求参数呢?使得我们建立的这个模型求出的 h θ h_{\theta } hθ(x)与真正的对应房价是拟合的或者说很接近,那就要使得 h θ h_{\theta } hθ(x)与真正的对应房价误差很小,那这个误差怎么表示呢?我们把这个误差称为Cost Function损失函数,这个时候就可以用梯度下降的算法来解决了!!!
因此,使用梯度下降算法就是为了求解模型中的参数问题,优化模型,使得模型更准确!误差更小!
2、如何衡量误差?——Cost Function损失函数
为了评估模型拟合的好坏,通常用损失函数(或者称为代价函数)来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。
损失函数的写法有好几种:
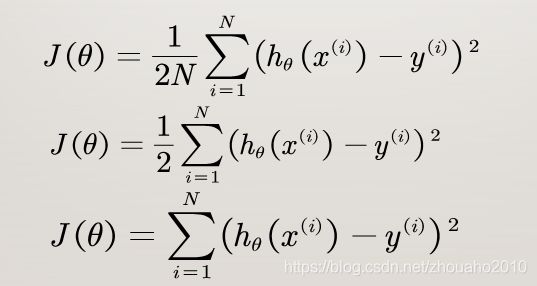
以上三种都是可以的,没有什么本质上的区别,具体写哪种要看具体的问题如何方便。本博文就采用第一种形式了,用均方误差的形式。
详细说明一下这个公式:
J(θ)就是损失函数,它代表假设函数 h θ h_{\theta } hθ(x)与样本实际输出y的误差大小,i代表第i个样本(一共有N个样本),x代表feature特征,上面那个房价问题就是指的是房屋面积,这里只有一个特征,也就是一个维度,那如果换多个feature的问题:
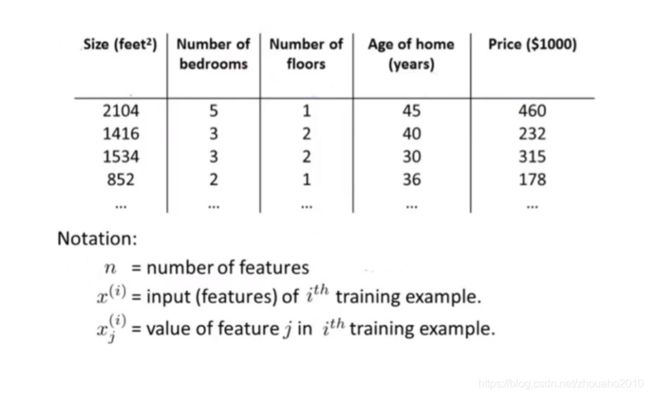 上面这张表中,房价有四个特征,即四个维度,即 x ( 1 ) x_{(1)} x(1)、 x ( 2 ) x_{(2)} x(2)、 x ( 3 ) x_{(3)} x(3)、 x ( 4 ) x_{(4)} x(4),如果再加上一个 x ( 0 ) x_{(0)} x(0),而且 x ( 0 ) x_{(0)} x(0)=1,那就是五个维度,那对应的参数θ就是5个,分别是 θ ( 0 ) θ_{(0)} θ(0)、 θ ( 1 ) θ_{(1)} θ(1)、 θ ( 2 ) θ_{(2)} θ(2)、 θ ( 3 ) θ_{(3)} θ(3)、 θ ( 4 ) θ_{(4)} θ(4),小写的n代表特征数,这里面n=4,实际维度就可以算为n+1=5个维度,那 x ( i ) x^{(i)} x(i)就代表第i个样本的特征集合,一般用向量表示,比如 x ( 2 ) x^{(2)} x(2)就是:
上面这张表中,房价有四个特征,即四个维度,即 x ( 1 ) x_{(1)} x(1)、 x ( 2 ) x_{(2)} x(2)、 x ( 3 ) x_{(3)} x(3)、 x ( 4 ) x_{(4)} x(4),如果再加上一个 x ( 0 ) x_{(0)} x(0),而且 x ( 0 ) x_{(0)} x(0)=1,那就是五个维度,那对应的参数θ就是5个,分别是 θ ( 0 ) θ_{(0)} θ(0)、 θ ( 1 ) θ_{(1)} θ(1)、 θ ( 2 ) θ_{(2)} θ(2)、 θ ( 3 ) θ_{(3)} θ(3)、 θ ( 4 ) θ_{(4)} θ(4),小写的n代表特征数,这里面n=4,实际维度就可以算为n+1=5个维度,那 x ( i ) x^{(i)} x(i)就代表第i个样本的特征集合,一般用向量表示,比如 x ( 2 ) x^{(2)} x(2)就是:
x ( 2 ) x^{(2)} x(2)= ( 1416 3 2 40 ) \begin{pmatrix} 1416\\ 3\\ 2\\ 40\end{pmatrix} ⎝⎜⎜⎛14163240⎠⎟⎟⎞
x j ( i ) {x_{j}}^{(i)} xj(i)则表示i个样本的第j个维度的特征值,如 x 1 ( 2 ) {x_{1}}^{(2)} x1(2)=1416, x 4 ( 4 ) {x_{4}}^{(4)} x4(4)=36,
首先我们先任意给各θ赋初值, h θ ( x ( i ) ) h_{\theta }(x^{(i)}) hθ(x(i))代表用我们假设的函数求出来第i样本对应的值(在这个问题就是房价), y ( i ) y^{(i)} y(i)代表第i个样本对应的实际的值(在这个问题里就是房价),如果用线性回归模型,则有:
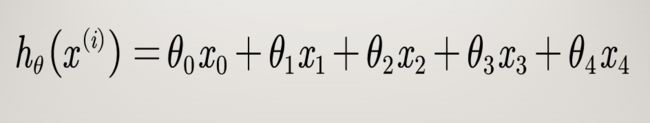
其中 x ( 0 ) x^{(0)} x(0)=1,那 θ ( 0 ) θ_{(0)} θ(0)就代表一个常数项,所以也可以写成:
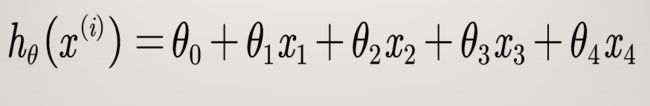
甚至我们写的更详细点,就是:
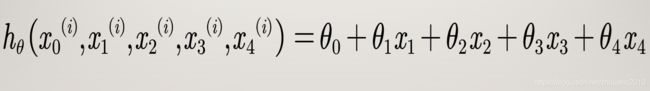 如果用矩阵的表达形式就是:
如果用矩阵的表达形式就是:
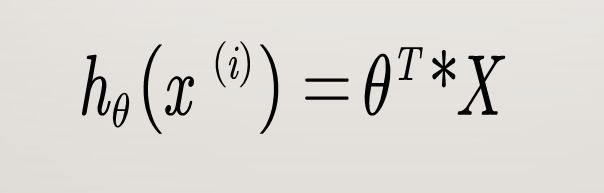
其中:
θ θ^{} θ= ( θ ( 0 ) θ ( 1 ) θ ( 2 ) θ ( 3 ) θ ( 4 ) ) \begin{pmatrix} θ_{(0)}\\ θ_{(1)}\\ θ_{(2)}\\ θ_{(3)}\\ θ_{(4)}\end{pmatrix} ⎝⎜⎜⎜⎜⎛θ(0)θ(1)θ(2)θ(3)θ(4)⎠⎟⎟⎟⎟⎞ , X X^{} X= ( x ( 0 ) x ( 1 ) x ( 2 ) x ( 3 ) x ( 4 ) ) \begin{pmatrix} x_{(0)}\\ x_{(1)}\\ x_{(2)}\\ x_{(3)}\\x_{(4)}\end{pmatrix} ⎝⎜⎜⎜⎜⎛x(0)x(1)x(2)x(3)x(4)⎠⎟⎟⎟⎟⎞ ,
(注:我为什么要把各种表达都写出来,就是因为不同的书籍、论文中写法不一样,我刚开始学习的时候就有各种疑惑,现在我都写出来就是各位初学者能学会各种表达形式,以免心存疑惑)
然后我们不断迭代更新θ,使得 h θ ( x ( i ) ) h_{\theta }(x^{(i)}) hθ(x(i))与 y ( i ) y^{(i)} y(i)的误差越来越小直至达到最小了(可能是0),那最后的θ就是我们所要求解的值。
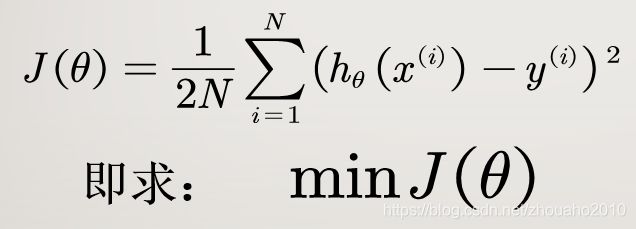
3、那如何求解参数θ使得损失函数J(θ)即误差最小呢?——梯度下降算法
3.1 什么是梯度
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。对于在点 ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0)的具体梯度向量就是(∂f/∂ x 0 x_{0} x0, ∂f/∂ y 0 y_{0} y0) T ^{T} T.或者▽f( ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0)),如果是3个参数的向量梯度,就是(∂f/∂x, ∂f/∂y,∂f/∂z) T ^{T} T,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点 ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0),沿着梯度向量的方向就是(∂f/∂ x 0 x_{0} x0, ∂f/∂ y 0 y_{0} y0) T ^{T} T的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂ x 0 x_{0} x0, ∂f/∂ y 0 y_{0} y0) T ^{T} T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
 所以所谓的“梯度”就是求偏导,“梯度下降”就是沿着“导数值”减小的方向(负梯度方向),这样就可使得损失函数快速减小,误差就减小。在机器学习算法中,在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。
所以所谓的“梯度”就是求偏导,“梯度下降”就是沿着“导数值”减小的方向(负梯度方向),这样就可使得损失函数快速减小,误差就减小。在机器学习算法中,在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。
3.2 梯度下降的场景假设
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来( 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
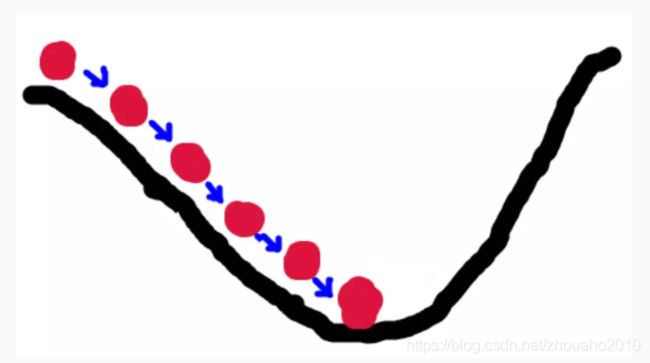
这里面的最低点也就是损失函数的最小值点,也就是误差最小值点,既然误差最小,那我们的模型就越拟合实际情况,那预测就越准确!
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。
3.3 微分
看待微分的意义,可以有不同的角度,最常用的两种是:
1、函数图像中,某点的切线的斜率
2、函数的变化率
几个微分的例子:
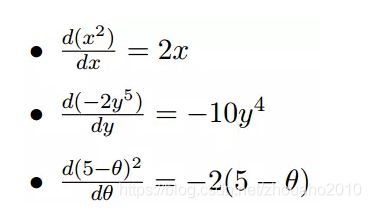
上面的例子都是单变量的微分,当一个函数有多个变量的时候,就有了多变量的微分,即分别对每个变量进行求微分:
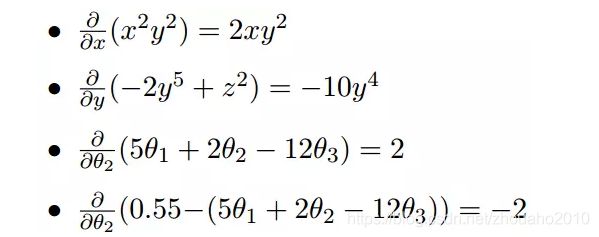
梯度实际上就是多变量微分的一般化:
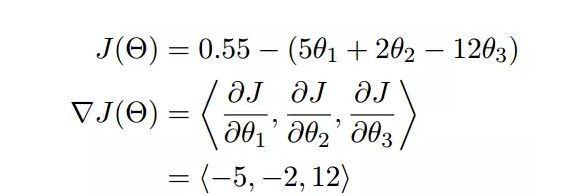
我们可以看到,梯度就是分别对每个变量进行微分,然后用逗号分割开,梯度是用<>包括起来,说明梯度其实一个向量。
梯度是微积分中一个很重要的概念,之前提到过梯度的意义
1、在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
2、在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
3.4 梯度下降算法的核心思想与详细步骤:
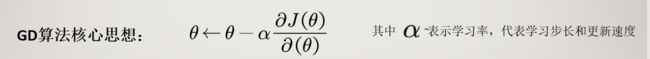
以二维为例,介绍如何求偏导!如图所示:
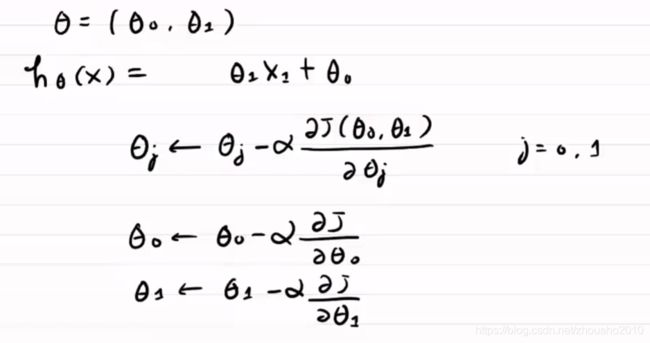 因为:
因为:
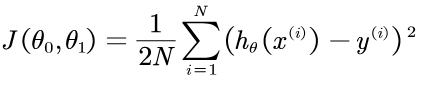
![]()
其中 x 0 x_{0} x0=1,则有:
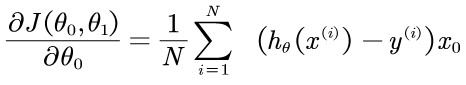
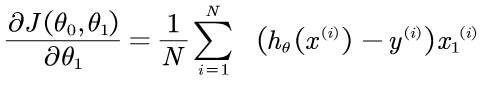
则一般化这个求偏导的公式为:
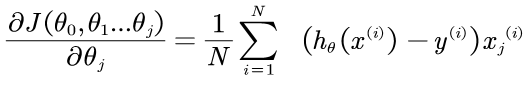
因此:

其中α为学习率,可以给定,然后修改,下面有详细的介绍。
注:如果看不懂这个公式请看我的视频讲解。
详细步骤:
1. 先决条件: 确认优化模型的假设函数和损失函数。
比如对于线性回归,假设函数表示为 :
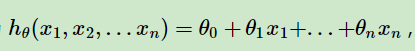
其中 θ i θ_{i} θi (i = 0,1,2… n)为模型参数, x i x_{i} xi(i = 0,1,2… n)为每个样本的n个特征值。为简化表示,我们增加一个特征 x 0 x_{0} x0=1 ,这样 h θ h_{θ} hθ( x 0 x_{0} x0, x 1 x_{1} x1,… x n x_{n} xn)= ∑ i = 0 n θ i x i \displaystyle\sum_{i=0}^{n} θ_ix_i i=0∑nθixi 。
同样是线性回归,对应于上面的假设函数,损失函数为:
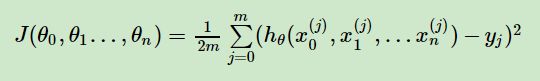
2、算法相关参数初始化。 主要是初始化θ0,θ1…,θn,算法终止距离ε以及步长(即学习率)α。在没有任何先验知识的时候,可以任意初始化,如将所有的θ初始化为0, 将步长(即学习率α)初始化为0.1。在调优的时候再优化。
关于学习率α,就是我2019年上半年参加一所高校博士招生考试的一道笔试题,我记得我答的比较准确,那么学习率该怎么取值呢?
学习率α就是步长,如果下山过程中,把梯度看做下山的方向,那学习率α就是每次走的步数,一般有两点考虑:  为便于大家理解,再举一个形象点的例子,假设地面有个坑,如果是大象过来,可以直接迈过那个坑了触碰不到坑的底端(错过了最优点),那如果是蚂蚁呢,那就可能磨磨唧唧要爬很多很多次才能到达坑的底端(算法非常慢甚至不能结束)。 所以学习率α不能过大也不能过小。
为便于大家理解,再举一个形象点的例子,假设地面有个坑,如果是大象过来,可以直接迈过那个坑了触碰不到坑的底端(错过了最优点),那如果是蚂蚁呢,那就可能磨磨唧唧要爬很多很多次才能到达坑的底端(算法非常慢甚至不能结束)。 所以学习率α不能过大也不能过小。
根据经验,可以从以下几个数值开始试验α的值,0.001 ,0.003, 0.01, 0.03, 0.1, 0.3, 1, …
α初始值为0.001, 不符合预期乘以3倍用0.003代替,不符合预期再用0.01替代,如此循环直至找到最合适的α。然后对于这些不同的 α 值,绘制J(θ)随迭代步数变化的曲线,然后选择看上去使得 J(θ)快速下降的一个 α 值。所以,在为梯度下降算法选择合适的学习速率α时,可以大致按3的倍数再按10的倍数来选取一系列α值
3. 算法过程。
1)确定当前位置的损失函数的梯度,对于θi,其梯度表达式如下:
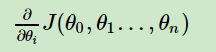
2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即:
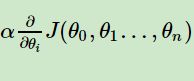
对应于前面下山例子中的某一步。
3)确定是否所有的θi,梯度下降的距离都小于ε,如果小于ε则算法终止,当前所有的θi(i=0,1,…n)即为最终结果。否则进入步骤4.
4)更新所有的θ,对于θi,其更新表达式如下。更新完毕后继续转入步骤1
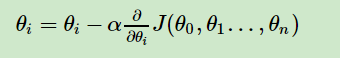
下面用线性回归的例子来具体描述梯度下降。假设我们的样本是:
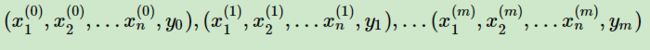
损失函数如前面所述:
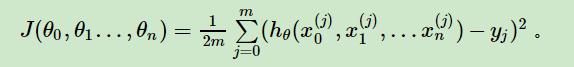
则在算法过程步骤1中对于θi 的偏导数计算如下(前面已经解释过了):
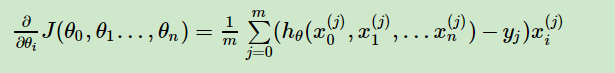
由于样本中没有 x 0 x_{0} x0,上式中令所有的 x 0 j x_{0}^{j} x0j=1.
步骤4中θi的更新表达式如下(前面已经解释过了):
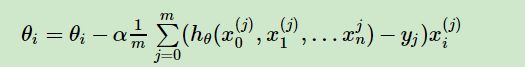
从这里可以看出当前点的梯度方向是由所有的样本决定的,加 1 m \frac{1}{m} m1是为了好理解。由于步长也为常数,他们的乘积也为常数,所以这里α 1 m \frac{1}{m} m1可以用一个常数表示。
4、梯度下降的算法调优
在使用梯度下降时,需要进行调优。哪些地方需要调优呢?
1. 算法的步长选择。在前面的算法描述中,我提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从小到大,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效,否则要增大步长。前面说了。步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
3.归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征x,求出它的期望x¯和标准差std(x),然后转化为:
5、改进的梯度下降的算法(大家族)
- 批量梯度下降法BGD(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新,这个方法就是前面讲的线性回归的梯度下降算法。
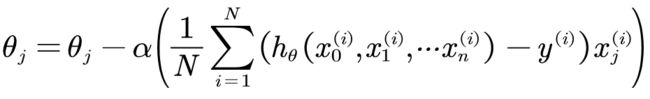
- 随机梯度下降法SGD(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的N个样本的数据,而是仅仅选取一个样本j来求梯度。对应的更新公式是:
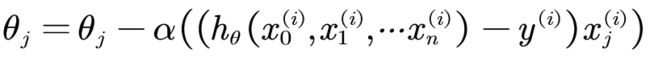
随机梯度下降法,和批量梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
那么,有没有一个中庸的办法能够结合两种方法的优点呢?有!这小批量梯度下降法MBGD。 - 小批量梯度下降法MBGD(Mini-batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于N个样本,我们采用x个样本来迭代,1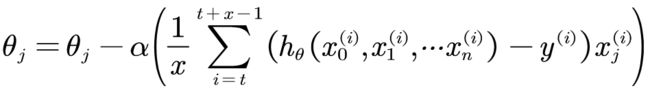
到此,梯度下降算法就全部讲完了,有些表达也参考了一些博文,在此表示感谢,大家看看如果有问题就留言。 熬夜写博客不容易啊,尤其是敲公式,这篇博文花了我好几天的时间不断修整,如果大家觉得有帮助,请点个赞、评论一下,非常感谢啊!你们的支持是我输出文章的极大鼓励!!!后面准备写代码实战!
视频讲解地址(直接点击即可)
如果有想要更快更容易了解梯度下降算法的童鞋请看我的视频讲解!制作视频花了很大心血,录错了又得重新来,反反复复花了很多时间,所以收取一点点费用,也是想赚点博士生活费,谢谢大家支持!
技术交流扣扣群:533209464(备注“学习”)