双指针 BFS问题分析+例题解析
文章目录
- 双指针
- 日志统计:
- 完全二叉树的权值
- BFS
- 献给啊尔吉依的花束
双指针
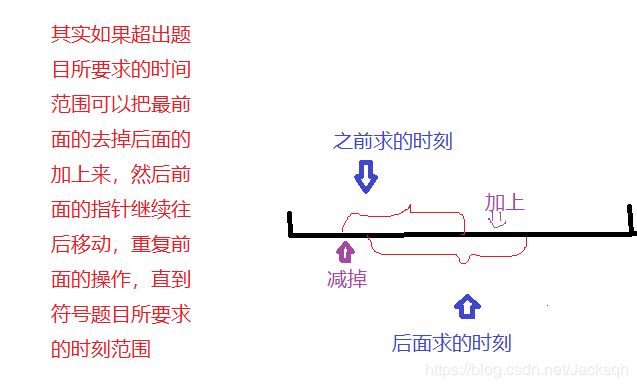
对于双指针,听着名字挺唬人,其实还好,在我的理解中双指针其实是一种思想:前后一起移动的i和j,按某些题目要求求一个范围内元素的总和(主要还是按题义来运用)
比如这一题
日志统计:
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N 行。
其中每一行的格式是:
ts id
表示在 ts 时刻编号 id 的帖子收到一个”赞”。
现在小明想统计有哪些帖子曾经是”热帖”。
如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞,小明就认为这个帖子曾是”热帖”。
具体来说,如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞,该帖就曾是”热帖”。
给定日志,请你帮助小明统计出所有曾是”热帖”的帖子编号。输入格式
第一行包含三个整数 N,D,K。
以下 N 行每行一条日志,包含两个整数 ts 和 id。输出格式
按从小到大的顺序输出热帖 id。
每个 id 占一行。
数据范围
1≤K≤N≤105,
0≤ts,id≤105,
1≤D≤10000
输入样例:
7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3
输出样例:
1
3
分析:这一题是要求在某个时间段内看某一篇文章的点赞数是否达到要求,如果达到要求就输出该文章的编号,这一题如果按平常的思路来看的话(一开始我的想法):把输入进来的时刻和编号进行保存,然后通过两重循环来遍历时间,看哪些文章满足条件,当然,这种方法也是可以的,但是这样的方法只是适用于小规模的数据而对于这一题来说的话是不行的。这一题的范围较大,必须要用O(n)或者O(nlogn)的做法做才不会超时,如果是按刚才的方法遍历的话会有O(n^2)的时间复杂度,会通过不了,这一题的思路是为了避免重复查询可以利用双指针来进行代码优化(一前一后,如果时间范围超过了前面的指针往后移)虽然还是对时间进行遍历但是这样的时间复杂度为O(n)
#include完全二叉树的权值
给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 A1,A2,···AN,如下图所示:
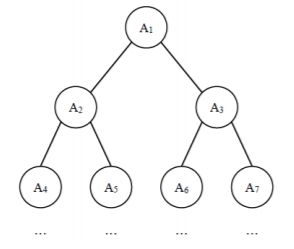
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?
如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1。输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,···AN。输出格式
输出一个整数代表答案。数据范围
1≤N≤105,
−105≤Ai≤105
输入样例:
7
1 6 5 4 3 2 1
输出样例:
2
分析:我做这一题的步骤是
- 找规律,并且了解完全二叉树的性质(最后一排不一定是全满的二叉树,其他排必须全满)
- 利用双指针来进行范围的取值(第一层是:1个元素 第二层是:2个元素…4,8,16)
- 最后一排结束的时候再赋值一次(我的一整套流程是满足个数再把值添加进去,避免最后一排个数不够(不满)再赋值一次最保险)
源码:
#include- 元素的取值是-105-105,在选择最大值的初始值时一定要小于它
- 如果元素很多或者元素很大的时候可能会爆int,最好用long
long来存结果
BFS
宽度优先搜索,一层一层的遍历,而我们知道的dfs是一条路走到黑(深度优先遍历)我们用bfs一般是拿来求一些最小距离之类的问题,dfs采用的数据结构是栈而bfs采用的则是队列(当然也有一些问题既可以用dfs也可以用bfs),在这还要说一下迷宫问题是bfs很重要的一个模型,下面举得例题基本上都是类似迷宫问题。
献给啊尔吉依的花束
阿尔吉侬是一只聪明又慵懒的小白鼠,它最擅长的就是走各种各样的迷宫。
今天它要挑战一个非常大的迷宫,研究员们为了鼓励阿尔吉侬尽快到达终点,就在终点放了一块阿尔吉侬最喜欢的奶酪。
现在研究员们想知道,如果阿尔吉侬足够聪明,它最少需要多少时间就能吃到奶酪。
迷宫用一个 R×C 的字符矩阵来表示。
字符 S 表示阿尔吉侬所在的位置,字符 E 表示奶酪所在的位置,字符 # 表示墙壁,字符 . 表示可以通行。
阿尔吉侬在 1 个单位时间内可以从当前的位置走到它上下左右四个方向上的任意一个位置,但不能走出地图边界。输入格式
第一行是一个正整数 T,表示一共有 T 组数据。
每一组数据的第一行包含了两个用空格分开的正整数 R 和 C,表示地图是一个 R×C 的矩阵。
接下来的 R 行描述了地图的具体内容,每一行包含了 C 个字符。字符含义如题目描述中所述。保证有且仅有一个 S 和 E。输出格式
对于每一组数据,输出阿尔吉侬吃到奶酪的最少单位时间。
若阿尔吉侬无法吃到奶酪,则输出“oop!”(只输出引号里面的内容,不输出引号)。
每组数据的输出结果占一行。数据范围
1
3
3 4
.S..
###.
..E.
3 4
.S..
.E..
....
3 4
.S..
####
..E.
输出样例:
5
1
oop!
#include