(线段树)求区间最大连续子段和
https://www.acwing.com/problem/content/246/
题解:某大佬的区间子段和的解释:https://blog.csdn.net/wu_tongtong/article/details/73385029
线段树需要维护的是:
[x,y]内的最大子段和 ms
[x,y]的区间和 s
[x,y]内的紧靠左端点的最大子段和 ls
[x,y]内的紧靠右端点的最大子段和 rs
s的维护很常规,
ls:有两种情况:
1.该区间内的ls是ta左儿子的ls
2.该区间内的ls是左儿子的s+右儿子的ls
同理,rs:有两种情况:
1.该区间内的rs是ta右儿子的rs
2.该区间内的rs是右儿子的s+左儿子的rs
而ms有三种情况:
1.该区间内的ms是左儿子的ms
2.该区间内的ms是右儿子的ms
3.该区间内的ms是左儿子的rs+右儿子的ls
---------------------
作者:Coco_T_
来源:CSDN
原文:https://blog.csdn.net/wu_tongtong/article/details/73385029
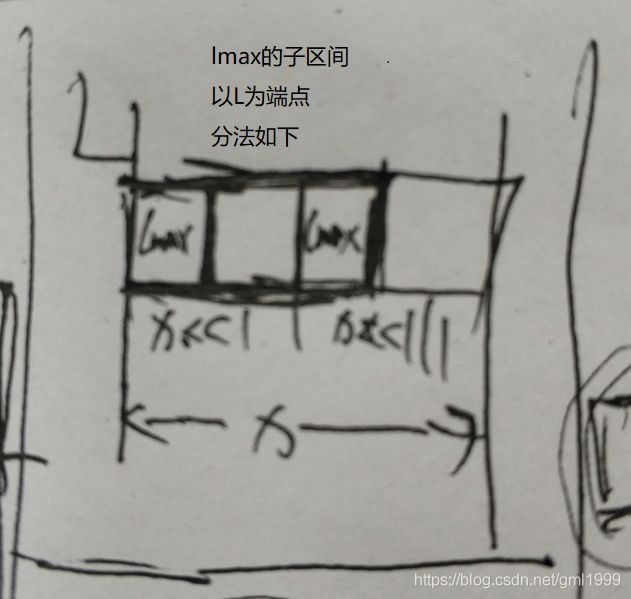
版权声明:本文为博主原创文章,转载请附上博文链接!所以线段树维护区间和sum,以L为端点紧靠L的最大和lmax,以R为端点的紧靠R的子段和rmax,以及区间最大子段和lrs
例如: lmax:
tree[x].lmax=max(tree[x<<1].lmax , tree[x<<1|1].lmax+tree[x<<1].sum);1.该区间内的lmax是ta左儿子的lmax
2.该区间内的lmax是左儿子的sum+右儿子的lmax
#include
#include
#include
#include
#include
#include
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=1000000;
typedef long long ll;
struct node{
ll sum;
ll lmax;//以L为端点的 紧靠L的区间
ll rmax;//以R为端点的 紧靠R的区间
ll lrs; //区间[L,R]的最大和
}tree[maxn*4];
//int a[maxn];
void pushup(int x){
tree[x].sum=tree[x<<1].sum+tree[x<<1|1].sum;
tree[x].lmax=max(tree[x<<1].lmax , tree[x<<1|1].lmax+tree[x<<1].sum);
tree[x].rmax=max(tree[x<<1|1].rmax , tree[x<<1].rmax+tree[x<<1|1].sum);
tree[x].lrs=max(max(tree[x<<1].lrs,tree[x<<1|1].lrs) , tree[x<<1].rmax+tree[x<<1|1].lmax);
}
void build(int l,int r,int p){
if(l==r){
cin>>tree[p].sum;
tree[p].lmax=tree[p].lrs=tree[p].rmax=tree[p].sum;
return ;
}
int mid=(l+r)/2;
build(l,mid,p<<1);
build(mid+1,r,p<<1|1);
pushup(p);
}
void update(int k,int v,int l,int r,int p){
if(l==r){
tree[p].lmax=tree[p].lrs=tree[p].rmax=tree[p].sum=v;
return ;
}
int mid=(l+r)/2;
if(k<=mid){
update(k,v,l,mid,p<<1);
}else{
update(k,v,mid+1,r,p<<1|1);
}
pushup(p);
}
node quert(int L,int R,int l,int r,int p){
if(L<=l&&r<=R){
return tree[p];
}
int mid=(l+r)/2;
node vis;
node f1;
node f2;
vis.sum=0;
if(L<=mid){
f1=quert(L,R,l,mid,p<<1);
vis=f1;
}
if(R>mid){
f2=quert(L,R,mid+1,r,p<<1|1);
vis=f2;
}
if(L<=mid&&R>mid){//一段区间被拆开两部分 需要合起来再判断一下;
vis.sum=f1.sum+f2.sum;
vis.lmax=max(f1.lmax,f1.sum+f2.lmax);
vis.rmax=max(f2.rmax,f2.sum+f1.rmax);
vis.lrs=max(max(f1.lrs,f2.lrs),f1.rmax+f2.lmax);
}
return vis;
}
int main(){
int n,m;
cin>>n>>m;
build(1,n,1);
while(m--){
int k,x,y;
cin>>k>>x>>y;
if(k==1){
if(x>y) swap(x,y);
node ans=quert(x,y,1,n,1);
cout<