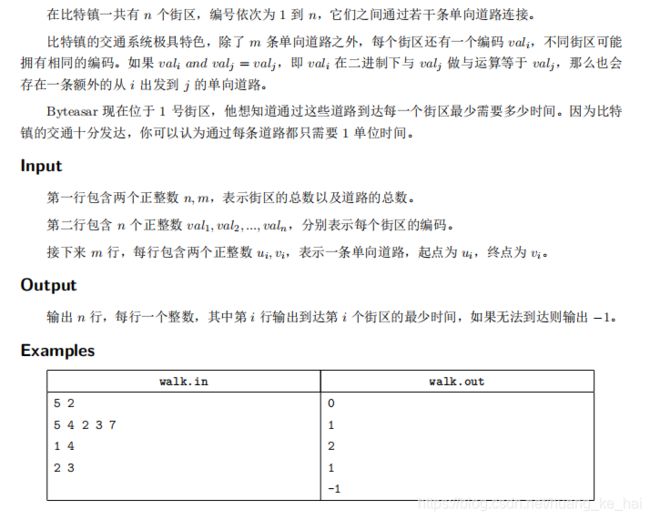
【题解 && 建图技巧】 比特漫步

题目描述：

---

Solution

40pts：

直接按照题意建图跑最短路即可。
Tips:题目要求的边都是单向边

---

70pts：

如果直接按照题意$n^2$建边，很显然会超时。
我们发现$val$最多只有$2^{20}$个，而建边的条件即$i->j(va{l}_j\in va{l}_i)$。
因此，我们可以将第$i$号点向他的$va{l}_i$连一条长度为0的边，$va{l}_i$ 向i连一条长度为1的边。
不仅如此，对于每个$k(k\in 2^{20})$，我们将$k$向k的子集连一条长度为0的边。
经过这样的建图，我们做最短路（或者BFS）就可以满足题目要求。（中间可以不断操作，当到达一个点时就会有1的代价，即从一个点走到另一个点）

Code

#include
using namespace std;

const int  N = 20010000;
int n,m;
struct Node{
	int y,Next,v;
}e[2*N];
int val[N];
int dis[N];
bool vi[N];
int len = 0 , linkk[N ];

void Insert(int x,int y,int v){
	e[++len].Next = linkk[x];
	linkk[x] = len;
	e[len].y = y;
	e[len].v = v;
}

int main(){
	freopen("walk.in","r",stdin);
	freopen("walk.out","w",stdout);
	scanf("%d %d",&n,&m);
	int A = n+1;
	int maxx = 0;
	for (int i = 1; i <= n; i++){
		scanf("%d",&val[i]);
		maxx = max(maxx,val[i]);
		Insert(i,val[i]+A , 0);
		Insert(val[i]+A , i , 1);//连边
	}
	for (int i = 1; i <= maxx; i++)
	  	  for (int j = 0; j <= 20; j++)
	  	    if (i & (1<<j)) Insert(i+A , (i ^ (1<<j))+A , 0);
	for (int i = 1,x,y; i <= m; i++) scanf("%d %d",&x,&y) , Insert(x,y,1);
	queue < int > q;
	memset(vi,0,sizeof vi);
	memset(dis,40,sizeof dis);
	dis[1] = 0; q.push(1);vi[1] = 1;
	while (!q.empty()){
		int x = q.front(); vi[x] = 0;q.pop();
		for (int i = linkk[x]; i; i = e[i].Next){
			int y = e[i].y , v = e[i].v;
			if (dis[y] > dis[x] + v){
				dis[y] = dis[x] + v;
				if (!vi[y]) q.push(y) , vi[y] = 1;
			}
		}
	}
	for (int i = 1; i <= n; i++) printf("%d\n",dis[i] > 10000000?-1:dis[i]);
	return 0;
}

---

100pts

我们如果直接按照70pts 的方法建图，就会MLE，我们考虑优化空间。
我们其实没必要将每个点的子集都连边，只需要将需要的边和点连接即可。
因此，我们放弃之前的预处理，在做BFS的时候，每做完一个点$x$，就枚举$x$的子集，用$x$来更新$x$的子集，这样就可以将每一个空间都利用起来，即满分做法。

Code

#include
using namespace std;

const int  N = 20010000;
int n,m;
struct Node{
	int y,Next,v;
}e[2*N];
int val[N];
int dis[N];
bool vi[N];
int len = 0 , linkk[N ];

void Insert(int x,int y,int v){
	e[++len].Next = linkk[x];
	linkk[x] = len;
	e[len].y = y;
	e[len].v = v;
}

int main(){
	freopen("walk.in","r",stdin);
	freopen("walk.out","w",stdout);
	scanf("%d %d",&n,&m);
	int A = n+1;
	int maxx = 0;
	for (int i = 1; i <= n; i++){
		scanf("%d",&val[i]);
		maxx = max(maxx,val[i]);
		Insert(i,val[i]+A , 0);
		Insert(val[i]+A , i , 1);
	    vi[val[i]] = 1;
	}
//	for (int i = 1; i <= maxx; i++)
//	  if (vi[i]){
//	  	  for (int j = 0; j <= 20; j++)
//	  	    if (i & (1<
//	  }
	for (int i = 1,x,y; i <= m; i++) scanf("%d %d",&x,&y) , Insert(x,y,1);
	queue < int > q;
	memset(vi,0,sizeof vi);
	memset(dis,40,sizeof dis);
	dis[1] = 0; q.push(1);vi[1] = 1;
	while (!q.empty()){
		int x = q.front(); vi[x] = 0;q.pop();
		for (int i = linkk[x]; i; i = e[i].Next){
			int y = e[i].y , v = e[i].v;
			if (dis[y] > dis[x] + v){
				dis[y] = dis[x] + v;
				if (!vi[y]) q.push(y) , vi[y] = 1;
			}
		}
		if (x > n){
			x-=A;
			for (int i = 0; i <= 20; i++)
			  if (x&(1<<i)){
			  	  int y = x ^ (1<<i);
			  	  if (dis[y+A] > dis[x+A]){
			  	  	  dis[y+A] = dis[x+A];
			  	  	  if (!vi[y+A]) q.push(y+A) , vi[y+A] = 1;
			  	  }
			  }
		}
	}
	for (int i = 1; i <= n; i++) printf("%d\n",dis[i] > 100000000?-1:dis[i]);
	return 0;
}