【生成函数】五边形数定理与整数划分问题详解
Part 0. 前置知识
- 简单的公式推导
- 生成函数
大量数学公式警告
Part 1. 什么是五边形数
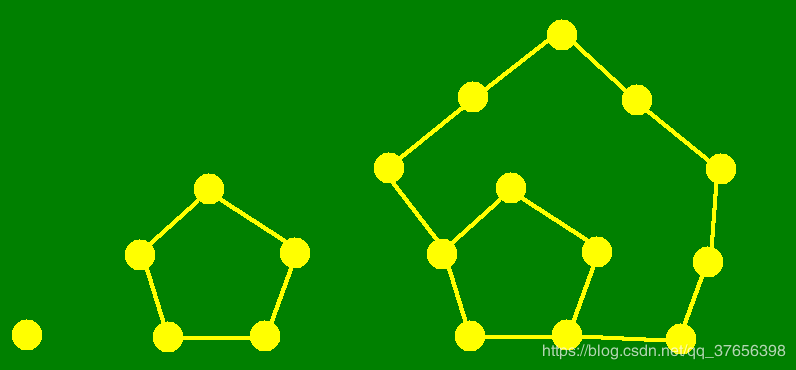
五边形数
XP 系统带的画图真的挺好用!
我们不难得出五边形数的数列:
P = { 1 , 5 , 12 , 22 , … } P = \{1, 5, 12, 22,\ldots\} P={1,5,12,22,…}
再找一下规律,我们就可以得到五边形数的通项公式:
P n = n ( 3 n − 1 ) 2 P_n = \frac{n(3n - 1)}{2} Pn=2n(3n−1)
似乎现在并没有什么用。。。
广义五边形数
也就是当 n n n 可以为负数的时候的五边形数序列,它的通项公式为:
P n = n ( 3 n ± 1 ) 2 P_n = \frac{n(3n \pm 1)}{2} Pn=2n(3n±1)
Part 2. 五边形数定理
定义欧拉函数(注意不要把它看成数论里面的欧拉函数)为:
ϕ ( n ) = ∏ i = 1 ∞ ( 1 − x i ) \phi (n) = \prod\limits_{i = 1}^{\infty} (1 - x^i) ϕ(n)=i=1∏∞(1−xi)
则五边形数定理就是:
ϕ ( n ) = ∏ i = − ∞ ∞ ( − 1 ) i x i ( 3 i − 1 ) 2 = 1 + ∏ i = 0 ∞ ( − 1 ) i x i ( 3 i ± 1 ) 2 \phi (n) = \prod\limits_{i = -\infty}^{\infty}(-1)^ix^{\frac{i(3i - 1)}{2}} = 1 + \prod\limits_{i = 0}^{\infty}(-1)^ix^{\frac{i(3i \pm 1)}{2}} ϕ(n)=i=−∞∏∞(−1)ix2i(3i−1)=1+i=0∏∞(−1)ix2i(3i±1)
证明等一会给出。
Part 3. Ferrers 图
Ferrers 图是一个由 k k k 行的点阵构成的方格图,要求上一行的格子数目不超过它下面一行的格子的数目,其中总和为 n n n 的数量。
举个例子:( n = 20 n = 20 n=20 时 的一个图,我用 @ 来表示一个格子)
@@@@@@
@@@@@
@@@@
@@@
@@
我们记这时的第 k k k 行的格子数量为 m m m, s s s 为第一行最右边的 @ 右上角的对角线格子数量。
定义一种变换:
- 当 m > s m > s m>s 时, 把最右边的对角线上的格子扔到新的一行。
- 当 m ≤ s m \le s m≤s 时,把最后一行的所有格子分给从第一行开始的每行上,每行分到一个格子。
举个例子:(用 $ 表示被移走的格子)
@@@@@@@@ @@@@@@@@$
@@@@@@@ @@@@@@@$
@@@@@ <=> @@@@@
@@@ @@@
$$
不难看出这个操作是显然可逆的。
这个操作还有一些性质:
我们对一个 Ferrers 图进行连续的两次变换后,它会变回它本身。
如果我们仅进行一次变换,那么行数的奇偶性可以改变。
Part 4. 五边形数定理的证明
我们将 ϕ ( n ) \phi(n) ϕ(n) 的定义式展开之后可以发现,第 n n n 项的系数应该是将 n n n 划分成偶数个互不相同的正整数的答案减掉将 n n n 划分成奇数个互不相同的正整数方案,每一项的系数应该都是 0 0 0。但实际操作后发现有些项前面是有系数的。
那么我们考虑仔细研究一下 Ferrers 图。
当 m = s + 1 m = s + 1 m=s+1 时,且底层的最右边的元素与对角线相遇,如下:
@@@@@@ @@@@@
@@@@@ => @@@@
@@@@ @@@
@@@
发现此时无法操作回去了。这是一个不合法的状态。
令 t = 1 − m t = 1 - m t=1−m,可以得到 n = ( 1 − t ) + ( 2 − t ) + ( 3 − t ) + ⋯ + ( − 2 t ) = t ( 3 t − 1 ) 2 n = (1 - t) + (2 - t) + (3 - t) + \cdots + (-2t) = \frac{t(3t - 1)}{2} n=(1−t)+(2−t)+(3−t)+⋯+(−2t)=2t(3t−1),这一项对答案的贡献为 ( − 1 ) t (-1) ^ t (−1)t。
当 m = s m = s m=s,且底层的最右边的元素与对角线相遇,如下:
@@@@@ @@@@@@
@@@@ => @@@@@
@@@ @
这个显然是不合法的,令 t = m t = m t=m,可以得到 n = t + ( t + 1 ) + ( t + 2 ) + ⋯ + 2 t = t ( 3 t + 1 ) 2 n = t + (t + 1) + (t + 2) + \cdots + 2t = \frac{t(3t + 1)}{2} n=t+(t+1)+(t+2)+⋯+2t=2t(3t+1),对第 n n n 项的贡献为 ( − 1 ) t (-1) ^ t (−1)t。
这样一来,当 n = k ( 3 k ± 1 ) 2 n = \frac{k(3k \pm 1)}{2} n=2k(3k±1) 时,即 n n n 是一个广义五边形数时, n n n 的奇偶拆分就在抵消之后留下一项。所以五边形定理成立。
Part 5. 整数划分问题
问题概要
将一个整数 n n n 划分成任意个可以相等的整数,求方案数。
分析
我们不难写出一个 O ( n 2 ) O(n^2) O(n2) 的 DP 来解决整数划分问题。但当 n n n 超过 1 0 4 10^4 104 之后就跑不动了。
考虑高效解法 (利用五边形数定理)
定义函数 P ( i ) P(i) P(i) 为将 n n n 拆分成若干个可以相等的整数的方案数。
考虑 P ( i ) P(i) P(i) 的生成函数 F ( x ) F(x) F(x):
F ( x ) = ∑ i = 1 ∞ P ( i ) x i = ∏ i = 1 ∞ ( x 0 + x i + x 2 i + ⋯ ) = ∏ i = 1 ∞ 1 1 − x i \begin{aligned} F(x) & = \sum\limits_{i = 1}^{\infty}P(i)x^i \\ &= \prod\limits_{i = 1}^{\infty}(x^0 + x^i + x^{2i} + \cdots) \\ & =\prod\limits_{i = 1}^{\infty} \frac{1}{1 - x^i} \end{aligned} F(x)=i=1∑∞P(i)xi=i=1∏∞(x0+xi+x2i+⋯)=i=1∏∞1−xi1
再看一下上面提到的欧拉函数:
ϕ ( x ) = ∏ i = 1 ∞ ( 1 − x i ) \phi(x) = \prod\limits_{i = 1}^{\infty} (1 - x^i) ϕ(x)=i=1∏∞(1−xi)
显然可以得到: F ( x ) ⋅ ϕ ( x ) = 1 F(x)\cdot\phi(x) = 1 F(x)⋅ϕ(x)=1。
然后根据五边形数定理将 ϕ ( x ) \phi(x) ϕ(x) 代入:
[ ∑ i = 1 ∞ P ( i ) x i ] ⋅ ( ∑ i = 0 ∞ 1 + ∏ i = 0 ∞ ( − 1 ) i x i ( 3 i ± 1 ) 2 ) = 1 \left[\sum\limits_{i = 1}^{\infty}P(i)x^i\right] \cdot \left(\sum\limits_{i = 0}^{\infty}1 + \prod\limits_{i = 0}^{\infty}(-1)^ix^{\frac{i(3i \pm 1)}{2}}\right) = 1 [i=1∑∞P(i)xi]⋅(i=0∑∞1+i=0∏∞(−1)ix2i(3i±1))=1
直接暴力展开可以得到:
P ( n ) − P ( n − 1 ) − P ( n − 2 ) + P ( n − 5 ) + P ( n − 7 ) − ⋯ = 0 P(n) - P(n - 1) - P(n - 2) + P(n - 5) + P(n - 7) - \cdots = 0 P(n)−P(n−1)−P(n−2)+P(n−5)+P(n−7)−⋯=0
不难发现减去的每一项都是广义五边形数。于是直接暴力计算即可。
由于五边形数 p n = n ( 3 n ± 1 ) 2 p_n = \frac{n(3n \pm 1)}{2} pn=2n(3n±1) 的增长速度为 O ( n 2 ) O(n ^ 2) O(n2)。所以最多枚举不超过 O ( n ) O(\sqrt n) O(n) 项五边形数就可以退出循环,故时间复杂度为 O ( n n ) O(n\sqrt n) O(nn)。
Part 6. 例题
HDU 4651
题目大意
求将正整数 n n n 划分成多个正整数的和的方案数。
分析
就是一个模板了。。。好好看一看上面的就可以了。
HDU 4658
题目大意
将一个正整数 n n n 划分为多个正整数的和的方案数,但每个数的使用次数不能够大于等于 k k k 次。
分析
记这种方式下的划分数为 P ′ ( n ) P'(n) P′(n)。先给出生成函数 G ( x ) = ∏ i = 1 ∞ ( 1 + x i + x 2 i + ⋯ + x ( k − 1 ) i ) G(x) = \prod\limits_{i = 1}^{\infty}(1 + x^i + x^{2i} + \cdots + x^{(k - 1)i}) G(x)=i=1∏∞(1+xi+x2i+⋯+x(k−1)i)。
尝试化简:
G ( x ) = ∏ i = 1 ∞ 1 + x i + x i + x i + ⋯ 1 + x k i + x 2 k i + x 3 k i + ⋯ = ∏ i = 1 ∞ 1 1 − x i 1 1 − x k i = ∏ i = 1 ∞ 1 − x k i 1 − x i = ϕ ( x k ) ϕ ( x ) = ϕ ( x k ) ⋅ F ( x ) \begin{aligned} G(x) & = \prod\limits_{i = 1}^{\infty}\frac{1+ x^i + x^i + x^i + \cdots}{1 + x^{ki} + x^{2ki} + x^{3ki} + \cdots} \\ & = \prod_{i = 1}^{\infty}\frac{\frac{1}{1 - x^i}}{\frac{1}{1 - x^{ki}}} \\ & = \prod_{i = 1}^{\infty}\frac{1 - x^{ki}}{1 - x^i} \\ & = \frac{\phi(x^k)}{\phi(x)} \\ & = \phi(x^k) \cdot F(x) \end{aligned} G(x)=i=1∏∞1+xki+x2ki+x3ki+⋯1+xi+xi+xi+⋯=i=1∏∞1−xki11−xi1=i=1∏∞1−xi1−xki=ϕ(x)ϕ(xk)=ϕ(xk)⋅F(x)
然后暴力展开 ϕ ( x k ) ⋅ F ( x ) \phi(x^k) \cdot F(x) ϕ(xk)⋅F(x) 得到:
∑ i = 1 ∞ P ′ ( i ) x i = ( 1 − x k − x 2 k + x 5 k + ⋯ ) [ 1 + P ( 1 ) x + P ( 2 ) x 2 + ⋯ ] \sum\limits_{i = 1}^{\infty}P'(i)x^i = (1 - x^k - x^{2k} + x^{5k} + \cdots)[1 + P(1)x + P(2)x^2 + \cdots] i=1∑∞P′(i)xi=(1−xk−x2k+x5k+⋯)[1+P(1)x+P(2)x2+⋯]
然后可以得到 P ′ ( i ) = P ( i ) − P ( i − k ) − P ( i − 2 k ) + P ( i − 5 k ) + ⋯ P'(i) = P(i) - P(i - k) - P(i - 2k) + P(i - 5k) + \cdots P′(i)=P(i)−P(i−k)−P(i−2k)+P(i−5k)+⋯
于是就可以在 O ( n ) O(\sqrt n) O(n) 的时间内回答询问了,总时间复杂度为 O ( n n + T n ) O(n\sqrt n + T\sqrt n) O(nn+Tn)。
参考代码
HDU 4651
#include HDU 4658
#include