【DP】四边形不等式优化详解(二)
Part.3 如何证明 w ( l , r ) w(l, r) w(l,r) 满足四边形不等式
其实四边形不等式优化的最重要、最关键、也是最开始的一步就是证明 w ( l , r ) w(l, r) w(l,r) 满足四边形不等式。
我们发现直接用定义来证明来证某些 w ( l , r ) w(l, r) w(l,r) 其实是不好做的。
推论: 若对于 a < b a < b a<b 有 w ( a + 1 , b + 1 ) + w ( a , b ) ≤ w ( a + 1 , b ) + w ( a , b + 1 ) w(a + 1, b + 1) + w(a, b) \le w(a + 1, b) + w(a, b+ 1) w(a+1,b+1)+w(a,b)≤w(a+1,b)+w(a,b+1),则 w ( l , r ) w(l, r) w(l,r) 满足四边形不等式。
证明: 当 a < c a < c a<c 时,根据推论可得:
w ( a , c ) + w ( a + 1 , c + 1 ) ≤ w ( a + 1 , c ) + w ( a , c + 1 ) w(a, c) + w(a + 1, c + 1) \le w(a + 1, c) + w(a, c + 1) w(a,c)+w(a+1,c+1)≤w(a+1,c)+w(a,c+1)
当 a + 1 < c a + 1 < c a+1<c 时,有:
w ( a + 1 , c ) + w ( a + 2 , c + 1 ) ≤ w ( a + 1 , c + 1 ) + w ( a + 2 , c ) w(a + 1, c) + w(a + 2, c + 1) \le w(a + 1, c + 1) + w(a + 2, c) w(a+1,c)+w(a+2,c+1)≤w(a+1,c+1)+w(a+2,c)
两不等式相加并整理得到:
w ( a , c ) + w ( a + 2 , c + 1 ) ≤ w ( a , c + 1 ) + w ( a + 2 , c ) w(a, c) + w(a + 2, c + 1) \le w(a, c + 1) + w(a + 2, c) w(a,c)+w(a+2,c+1)≤w(a,c+1)+w(a+2,c)
由此类推,对于任意的 a ≤ b ≤ c a \le b \le c a≤b≤c 有:
w ( a , c ) + w ( b , c + 1 ) ≤ w ( a , c + 1 ) + w ( b , c ) w(a, c) + w(b, c + 1) \le w(a, c + 1) + w(b, c) w(a,c)+w(b,c+1)≤w(a,c+1)+w(b,c)
用同样的方法可以得到:对于任意的 a ≤ b ≤ c ≤ d a \le b \le c \le d a≤b≤c≤d 有:
w ( a , c ) + w ( b , d ) ≤ w ( a , d ) + w ( b , c ) w(a, c) + w(b, d) \le w(a, d) + w(b, c) w(a,c)+w(b,d)≤w(a,d)+w(b,c)
这里给出几个 简单的 例子来帮助理解如何证明 w ( l , r ) w(l, r) w(l,r) 是满足四边形不等式的。
Part.3/1 或
状态转移方程:(其中 w ( i , j ) w(i, j) w(i,j) 表示从位置 i i i 到位置 j j j 的元素的或)
f ( i ) = max j = 1 i − 1 { f ( j ) + w ( j , i ) } f(i) = \max\limits_{j = 1}^{i - 1}\{f(j) + w(j, i)\} f(i)=j=1maxi−1{f(j)+w(j,i)}
我们要证明的是对于任意两个位置 a , b ( a < b ) a, b(a < b) a,b(a<b) 有 w ( a + 1 , b + 1 ) + w ( a , b ) ≤ w ( a + 1 , b ) + w ( a , b + 1 ) w(a + 1, b + 1) + w(a, b) \le w(a + 1, b) + w(a, b + 1) w(a+1,b+1)+w(a,b)≤w(a+1,b)+w(a,b+1)
不难发现或运算对于每一位都是独立的。所以我们将 w ( l , r ) w(l, r) w(l,r) 按二进制位拆成 w ′ ( l , r ) w'(l, r) w′(l,r),于是我们只需要证明 w ′ ( l , r ) w'(l, r) w′(l,r) 满足四边形不等式即可。
由或运算的性质显然可以看出 w ′ ( l , r ) w'(l, r) w′(l,r) 是满足区间包含单调性的,接下来说明它满足四边形不等式。
对于区间 [ a + 1 , b ] [a + 1, b] [a+1,b] 中的二进制位上的 0 1 情况,我们分类讨论:
情况(1): 当这段区间上的所有位置都为 0 0 0 时,我们再分成三种情况讨论:
-
情况(1-1): a a a 位置上为 0 0 0, b + 1 b + 1 b+1 位置上为 0 0 0:显然 w ( a + 1 , b + 1 ) = 0 , w ( a , b ) = 0 , w ( a + 1 , b ) = 0 , w ( a , b + 1 ) = 0 w(a + 1, b + 1) = 0, w(a, b) = 0, w(a + 1, b) = 0, w(a, b + 1) = 0 w(a+1,b+1)=0,w(a,b)=0,w(a+1,b)=0,w(a,b+1)=0,显然成立。
-
情况(1-2): a a a 位置上为 1 1 1, b + 1 b + 1 b+1 位置上为 1 1 1:可以得到 w ( a + 1 , b + 1 ) = 1 , w ( a , b ) = 0 , w ( a + 1 , b ) = 0 , w ( a , b + 1 ) = 1 w(a + 1, b + 1) = 1, w(a, b) = 0, w(a + 1, b) = 0, w(a, b + 1) = 1 w(a+1,b+1)=1,w(a,b)=0,w(a+1,b)=0,w(a,b+1)=1,显然成立。
-
情况(1-3): a a a 位置上为 0 0 0, b + 1 b + 1 b+1 位置上为 1 1 1 或者 a a a 位置上为 1 1 1, b b b 位置上为 0 0 0:可以得到: w ( a + 1 , b + 1 ) = 0 , w ( a , b ) = 0 w(a + 1, b + 1) = 0, w(a, b) = 0 w(a+1,b+1)=0,w(a,b)=0 或者 1 , w ( a + 1 , b ) = 0 , w ( a , b + 1 ) = 1 1, w(a + 1, b) = 0, w(a, b + 1) = 1 1,w(a+1,b)=0,w(a,b+1)=1 或者 0 0 0。仍然成立。
情况(2): 这段区间上所有的位置有至少一个 1 1 1,那么有 w ( a + 1 , b + 1 ) = 1 , w ( a + 1 , b + 1 ) = 1 , w ( a , b ) = 1 , w ( a + 1 , b ) = 1 , w ( a , b + 1 ) = 1 w(a + 1, b + 1) = 1, w(a + 1, b + 1) = 1, w(a, b) = 1, w(a + 1, b) = 1, w(a, b + 1) = 1 w(a+1,b+1)=1,w(a+1,b+1)=1,w(a,b)=1,w(a+1,b)=1,w(a,b+1)=1,显然成立。
综上, w ( l , r ) w(l, r) w(l,r) 满足四边形不等式。故 f ( i ) f(i) f(i) 也满足四边形不等式,故可以用四边形不等式优化到 O ( N log 2 N ) O(N \log_2 N) O(Nlog2N)。
Part.3/2 最大值
w ( l , r ) w(l, r) w(l,r) 表示区间 [ l , r ] [l, r] [l,r] 的最大值。
考虑直接用定义证明 w ( i , j ) w(i, j) w(i,j) 满足四边形不等式。
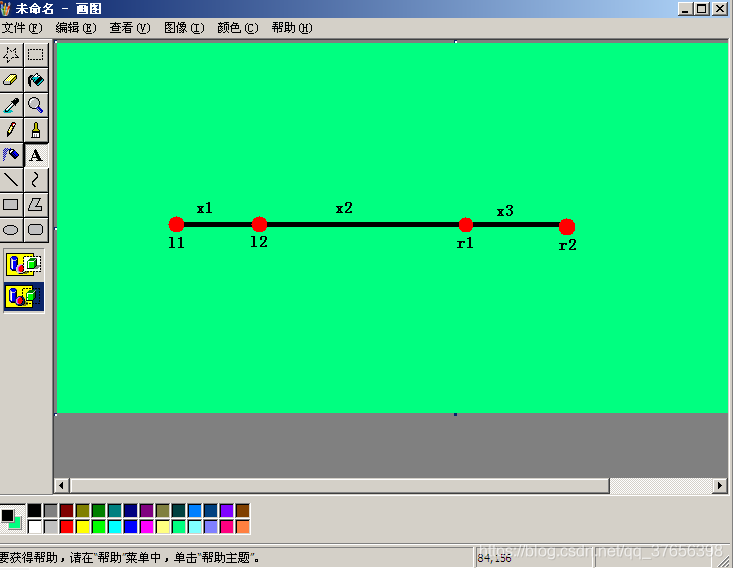
我们任取 a ≤ b ≤ c ≤ d a \le b \le c \le d a≤b≤c≤d,并记区间 [ a , b ) [a, b) [a,b) 上的最大值为 x 1 x_1 x1,区间 [ b , c ] [b, c] [b,c] 上的最大值为 x 2 x_2 x2,区间 ( c , d ] (c, d] (c,d] 上的最大值为 x 3 x_3 x3。
那么 w ( a , c ) + w ( b , d ) = max ( x 1 , x 2 ) + max ( x 2 , x 3 ) , w ( a , d ) + w ( b , c ) = x 2 + max ( x 1 , x 2 , x 3 ) w(a, c) + w(b, d) = \max(x_1, x_2) + \max(x_2, x_3),w(a, d) + w(b, c) = x_2 + \max(x_1, x_2, x_3) w(a,c)+w(b,d)=max(x1,x2)+max(x2,x3),w(a,d)+w(b,c)=x2+max(x1,x2,x3)。
就像这样:
(由于我的操作失误,请自动将 l1 视为 a a a,l2 视为 b b b,r1 视为 c c c,r2 视为 d d d)
现在暴力讨论 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3 的大小关系。
情况 1: x 1 > x 2 > x 3 x_1 > x_2 > x_3 x1>x2>x3
不难得出: w ( a , c ) + w ( b , d ) = x 1 + x 2 , w ( a , d ) + w ( b , c ) = x 2 + x 1 w(a, c) + w(b, d) =x_1 + x_2, w(a, d) + w(b, c) = x_2 + x_1 w(a,c)+w(b,d)=x1+x2,w(a,d)+w(b,c)=x2+x1,两者相等,满足四边形不等式。
情况 2: x 1 > x 3 > x 2 x_1 > x_3 > x_2 x1>x3>x2
不难得出: w ( a , c ) + w ( b , d ) = x 1 + x 3 , w ( a , d ) + w ( b , c ) = x 2 + x 1 w(a, c) + w(b, d) = x_1 + x_3, w(a, d) + w(b, c) = x_2 + x_1 w(a,c)+w(b,d)=x1+x3,w(a,d)+w(b,c)=x2+x1,显然满足 w ( a , c ) + w ( b , d ) > w ( a , d ) + w ( b , c ) w(a, c) + w(b, d) > w(a, d) + w(b, c) w(a,c)+w(b,d)>w(a,d)+w(b,c),满足四边形不等式。
情况 3: x 2 > x 1 > x 3 x_2 > x_1 > x_3 x2>x1>x3
不难得出: w ( a , c ) + w ( b , d ) = x 2 + x 2 , w ( a , d ) + w ( b , c ) = x 2 + x 2 w(a, c) + w(b, d) = x_2 + x_2, w(a, d) + w(b, c) = x_2 + x_2 w(a,c)+w(b,d)=x2+x2,w(a,d)+w(b,c)=x2+x2,两者相等,显然满足四边形不等式。
情况 4: x 1 < x 2 x_1 < x_2 x1<x2
不难证明这样选的话会让 d d d 对应 a a a 更优,所以这不符合我们的讨论。
综上, w ( a , c ) + w ( b , d ) ≥ w ( a , d ) + w ( b , c ) w(a, c) + w(b, d) \ge w(a, d) + w(b, c) w(a,c)+w(b,d)≥w(a,d)+w(b,c)。
Part.3/3 区间内相同值的对数
这里的 w ( l , r ) w(l, r) w(l,r) 指区间内所有数的相同值的对数。仍然考虑用定义证明。
任取四个位置 l 1 ≤ l 2 ≤ r 1 ≤ r 2 l_1 \le l_2 \le r_1 \le r_2 l1≤l2≤r1≤r2,我们要证明的就是 w ( l 1 , r 1 ) + w ( l 2 , r 2 ) ≤ w ( l 1 , r 2 ) + w ( l 2 , r 1 ) w(l_1, r_1) + w(l_2, r_2) \le w(l_1, r_2) + w(l_2, r_1) w(l1,r1)+w(l2,r2)≤w(l1,r2)+w(l2,r1)。
我们不失一般性地只讨论一种数出现的次数。
仍然像上面那样,设区间 [ l 1 , l 2 ) [l_1, l_2) [l1,l2) 中这种数的出现次数为 x 1 x_1 x1,区间 [ l 2 , r 1 ] [l_2, r_1] [l2,r1] 中的出现次数为 x 2 x_2 x2,区间 ( r 1 , r 2 ] (r_1, r_2] (r1,r2] 中的出现次数为 x 3 x_3 x3。
则可以得到:
w ( l 1 , r 1 ) + w ( l 2 , r 2 ) = ( x 1 + x 2 ) × ( x 1 + x 2 − 1 ) 2 + ( x 2 + x 3 ) × ( x 2 + x 3 − 1 ) 2 = x 1 2 + 2 x 1 x 2 + x 2 2 − x 1 − x 2 + x 2 2 + x 3 2 + 2 x 2 x 3 − x 2 − x 3 2 = x 1 2 + 2 x 2 2 + x 3 2 + 2 x 1 x 2 + 2 x 2 x 3 − x 1 − 2 x 2 − x 3 2 w ( l 1 , r 2 ) + w ( l 2 , r 2 ) = ( x 1 + x 2 + x 3 ) ( x 1 + x 2 + x 3 − 1 ) 2 + x 2 ( x 2 − 1 ) 2 = x 1 2 + x 2 2 + x 3 2 + 2 x 1 x 2 + 2 x 2 x 3 + 2 x 1 x 3 − x 1 − x 2 − x 3 + x 2 2 − x 2 2 = x 1 2 + 2 x 2 2 + x 3 2 + 2 x 1 x 2 + 2 x 2 x 3 + 2 x 1 x 3 − x 1 − 2 x 2 − x 3 2 \begin{aligned} w(l_1, r_1) + w(l_2, r_2) & = \frac{(x_1 + x_2) \times (x_1 + x_2 - 1)}{2} + \frac{(x_2 + x_3)\times(x_2 + x_3 - 1)}{2} \\ & = \frac{{x_1}^2 + 2x_1x_2 + {x_2}^2 - x_1 - x_2 + {x_2}^2 + {x_3}^2 + 2x_2x_3 - x_2 - x_3}{2} \\ & = \frac{{x_1}^2 + 2{x_2}^2 + {x_3}^2 + 2x_1x_2 + 2x_2x_3 - x_1 - 2x_2 - x_3}{2} \\ w(l_1, r_2) + w(l_2, r_2) & = \frac{(x_1 + x_2 + x_3)(x_1 + x_2 + x_3 - 1)}{2} + \frac{x_2(x_2 - 1)}{2} \\ & = \frac{{x_1}^2 + {x_2}^2 + {x_3}^2 + 2x_1x_2 + 2x_2x_3 + 2x_1x_3 - x_1 - x_2 - x_3 + {x_2}^2 - x_2}{2} \\ & = \frac{{x_1}^2 + 2{x_2}^2 + {x_3}^2 + 2x_1x_2 + 2x_2x_3 + 2x_1x_3 - x_1 - 2x_2 - x_3}{2} \end{aligned} w(l1,r1)+w(l2,r2)w(l1,r2)+w(l2,r2)=2(x1+x2)×(x1+x2−1)+2(x2+x3)×(x2+x3−1)=2x12+2x1x2+x22−x1−x2+x22+x32+2x2x3−x2−x3=2x12+2x22+x32+2x1x2+2x2x3−x1−2x2−x3=2(x1+x2+x3)(x1+x2+x3−1)+2x2(x2−1)=2x12+x22+x32+2x1x2+2x2x3+2x1x3−x1−x2−x3+x22−x2=2x12+2x22+x32+2x1x2+2x2x3+2x1x3−x1−2x2−x3
显然有 w ( l 1 , r 1 ) + w ( l 2 , r 2 ) ≤ w ( l 1 , r 2 ) + w ( l 2 , r 1 ) w(l_1, r_1) + w(l_2, r_2) \le w(l_1, r_2) + w(l_2, r_1) w(l1,r1)+w(l2,r2)≤w(l1,r2)+w(l2,r1)。
于是得到证明。
Part.4 例题
Part.4/1 UVa 10304 Optimal Binary Search Tree
Part.4/1-1 题目大意
将 N N N 个节点分成二叉搜索树,已知每个节点的权值是自小到大的。将第 i i i 个节点分到的深度为 d d d 时的代价为 d × c i d \times c_i d×ci(根节点的深度为 0 0 0),求最小代价总和。
Part.4/1-2 简析
定义状态 f ( i , j ) f(i, j) f(i,j) 为将区间 [ i , j ] [i, j] [i,j] 中的所有数分成一棵二叉搜索树的代价。不难列出最简单的状态转移方程:
f ( i , j ) = min k = i + 1 j − 1 { f ( i , k − 1 ) + f ( k + 1 , j ) + w ( i , j , k ) } f(i, j) = \min\limits_{k = i + 1}^{j - 1}\{f(i, k - 1) + f(k + 1, j) + w(i, j, k)\} f(i,j)=k=i+1minj−1{f(i,k−1)+f(k+1,j)+w(i,j,k)}
其中 w ( i , j , k ) w(i, j, k) w(i,j,k) 表示区间 [ i , j ] [i, j] [i,j] 以节点 k k k 为根时的代价。
若我们记 c i c_i ci 的前缀和为 s i s_i si,那么我们可以得到:
w ( i , j , k ) = s j − s i − 1 − c k w(i, j, k) = s_j - s_{i - 1} - c_k w(i,j,k)=sj−si−1−ck
显然这个 c k c_k ck 是在变化的,我们无法直接证明这个 w ( i , j , k ) w(i, j, k) w(i,j,k) 是满足四边形不等式和区间包含单调性的。
一个奇妙的想法就是直接将根节点的深度算成 1 1 1,这样一来状态转移方程就被改写成了:
f ( i , j ) = min k = i + 1 j − 1 { f ( i , k − 1 ) + f ( k + 1 , j ) } + s j − s i − 1 f(i, j) = \min\limits_{k = i + 1}^{j - 1} \{f(i, k - 1) + f(k + 1, j)\} + s_j - s_{i - 1} f(i,j)=k=i+1minj−1{f(i,k−1)+f(k+1,j)}+sj−si−1
最终答案就是 f ( 1 , n ) − s n f(1, n) - s_n f(1,n)−sn 了。
显然 s j − s i − 1 s_j - s_{i - 1} sj−si−1 满足区间包含单调性和四边形恒等式,所以直接用四边形不等式优化到 O ( N 2 ) O(N^2) O(N2)。
Part.4/2 AtCoder ARC067 D Yakiniku Restaurants
Part.4/2-1 题目大意
一条街上有 N N N 家烧烤店,从西到东编号为 1 1 1 至 N N N,第 i i i 家和 i + 1 i + 1 i+1 家之间的距离是 A i A_i Ai。
Joisino 有 M M M 张餐票,编号从 1 1 1 到 M M M。每家烧烤店都提供 M M M 种烧烤套餐,用不同编号的餐票可以换取不同种类的套餐。 在烧烤店 i i i,用编号为 j j j 的餐票可以买到美味值为 B i , j B_{i, j} Bi,j 的套餐。 每张餐票只能使用一次,但是在每个店可以使用任意数量的餐票。
Joisino 希望通过从她选择的一家店开始,然后反复前往另一家烧烤店并在该店使用还未使用的餐票来享用总共 M M M 个烧烤套餐。
她最终的幸福指数由以下公式计算得出:(所吃套餐的总美味度)-(经过的总路程)。
找到她最大可能的幸福指数。
Part.4/2-2 简析
不难贪心地想到我们选择的餐馆是连续的,且在中途是不会折返的,每张餐券都只会在获得的最大的美味值的餐馆中消耗掉。
记每个位置到第一家餐馆的距离为 x i x_i xi。
于是列出状态转移方程:
f ( l , r ) = ∑ j = 1 m max i = 1 n B i , j + x l − x r f(l, r) = \sum\limits_{j = 1}^{m}\max\limits_{i = 1}^{n}B_{i, j} + x_l - x_r f(l,r)=j=1∑mi=1maxnBi,j+xl−xr
如果我们打一下表可以发现,当 r r r 增大的时候, l l l 不会减小。
那么我们就不失一般性地考虑 j = 1 j = 1 j=1 的情况。
(其实这个部分和上面讲最大值的部分是一样的,就是多加了一个常数而已)
然后就可以用分治来乱搞了。
Part.4/3 SPOJ ADAMOLD Ada and Mold
Part.4/3-1 题目大意
给定一个数列 A i A_i Ai。将从区间 [ l , r ] [l, r] [l,r] 的数划分成一段的代价为区间中的数两两异或的和。将这个序列划分为 K + 1 K + 1 K+1 段,求最小的划分代价。
Part.4/3-2 简析
不难证明这个 w ( l , r ) w(l, r) w(l,r) 是满足四边形不等式的,至于具体怎么证的就留给读者们自己练习一下吧。(相信你一定能够自己证出来的)
要把这个按照二进制位拆开来用推论证明。仍然是暴力讨论区间的 0 0 0 和 1 1 1 的个数。
Part.5 参考实现
UVa 10304 Optimal Binary Search Tree
#include AtCoder ARC067 D Yakiniku Restaurants
#include SPOJ ADAMOLD Ada and Mold
分治
#include 枚举
#include 参考资料
- OI-WIKI
- Lucky_Glass 的博客
- ybwowen 的博客
后记
MD 这 10000 多字的博客快要把我的 XP 搞炸了 QAQ。。。(似乎奔腾 E5700 + 2GB 内存也。。。)