Chomp游戏

Chomp游戏

Bat特白

人生不只有眼前的狗，且还有远方的狮

14 人赞了该文章

（题图致敬PAC-MAN）

Chomp是一个双人游戏，有  块曲奇饼排成一个矩形格状，称作棋盘。两个玩家轮流自选吃掉一块还剩下的曲奇饼，而且要把它右边和下面所有的曲奇饼都被取走（如果存在）。如果不吃左上角的那一块曲奇饼（位置记为(1, 1)）就没有其他选择的玩家为失败。

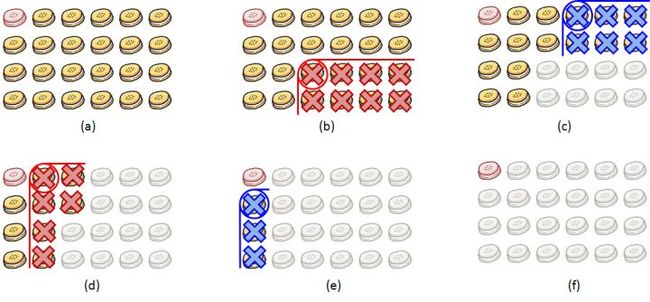
下图展示了一个棋盘为  的Chomp游戏的完整过程：

• (a)是初始情况；
• (b)表示玩家一吃掉位置为(3, 3)的曲奇饼；
• (c)表示玩家二吃掉位置为(1, 4)的曲奇饼；
• (d)表示玩家一吃掉位置为(1, 2)的曲奇饼；
• (e)表示玩家二吃掉位置为(2, 1)的曲奇饼；
• (f)表示玩家一在游戏中落败。

（我很好奇明明清清楚楚的图，上传了怎么就这么模糊(╯' - ')╯︵ ┻━┻ ）

---

分析这个游戏的“策略”之前先“插播”一个重要结果——

1913年，恩斯特·策梅洛（Ernst Zermelo）在论文《Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels》中证明了策梅洛定理（Zermelo's theorem），定理表明在二人参与的游戏中，如果满足

• 游戏步骤有限；
• 信息完备（可以理解为参与者知道所有与游戏相关的信息以及本次游戏中已发生所有步骤和结果）；
• 不会产生平局；
• 确定性的（即运气因素并不牵涉在游戏中），

则或者先行一方有必胜策略，或者后行一方有必胜策略。

 

策梅洛定理的另一种表述是：在二人参与的游戏中，如果满足游戏步骤有限、信息完备、每一步骤都是确定性，则或者先行一方有必胜策略，或者先行一方有必和策略，或者后行一方有必胜策略。

---

下面证明：除去  大小的棋盘外，其他大小的棋盘，先手存在必胜策略。

证明：

假设棋盘规模为  。

首先，游戏不可能产生平局。

其次，由于每一步移动至少吃掉1块曲奇饼干，因此不超过  步后游戏必定结束。

由策梅洛定理，这个确定性二人有限游戏信息完备，且不存在平局，则或者先行一方有必胜策略，或者后行一方有必胜策略。

如果后手有必胜策略，使得无论先手第一次取哪个石子，后手都能获得最后的胜利。

那么现在假设先手取最右下角的石子  ，接下来后手可以取某块曲奇  使得自己进入必胜的局面。

事实上，先手在第一次取的时候就可以取曲奇  ，之后完全模仿后手的必胜步骤，迫使后手失败。

于是产生矛盾。因此不存在后手必胜策略，先手存在必胜策略。

 

注意：这个证明是非构造性存在性证明，也即只是证明了先手必胜策略的存在性，但没有构造出具体必胜策略。

虽然对于一些特殊的情况，比如棋盘是正方形、棋盘只有两行，可以找到必胜策略；但对于一般情况，还没有人能具体给出Chomp的一般性必胜策略。

---

(Ⅰ) 棋盘只有一行，但是多于一格。先手只要只剩下左上角的一块即可。

(Ⅱ) 棋盘是正方形，但是多于一格。先手只要只剩下左上角的一块、最上一行、最左一列即可。

之后，无论后手怎么做，先手只要对称地模仿就可以。

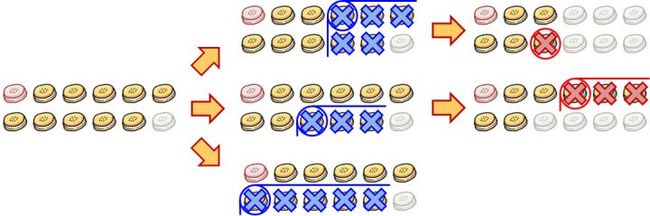
(Ⅲ) 棋盘只有两行，就先拿去右下角的一块。

之后 根据后手的选择，主要有三种可能，总体来说就是保持上行比下行曲奇饼多一，或者干脆对方取走下面一行全部曲奇饼。（其实下图中后两种可以合并）

---

Chomp游戏的变形：

(a) 三维Chomp游戏。将曲奇排成  的立方体，两个玩家轮流自选吃掉一块剩下的曲奇饼，若取走的曲奇饼为  ，则也要取走所有满足  ，  ，  的曲奇饼（如果存在）。

可以类似地将Chomp游戏扩展到任意维，并可以类似地证明，先手都存在必胜策略。

(b) 约数游戏。给定一个大于1的自然数  ，两个游戏参与者轮流选择N的大于1的正约数，但不可选择之前被选择过的因子的倍数（例如  ，有一方之前选择了4，则之后任一方都不可以再选择36）。

(c) 删数游戏：给定整数集合  ，两个人轮流从中选择一个数字，并将它和它的约数从集合中删除，删除最后一个数的人获胜。

类似Chomp游戏，得到结论就是无论  是几，都是先手必胜。

(d) 有限偏序集上的Chomp游戏。

Chomp游戏可以推广到在任意一个存在最小元  的有限偏序集  上：两名游戏者轮流选择S中的元素  ，移走  以及所有  中比  大的元素。失败者是被迫选择最小元  的玩家。

如果  有最大元素  ，那么在偏序集上的Chomp游戏存在一个获胜策略。

而且

1. 传统Chomp游戏与偏序集  上的Chomp游戏相同，其中  是  的所有正因子组成的集合，这里  和  是两个不同的素数。
2. 假设  和  都是全序集，证明：传统Chomp游戏与积偏序集  上的Chomp游戏相同。