Andres_Lionel
Andres_Lionel

树数数【智算之道复赛E】【树链剖分+dfs序】

题目链接

树数数【智算之道复赛E】【树链剖分+dfs序】_第1张图片

  我们可以考虑一个黑点u，它作为LBCA点所产生贡献次数为cnt[u] = \frac{size[u] * (size[u] - 1)}{2} - \sum cnt[son[u]]，其中，son[u]指的是u的子孙节点们，那么，u点作为LBCA点的贡献值就可以求出来了，就是cnt[u] * w[u]了。

  根据这样的关系，我们可以推导改变所带来的信息变化。

  • 白点变黑点

  那么，它的影响只会对它向上最近的黑色节点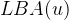LBA(u)产生直接影响，对于再往上的黑色节点，由于被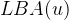LBA(u)给阻断了，所以受不到影响，同时，它会产生贡献，它产生的贡献就可以通过cnt[u] = \frac{size[u] * (size[u] - 1)}{2} - \sum cnt[son[u]]来计算得到。

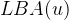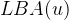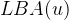  对于LBA(u)节点的影响呢？那么，其实相当于LBA(u)节点就会少去了cnt[u]这些部分了，所以它要减去cnt[u]的部分，似乎这样就达成了一个能量守恒，一个加cnt[u]，一个减去cnt[u]，所以确确实实对LBA(u)之上的黑点就没有影响了。

  • 黑点变白点

  我们看到白点变黑点时候的变化，那么黑点变白点可以考虑成“白点变黑点的逆变换”。

  于是，我们先对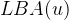LBA(u)加上cnt[u]的贡献，然后再是对u节点减去它的这些贡献次数，因为它要变成白点了呀。

  所以，这个问题全程围绕着cnt[u] = \frac{size[u] * (size[u] - 1)}{2} - \sum cnt[son[u]]这个关键的等式展开，求解了这些问题。

  然后关于怎么去找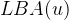LBA(u)点，这个可以用树剖去找dfs序最大的点，那么就一定同时满足深度最深的黑点（dfs序和深度关系），也就是距离u最近的黑点了。

  剩下的一些，几乎都是单点修改和区间更新的问题了，可以使用dfs序维护出来的线段树来解决该问题。

给几组测试数据：

/*
4 4
1 2 3
1 2 5 5
Q 2
F 3
M 3 11451
Q 2
*/
/*
5 4
1 1 2 2
3 1 2 4 2
F 1
M 1 2
F 4
Q 2
ans:
6
*/
/*
6 4
1 1 2 2 3
6 5 4 3 2 1
F 2
F 3
F 1
Q 1
ans:
85
*/

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 2e5 + 7;
int N, Q;
ll w[maxN];
namespace Graph
{
    int head[maxN], cnt;
    struct Eddge
    {
        int nex, to;
        Eddge(int a=-1, int b=0):nex(a), to(b) {}
    } edge[maxN];
    inline void addEddge(int u, int v)
    {
        edge[cnt] = Eddge(head[u], v);
        head[u] = cnt++;
    }
    inline void init()
    {
        cnt = 0;
        for(int i=1; i<=N; i++) head[i] = -1;
    }
};
using namespace Graph;
namespace Tree_Divide
{
    int deep[maxN], fa[maxN], siz[maxN], wson[maxN];
    void dfs_1(int u)
    {
        siz[u] = 1; wson[u] = 0;
        for(int i=head[u], v; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            deep[v] = deep[u] + 1;
            dfs_1(v);
            siz[u] += siz[v];
            if(siz[v] > siz[wson[u]]) wson[u] = v;
        }
    }
    int top[maxN], tot, dfn[maxN], end_tim[maxN], rid[maxN] = {0};
    void dfs_2(int u, int topy)
    {
        dfn[u] = ++tot;
        rid[tot] = u;
        top[u] = topy;
        if(wson[u]) dfs_2(wson[u], topy);
        for(int i=head[u], v; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            if(v == wson[u]) continue;
            dfs_2(v, v);
        }
        end_tim[u] = tot;
    }
    int t[maxN << 2] = {0};
    void Change(int rt, int l, int r, int qx)
    {
        if(l == r) { t[rt] ^= l; return; }
        int mid = HalF;
        if(qx <= mid) Change(Lson, qx);
        else Change(Rson, qx);
        t[rt] = max(t[lsn], t[rsn]);
    }
    int Find(int rt, int l, int r, int ql, int qr)
    {
        if(ql <= l && qr >= r) return t[rt];
        int mid = HalF;
        if(qr <= mid) return Find(QL);
        else if(ql > mid) return Find(QR);
        else return max(Find(QL), Find(QR));
    }
    inline int _LBA(int u)
    {
        if(!u) return 0;
        int ans = 0;
        while(top[u] ^ 1)
        {
            ans = Find(1, 1, N, dfn[top[u]], dfn[u]);
            if(ans) break;
            u = fa[top[u]];
        }
        if(!ans) ans = Find(1, 1, N, dfn[1], dfn[u]);
        return rid[ans];
    }
};
using namespace Tree_Divide;
namespace Segement
{
    ll sum[maxN << 2], ans[maxN << 2];
    void update(ll *tree, int rt, int l, int r, int qx, ll val)
    {
        if(l == r) { tree[rt] = val; return; }
        int mid = HalF;
        if(qx <= mid) update(tree, Lson, qx, val);
        else update(tree, Rson, qx, val);
        tree[rt] = tree[lsn] + tree[rsn];
    }
    ll query(ll *tree, int rt, int l, int r, int ql, int qr)
    {
        if(ql <= l && qr >= r) return tree[rt];
        int mid = HalF;
        if(qr <= mid) return query(tree, QL);
        else if(ql > mid) return query(tree, QR);
        else return query(tree, QL) + query(tree, QR);
    }
};
using namespace Segement;
bool col[maxN] = {false};
int main()
{
    scanf("%d%d", &N, &Q);
    init();
    for(int i=2; i<=N; i++)
    {
        scanf("%d", &fa[i]);
        addEddge(fa[i], i);
    }
    for(int i=1; i<=N; i++) scanf("%lld", &w[i]);
    deep[1] = 1;
    dfs_1(1);
    dfs_2(1, 1);
    char op[3];
    ll tmp, det, flba, nw, old_sum, new_sum;
    for(int i=1, u; i<=Q; i++)
    {
        scanf("%s%d", op, &u);
        switch (op[0])
        {
            case 'Q':
            {
                tmp = query(ans, 1, 1, N, dfn[u], end_tim[u]);
                if(!col[u])
                {
                    flba = _LBA(u);
                    if(flba)
                    {
                        old_sum = 1LL * siz[u] * (siz[u] - 1) / 2LL - query(sum, 1, 1, N, dfn[u], end_tim[u]);
                        tmp += old_sum * w[flba];
                    }
                }
                printf("%lld\n", tmp);
                break;
            }
            case 'M':
            {
                scanf("%lld", &nw);
                if(col[u])
                {
                    tmp = query(sum, 1, 1, N, dfn[u], dfn[u]);
                    update(ans, 1, 1, N, dfn[u], nw * tmp);
                }
                w[u] = nw;
                break;
            }
            default:
            {
                flba = _LBA(fa[u]);
                det = 1LL * siz[u] * (siz[u] - 1) / 2LL;
                if(siz[u] > 1) det -= query(sum, 1, 1, N, dfn[u] + 1, end_tim[u]);
                if(col[u])
                {
                    if(flba)
                    {
                        old_sum = query(sum, 1, 1, N, dfn[flba], dfn[flba]);
                        new_sum = old_sum + det;
                        update(sum, 1, 1, N, dfn[flba], new_sum);
                        update(ans, 1, 1, N, dfn[flba], new_sum * w[flba]);
                    }
                    update(sum, 1, 1, N, dfn[u], 0);
                    update(ans, 1, 1, N, dfn[u], 0);
                }
                else
                {
                    update(sum, 1, 1, N, dfn[u], det);
                    update(ans, 1, 1, N, dfn[u], det * w[u]);
                    if(flba)
                    {
                        old_sum = query(sum, 1, 1, N, dfn[flba], dfn[flba]);
                        new_sum = old_sum - det;
                        update(sum, 1, 1, N, dfn[flba], new_sum);
                        update(ans, 1, 1, N, dfn[flba], new_sum * w[flba]);
                    }
                }
                col[u] ^= 1;
                Change(1, 1, N, dfn[u]);
                break;
            }
        }
    }
    return 0;
}

 

你可能感兴趣的:(树链剖分,线段树,树链剖分,dfs序,线段树)

  • BZOJ 五月胡乱补题 nike0good 其他屯题bzoj博客补档
    旧博客搬运部分格式还没来得及改T_T【BZOJ4806:炮】同BZOJ1801【BZOJ3242:[Noi2013]快餐店】树形dp，要么最远点在同一颗树上（dp），要么在不同树上，此时答案=去掉任何一条边后形成的树的答案的最小值，我们枚举去掉的那条边。由于答案=s[i]-s[j]+dis[i]+dis[j]，i，j可以分开考虑，也可以用线段树解决。【BZOJ4878:[Lydsy2017年5月月
  • 线段树（模板） 数学收藏家 线段树
    #includeusingnamespacestd;#defineintlonglong#defineendl'\n'#defineIOSios::sync_with_stdio(false);cin.tie(0);cout.tie(0);#definemaxn100005intn,q;inta[maxn];structnode{intval,lazy;}s[maxn*4];voidpush_up
  • CCF-CSP认证考试（第32次）总结+题解 Romanticroom 算法
    总结：这一次我选了时间较近的一次进行练习，结果有点悲，前两题就一个质因数分解还好，第三题我走了弯路，想通过类似线段树的手段处理，结果还差了系数，最后一个点tle了。。。第四题直接放弃了。。（太菜，没脸见人）第五题还抱有幻想，当然也只有幻想。。后两题只能打暴力了，以我现在水平，希望努力一个月能有所改变吧。题解：（这里只给到三题题解，再往后我也不会了。。）题一：仓库规划西西艾弗岛上共有n个仓库，依次编
  • 【图论】虚树 - 模板总结 Texcavator 图论图论
    适用于解决一棵树中只需要用到少部分点的时候，将需要用到的点提出来单独建一棵树/*********************虚树*********************/structedge{intto,next;intval;};structVirtual_Tree{intn;//点数intdfn[N];//dfs序intdep[N];//深度intfa[N][25],m[N];intnum;//
  • 数据结构入门（5）——树与二叉树的应用 Dusk Cteator 高级语言程序设计数据结构笔记数据结构算法霍夫曼树二叉树c++
    数据结构入门——树与二叉树的应用文章目录数据结构入门——树与二叉树的应用前言一、压缩与哈夫曼树扩充二叉树哈夫曼算法哈夫曼算法基本思想哈夫曼算法哈夫曼编码二、表达式树如何构造表达式二叉树计算表达式二叉树对应的值三、并查集并查集的实现四、初探线段树与树状数组线段树线段树操作树状数组定义操作树状数组和线段树前言本系列文章将简要介绍数据结构课程入门知识，文章将结合我们学校（吉大）数据结构课程内容进行讲述。
  • 线段树 Cheng Yu 线段树线段树
    基础知识1、线段树是二叉树，且必定是平衡二叉树，但不一定是完全二叉树。2、对于区间[L,R]，令mid=(L+R)/2，则其左子树为[L,mid]，右子树为[mid+1,R]，当L==R时，该区间为线段树的叶子，无需继续往下划分。3、线段树虽然不是完全二叉树，但是可以用完全二叉树的方式去构造并存储它，只是最后一层可能存在某些叶子与叶子之间出现“空叶子”，这个无需理会，同样给空叶子按顺序编号，在遍历
  • 【详解】线段树 CH_Vaniteux 详解数据结构线段树
    线段树详解By岩之痕目录：一：综述二：原理三：递归实现四：非递归原理五：非递归实现六：线段树解题模型七：扫描线八：可持久化(主席树)九：练习题一：综述假设有编号从1到n的n个点，每个点都存了一些信息，用[L,R]表示下标从L到R的这些点。线段树的用处就是，对编号连续的一些点进行修改或者统计操作，修改和统计的复杂度都是O(log2(n)).线段树的原理，就是，将[1,n]分解成若干特定的子区间(数量
  • P1656 炸铁路（割边模板） OMG_NOIP 算法数据结构省选复习c++算法
    ~~~~~原题链接~~~~~总题单链接割边的定义~~~~~若在一张无向图中，删除一条边后连通块的数量会增加，则这条边是割边。怎么找割边~~~~~按dfs序dfs序dfs序访问图上的每个点，每个点只访问一遍。~~~~~对于图上的每个点，记录dfn[i]dfn[i]dfn[i]表示点iii第一次被访问到的时间戳，low[i]low[i]low[i]表示点iii不走进入点iii的反边的情况下能走到的最早
  • CF 967 D. Longest Max Min Subsequence Jiu-yuan 算法数据结构
    原题链接：Problem-D-Codeforces题意：多测，每次给出长度为n的数组，要求找出没有重复元素的，最长的子序列，如果不止一个最长子序列，那么就选择字典序最小的，比较字典序的时候，如果这个元素的下标是奇数，那么就变成负数比较。思路：线段树+贪心，观察题意可知，最终的子序列肯定是正负相间的，那么对于奇数位置，这个数越大越好，对于偶数位置，这个数越小越好。那么就可以贪心的考虑这个问题，设置二
  • E. Linear Kingdom Races Lanthanmum 算法数据结构动态规划
    https://codeforces.com/problemset/problem/115/E线段树优化dpO(n2)->O(nlogn)分析题意发现可以有暴力dpdp(i)是前i条路最大利润dp(i)=dp(i-1)不选第i条路dp(i)=max(dp(j)+val(j)-cost(j))选这i条路dp(i)=max(dp(i-1),max(dp(j)+val(j)-cost(j))显然右边值可
  • c语言专属英语单词,C语言 V 编程英语单词.doc 时间还早 c语言专属英语单词
    编程词汇英汉对照DataStructures基本数据结构Dictionaries字典PriorityQueues堆GraphDataStructures图SetDataStructures集合Kd-Trees线段树NumericalProblems数值问题SolvingLinearEquations线性方程组BandwidthReduction带宽压缩MatrixMultiplication矩阵乘
  • 牛客竞赛数据结构专题班树状数组、线段树练习题 Landing_on_Mars #线段树数据结构算法
    牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJG智乃酱的平方数列（线段树，等差数列，多项式）题目描述想必你一定会用线段树维护等差数列吧？让我们来看看它的升级版。请你维护一个长度为5×10^5的数组，一开始数组中每个元素都为0，要求支持以下两个操作：1、区间[l,r]加自然数的平方数组，即al+=1，al+1+=4，al+2+=9，al+3+=16...ar+
  • 主席树求区间第K小模板 Stephen_Curry___ 算法c++数据结构主席树
    主席树（PresidentTree）是一种用于解决区间查询和修改问题的数据结构，通常用于静态区间问题（即查询和修改操作在构建结构之后不再发生变化）。主席树可以高效地处理诸如区间和、区间最值等问题。主席树的实现原理：基本思想：主席树是一种基于分治思想的数据结构，它将原始序列按照每个位置的取值范围进行离散化，然后构建出一棵持久化线段树（PersistentSegmentTree）。持久化线段树：持久化
  • 【算法随笔：HDU 3333 Turing tree】(线段树 | 离线 | 离散化 | 贪心） XNB's Not a Beginner 算法算法哈希算法leetcodec++排序算法
    https://acm.hdu.edu.cn/showproblem.php?pid=3333https://acm.hdu.edu.cn/showproblem.php?pid=3333https://vjudge.net.cn/problem/HDU-3333https://vjudge.net.cn/problem/HDU-3333题目很简单，给出长度为N的数组，Q次询问，每次给出区间[x,
  • 【数据结构题目讲解】BZOJ 3306 - 树 利用DFS序求解 阿史大杯茶 数据结构经典数据结构算法c++
    BZOJ3306-树Description\mathrm{Description}Description给定111棵以111为根节点的nnn个点的树，接下来有mmm次操作：Vxy将xxx点的权值更改为yyyEx将根改为xxx点Qx查询xxx子树的最小值Solution\mathrm{Solution}Solution首先，考虑如果没有换根操作（即E操作），那么直接使用DFS序配合线段树的方式即可解
  • Splay 荼白777 平衡树算法数据结构
    定义Splay是一颗平衡二叉树，但是往往没那么平衡，期望高度是log(n)log(n)log(n)应用不仅支持普通平衡树的操作，包括一些区间问题(一般用线段树解决)的也支持；保证高度的思想对某个结点进行操作的时候，将其旋转到树根；这里的操作指的是像插入，查询等等；也就是说，这跟操作系统的局部性原理类似，某个点既然当前用到了，那么后续肯定还会用到；拉到根结点其实就是进行了一个类似缓存的操作；应用这个
  • 蓝桥杯：C++二叉树 DaveVV 蓝桥杯c++蓝桥杯c++算法数据结构c语言
    二叉树几乎每次蓝桥杯软件类大赛都会考核二叉树，它或者作为数据结构题出现，或者应用在其他算法中。大部分高级数据结构是基于二叉树的，例如常用的高级数据结构线段树就是基于二叉树的。二叉树应用广泛和它的形态有关。二叉树的定义：二叉树的第1层是一个结点，称为根，它最多有两个子结点，分别是左子结点、右子结点，以它们为根的子树称为左子树、右子树。二叉树上的每个结点，都是按照这个规则逐层往下构建出来的。图3.4二
  • 动态DP入门&线性动态DP 罗博士 ACM动态规划动态规划算法ACM
    动态DP入门&线性动态DP前言核心思想例1例22024牛客寒假4K2022牛客寒假2J结论前言OI-WiKi上有一个动态DP讲解，直接讲到了树型DP领域，同时需要树链剖分，门槛有点高。本文针对线性DP做一个动态DP的讲解。首先当然要懂得一定的DP的相关知识，然后需要知道DP方程的矩阵表达。可以看这里——根据递推公式构造系数矩阵用于快速幂。很多DP的状态转移方程都可以写成矩阵形式，由此就有了矩阵快速
  • 【算法】树状数组和线段树 柳下敲代码 算法算法数据结构c++
    文章目录一、树状数组二、线段树一、树状数组O(logn)O(logn)O(logn)：单点修改、区间查询与前缀和的区别：前缀和是离线的，每次动态修改原数组某个元素，都需要重新求一遍前缀和，因此单点修改是O(n)O(n)O(n)的，区间查询则是O(1)O(1)O(1)树状数组是在线的，单点修改和区间查询都是O(logn)O(logn)O(logn)设下标从111开始//树状数组的定义t[x]=a[x
  • 【图论经典题目讲解】CF786B - Legacy 一道线段树优化建图的经典题目 阿史大杯茶 图论经典图论c++算法
    CF786B−Legacy\mathrm{CF786B-Legacy}CF786B−LegacyDescription\mathrm{Description}Description给定111张nnn个点的有向图，初始没有边，接下来有qqq次操作，形式如下：1uvw表示从uuu向vvv连接111条长度为www的有向边2ulrw表示从uuu向iii（i∈[l,r]i\in[l,r]i∈[l,r]）连接
  • 最小DFS序 coduck_lys 深度优先图论算法
    时间限制：1秒内存限制：128M题目描述一般来讲，我们在对树进行深度优先遍历时，对于每个节点，在刚进入递归后以及即将回溯前各记录一次该节点的编号，最后产生一个长度为2n的节点的序列就称为树的DFS序。输入描述第一行，两个整数n(1usingnamespacestd;constintN=2005;inthead[N],vis[N],ver[N],Next[N],tot=-1,n,S;structno
  • 算法分类合集 weixin_30784945
    算法分类合集ACM所有算法数据结构栈，队列，链表哈希表，哈希数组堆，优先队列双端队列可并堆左偏堆二叉查找树Treap伸展树并查集集合计数问题二分图的识别平衡二叉树二叉排序树线段树一维线段树二维线段树树状数组一维树状数组N维树状数组字典树后缀数组，后缀树块状链表哈夫曼树桶，跳跃表Trie树(静态建树、动态建树)AC自动机LCA和RMQ问题KMP算法图论基本图算法图广度优先遍历深度优先遍历拓扑排序割边
  • ACM算法分类（要学习的东西还很多） 还是太年轻
    ACM所有算法数据结构栈，队列，链表哈希表，哈希数组堆，优先队列双端队列可并堆左偏堆二叉查找树Treap伸展树并查集集合计数问题二分图的识别平衡二叉树二叉排序树线段树一维线段树二维线段树树状数组一维树状数组N维树状数组字典树后缀数组，后缀树块状链表哈夫曼树桶，跳跃表Trie树(静态建树、动态建树)AC自动机LCA和RMQ问题KMP算法图论基本图算法图广度优先遍历深度优先遍历拓扑排序割边割点强连通分
  • ACM算法目录 龍木
    ACM所有算法数据结构栈，队列，链表哈希表，哈希数组堆，优先队列双端队列可并堆左偏堆二叉查找树Treap伸展树并查集集合计数问题二分图的识别平衡二叉树二叉排序树线段树一维线段树二维线段树树状数组一维树状数组N维树状数组字典树后缀数组，后缀树块状链表哈夫曼树桶，跳跃表Trie树(静态建树、动态建树)AC自动机LCA和RMQ问题KMP算法图论基本图算法图广度优先遍历深度优先遍历拓扑排序割边割点强连通分
  • 看歌词猜歌 线段树 myjs999 链表
    voidmodify(node*tempnode,inttempleft,inttempright){if(templeft==tempright){//目标点（叶子结点）tempnode->maxnum=aimnum;return;}intmiddle=(templeft+tempright)/2;if(aimpleftchild,templeft,middle);elsemodify(temp
  • 异或和 蓝桥杯2024python省赛 题解 鱼香猫猫头 蓝桥杯pythonjavac++算法数据结构
    异或和题意经典的树上单点修改+子树求和的问题。那么我们首先可以想到构建出树的dfs序，将原本一棵树上的内容转化为一个数组。再由于异或运算和加法一样具有可逆性，所以使用树状数组维护即可。然后由于树状数组维护的性质有限，每次只能额外异或一个数而不能直接进行赋值，所以我们保留好原数组，每次给单点赋值时，视为异或上“原来的值异或现在的值”就可以了。复杂度为O(mlogn)。附上python代码import
  • 2021-07-20 RX-0493
    1.MyCowAteMyHomeworkS：坑点：计算小数时，除数一定要强制转化为double型，(ans=sum/(double)(n-i))，ans为double，sum可以为int2.MooFestG：学习了cdq分治，将其中一维从n的枚举，压缩到logn的枚举，枚举区间。[1,1]->[1,2]->[1,4],以此类推3.XOR的艺术：线段树，pushdown还有Add可以实现区间；数组开
  • 基于完全二叉树实现线段树-- [爆竹声中一岁除,线段树下苦踌躇] 摆烂小青菜 图论数据结构算法笔记数据结构深度优先算法
    文章目录一.完全二叉树完全二叉树的父子结点引索关系二.线段树三.基于完全二叉树实现线段树关于线段树的结点数量问题的证明递归建树递归查询区间和递归单点修改线段树模板题一.完全二叉树完全二叉树的物理结构是线性表,逻辑结构是二叉树完全二叉树的父子结点引索关系通过子结点下标引索父结点下标:父结点下标=子节点下标/2;通过父结点下标引索左孩子下标:左孩子下标=父结点下标*2;通过父结点下标引索右孩子下标:右
  • 线段树简单笔记 明月千里赴迢遥 数据结构ACM蓝桥杯
    一经典线段树结构：权值为[L,R]的区间和intL,R,sum;操作1单点修改O（logn）递归找到相应叶子节点，回溯时修改父节点（两个儿子总和）操作2区间查询O(logn)左右两边递归，递归边界为左右两边都被包含，累加其权值最坏耗时4logn区间修改需要懒标记，蓝桥杯一般考不到，即使考到也是特殊区间修改，用不到函数1pushup用子节点信息更新当前节点信息2build在一段区间上初始化线段树3m
  • 数据结构总结 broxin 学习日志
    一、树链刨分按照重儿子分就行了，理论复杂度是log^2的，但事实上常数比较小。我YY了一个优化的方法：如果题目只涉及路径的修改，可以针对每个重链单独建一棵线段树（这样必须用指针表示儿子），然后可以发现除了u,v,lca(u,v)三个点需要深入线段树中，其他的重链在线段树的根节点读了值就直接返回了，这样写复杂度是logn的，操作量特别大的题可以看出明显的差距。但是如果题目同时涉及路径和子树的修改（N
  • 二分查找排序算法 周凡杨 java二分查找排序算法折半
    一：概念 二分查找又称 折半查找（ 折半搜索/ 二分搜索），优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而 查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表 分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步
  • java中的BigDecimal bijian1013 javaBigDecimal
            在项目开发过程中出现精度丢失问题，查资料用BigDecimal解决，并发现如下这篇BigDecimal的解决问题的思路和方法很值得学习，特转载。         原文地址：http://blog.csdn.net/ugg/article/de
  • Shell echo命令详解 daizj echoshell
    Shell echo命令 Shell 的 echo 指令与 PHP 的 echo 指令类似，都是用于字符串的输出。命令格式： echo string 您可以使用echo实现更复杂的输出格式控制。 1.显示普通字符串: echo "It is a test" 这里的双引号完全可以省略，以下命令与上面实例效果一致： echo Itis a test 2.显示转义
  • Oracle DBA 简单操作 周凡杨 oracle dba sql
    --执行次数多的SQL select sql_text,executions from (      select sql_text,executions from v$sqlarea order by executions desc      ) where rownum<81;  &nb
  • 画图重绘 朱辉辉33 游戏
      我第一次接触重绘是编写五子棋小游戏的时候，因为游戏里的棋盘是用线绘制的，而这些东西并不在系统自带的重绘里，所以在移动窗体时，棋盘并不会重绘出来。所以我们要重写系统的重绘方法。   在重写系统重绘方法时，我们要注意一定要调用父类的重绘方法，即加上super.paint(g)，因为如果不调用父类的重绘方式，重写后会把父类的重绘覆盖掉，而父类的重绘方法是绘制画布，这样就导致我们
  • 线程之初体验 西蜀石兰 线程
    一直觉得多线程是学Java的一个分水岭，懂多线程才算入门。 之前看《编程思想》的多线程章节，看的云里雾里，知道线程类有哪几个方法，却依旧不知道线程到底是什么？书上都写线程是进程的模块，共享线程的资源，可是这跟多线程编程有毛线的关系，呜呜。。。 线程其实也是用户自定义的任务，不要过多的强调线程的属性，而忽略了线程最基本的属性。 你可以在线程类的run()方法中定义自己的任务，就跟正常的Ja
  • linux集群互相免登陆配置 林鹤霄 linux
    配置ssh免登陆 1、生成秘钥和公钥    ssh-keygen -t rsa 2、提示让你输入，什么都不输，三次回车之后会在~下面的.ssh文件夹中多出两个文件id_rsa 和 id_rsa.pub    其中id_rsa为秘钥，id_rsa.pub为公钥，使用公钥加密的数据只有私钥才能对这些数据解密    c
  • mysql : Lock wait timeout exceeded; try restarting transaction aigo mysql
    原文：http://www.cnblogs.com/freeliver54/archive/2010/09/30/1839042.html   原因是你使用的InnoDB   表类型的时候, 默认参数:innodb_lock_wait_timeout设置锁等待的时间是50s, 因为有的锁等待超过了这个时间,所以抱错.   你可以把这个时间加长,或者优化存储
  • Socket编程 基本的聊天实现。 alleni123 socket
    public class Server { //用来存储所有连接上来的客户 private List<ServerThread> clients; public static void main(String[] args) { Server s = new Server(); s.startServer(9988); } publi
  • 多线程监听器事件模式(一个简单的例子) 百合不是茶 线程监听模式
        多线程的事件监听器模式   监听器时间模式经常与多线程使用,在多线程中如何知道我的线程正在执行那什么内容,可以通过时间监听器模式得到        创建多线程的事件监听器模式 思路:    1, 创建线程并启动,在创建线程的位置设置一个标记     2,创建队
  • spring InitializingBean接口 bijian1013 javaspring
    spring的事务的TransactionTemplate，其源码如下： public class TransactionTemplate extends DefaultTransactionDefinition implements TransactionOperations, InitializingBean{ ... } TransactionTemplate继承了DefaultT
  • Oracle中询表的权限被授予给了哪些用户 bijian1013 oracle数据库权限
            Oracle查询表将权限赋给了哪些用户的SQL，以备查用。 select t.table_name as "表名", t.grantee as "被授权的属组", t.owner as "对象所在的属组"
  • 【Struts2五】Struts2 参数传值 bit1129 struts2
    Struts2中参数传值的3种情况 1.请求参数绑定到Action的实例字段上 2.Action将值传递到转发的视图上 3.Action将值传递到重定向的视图上   一、请求参数绑定到Action的实例字段上以及Action将值传递到转发的视图上 Struts可以自动将请求URL中的请求参数或者表单提交的参数绑定到Action定义的实例字段上，绑定的规则使用ognl表达式语言
  • 【Kafka十四】关于auto.offset.reset[Q/A] bit1129 kafka
    I got serveral questions about  auto.offset.reset. This configuration parameter governs how  consumer read the message from  Kafka when  there is no initial offset in ZooKeeper or
  • nginx gzip压缩配置 ronin47 nginx gzip 压缩范例
    nginx gzip压缩配置 更多 0 nginx gzip 配置   随着nginx的发展，越来越多的网站使用nginx，因此nginx的优化变得越来越重要，今天我们来看看nginx的gzip压缩到底是怎么压缩的呢？ gzip(GNU-ZIP)是一种压缩技术。经过gzip压缩后页面大小可以变为原来的30%甚至更小，这样，用
  • java-13.输入一个单向链表，输出该链表中倒数第 k 个节点 bylijinnan java
    two cursors. Make the first cursor go K steps first. /* * 第 13 题：题目：输入一个单向链表，输出该链表中倒数第 k 个节点 */ public void displayKthItemsBackWard(ListNode head,int k){ ListNode p1=head,p2=head;
  • Spring源码学习-JdbcTemplate queryForObject bylijinnan javaspring
    JdbcTemplate中有两个可能会混淆的queryForObject方法： 1. Object queryForObject(String sql, Object[] args, Class requiredType) 2. Object queryForObject(String sql, Object[] args, RowMapper rowMapper) 第1个方法是只查
  • [冰川时代]在冰川时代,我们需要什么样的技术? comsci 技术
         看美国那边的气候情况....我有个感觉...是不是要进入小冰期了?      那么在小冰期里面...我们的户外活动肯定会出现很多问题...在室内呆着的情况会非常多...怎么在室内呆着而不发闷...怎么用最低的电力保证室内的温度.....这都需要技术手段...   &nb
  • js 获取浏览器型号 cuityang js浏览器
    根据浏览器获取iphone和apk的下载地址 <!DOCTYPE html> <html> <head>     <meta charset="utf-8" content="text/html"/>     <meta name=
  • C# socks5详解 转 dalan_123 socketC#
    http://www.cnblogs.com/zhujiechang/archive/2008/10/21/1316308.html  这里主要讲的是用.NET实现基于Socket5下面的代理协议进行客户端的通讯，Socket4的实现是类似的，注意的事，这里不是讲用C#实现一个代理服务器，因为实现一个代理服务器需要实现很多协议，头大，而且现在市面上有很多现成的代理服务器用，性能又好，
  • 运维 Centos问题汇总 dcj3sjt126com 云主机
    一、sh 脚本不执行的原因 sh脚本不执行的原因 只有2个 1.权限不够 2.sh脚本里路径没写完整。   二、解决You have new mail in /var/spool/mail/root 修改/usr/share/logwatch/default.conf/logwatch.conf配置文件 MailTo = MailFrom   三、查询连接数
  • Yii防注入攻击笔记 dcj3sjt126com sqlWEB安全yii
    网站表单有注入漏洞须对所有用户输入的内容进行个过滤和检查，可以使用正则表达式或者直接输入字符判断，大部分是只允许输入字母和数字的，其它字符度不允许；对于内容复杂表单的内容，应该对html和script的符号进行转义替换：尤其是<,>,',"",&这几个符号 这里有个转义对照表： http://blog.csdn.net/xinzhu1990/articl
  • MongoDB简介[一] eksliang mongodbMongoDB简介
    MongoDB简介 转载请出自出处：http://eksliang.iteye.com/blog/2173288 1.1易于使用        MongoDB是一个面向文档的数据库，而不是关系型数据库。与关系型数据库相比，面向文档的数据库不再有行的概念，取而代之的是更为灵活的“文档”模型。        另外，不
  • zookeeper windows 入门安装和测试 greemranqq zookeeper安装分布式
    一、序言       以下是我对zookeeper 的一些理解：      zookeeper 作为一个服务注册信息存储的管理工具，好吧，这样说得很抽象，我们举个“栗子”。       栗子1号：       假设我是一家KTV的老板，我同时拥有5家KTV，我肯定得时刻监视
  • Spring之使用事务缘由(2-注解实现) ihuning spring
      Spring事务注解实现   1. 依赖包：     1.1 spring包：           spring-beans-4.0.0.RELEASE.jar           spring-context-4.0.0.
  • iOS App Launch Option 啸笑天 option
    iOS 程序启动时总会调用application:didFinishLaunchingWithOptions:，其中第二个参数launchOptions为NSDictionary类型的对象，里面存储有此程序启动的原因。   launchOptions中的可能键值见UIApplication Class Reference的Launch Options Keys节 。 1、若用户直接
  • jdk与jre的区别（_） macroli javajvmjdk
    简单的说JDK是面向开发人员使用的SDK，它提供了Java的开发环境和运行环境。SDK是Software Development Kit 一般指软件开发包，可以包括函数库、编译程序等。  JDK就是Java Development Kit JRE是Java Runtime Enviroment是指Java的运行环境，是面向Java程序的使用者，而不是开发者。 如果安装了JDK，会发同你
  • Updates were rejected because the tip of your current branch is behind qiaolevip 学习永无止境每天进步一点点众观千象git
    $ git push joe prod-2295-1 To [email protected]:joe.le/dr-frontend.git ! [rejected] prod-2295-1 -> prod-2295-1 (non-fast-forward) error: failed to push some refs to '[email protected]
  • [一起学Hive]之十四-Hive的元数据表结构详解 superlxw1234 hivehive元数据结构
    关键字：Hive元数据、Hive元数据表结构   之前在 “[一起学Hive]之一–Hive概述，Hive是什么”中介绍过，Hive自己维护了一套元数据，用户通过HQL查询时候，Hive首先需要结合元数据，将HQL翻译成MapReduce去执行。 本文介绍一下Hive元数据中重要的一些表结构及用途，以Hive0.13为例。   文章最后面，会以一个示例来全面了解一下，
  • Spring 3.2.14，4.1.7，4.2.RC2发布 wiselyman Spring 3
      Spring 3.2.14、4.1.7及4.2.RC2于6月30日发布。   其中Spring 3.2.1是一个维护版本(维护周期到2016-12-31截止)，后续会继续根据需求和bug发布维护版本。此时，Spring官方强烈建议升级Spring框架至4.1.7 或者将要发布的4.2 。   其中Spring 4.1.7主要包含这些更新内容。
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他