《算法竞赛进阶指南》2.8IDAstar

IDA*
迭代加深版的A*算法
设计一个估计函数f（state）<= 真实步数

迭代加深基本框架：
depth = 0
while(!def(0, depth)) depth ++;

bool dfs()
{
	if(now_depth + f() > max_depth) return false;
}

180. 排书

给定n本书，编号为1-n。
在初始状态下，书是任意排列的。
在每一次操作中，可以抽取其中连续的一段，再把这段插入到其他某个位置。
我们的目标状态是把书按照1-n的顺序依次排列。
求最少需要多少次操作。

输入格式
第一行包含整数T，表示共有T组测试数据。
每组数据包含两行，第一行为整数n，表示书的数量。
第二行为n个整数，表示1-n的一种任意排列。
同行数之间用空格隔开。

输出格式
每组数据输出一个最少操作次数。
如果最少操作次数大于或等于5次，则输出”5 or more”。
每个结果占一行。

数据范围
1≤n≤15

输入样例：
3
6
1 3 4 6 2 5
5
5 4 3 2 1
10
6 8 5 3 4 7 2 9 1 10

输出样例：
2
3
5 or more

/*
1 2 3 4 5 6

连续k个，一共有n - k + 1种选法，总共有 n - k 种放法

总共有 (15 * 14 + 14 * 13 + .. + 2 * 1) / 2 有重复一样的放法 除以2 共560种操作

复杂度560^4, IDA*优化， 双向bfs
考虑估价函数: 每次操作会断开三个连接，然后引入三个连接。即每次操作最多会将三个连接修正。
求n - 1 中有多少个错误的连接（后一个数比前一个数大1的判断条件），记为tot 最少需要 tot/3 的下取整

估价函数: f(atate) = tot / 3 上取整

*/

#include 
#include 
#include 

using namespace std;

const int N = 15;

int n;
int q[N];
int w[5][N]; //辅助数组 交换操作

int f()
{
    int tot = 0;
    for(int i = 0; i + 1 < n; i ++)
        if(q[i + 1] != q[i] + 1)
            tot ++;
    return (tot + 2) / 3; //等价于(tot + 2) / 3 下取整         
    
}

bool check()
{
    for(int i = 0; i < n; i ++)
        if(q[i] != i + 1)
            return false;
    return true;        
}


bool dfs(int depth, int max_depth)
{
    if(depth + f() > max_depth) return false;
    if(check()) return true;
    
    //搜索每个分支 先枚举长度再枚举起点
    for(int len = 1; len <= n; len ++)
        for(int l = 0; l + len - 1 < n; l ++)
        {
            int r = l + len - 1;//当前段的右边
            for(int k = r + 1; k < n; k ++) //往前放和往后放的情况一样，可以规定往后放 从r + 1 开始枚举
            {
                memcpy(w[depth], q, sizeof q);
                int x, y;
                for(x = r + 1, y = l; x <= k; x ++, y ++) q[y] = w[depth][x];
                for(x = l; x <= r; x ++, y ++) q[y] = w[depth][x];
                if(dfs(depth + 1, max_depth)) return true;
                memcpy(q, w[depth], sizeof q);
            }
        }
    
    
    return false;
}

int main ()
{
    int T;
    scanf("%d", &T);
    while(T --)
    {
        scanf("%d", &n);
        for(int i = 0; i < n; i ++) scanf("%d", &q[i]);
        
        int depth = 0;
        while(depth < 5 && !dfs(0, depth)) depth ++; //迭代加深
        
        if(depth >= 5) puts("5 or more");
        else printf("%d\n", depth);
    }
    
    
    return 0;
}

181. 回转游戏

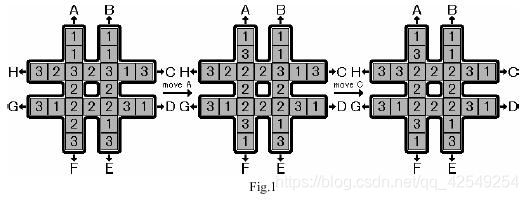
如下图所示，有一个“#”形的棋盘，上面有1,2,3三种数字各8个。
给定8种操作，分别为图中的A~H。
这些操作会按照图中字母和箭头所指明的方向，把一条长为8的序列循环移动1个单位。
例如下图最左边的“#”形棋盘执行操作A后，会变为下图中间的“#”形棋盘，再执行操作C后会变成下图最右边的“#”形棋盘。
给定一个初始状态，请使用最少的操作次数，使“#”形棋盘最中间的8个格子里的数字相同。

输入格式
输入包含多组测试用例。
每个测试用例占一行，包含24个数字，表示将初始棋盘中的每一个位置的数字，按整体从上到下，同行从左到右的顺序依次列出。
输入样例中的第一个测试用例，对应上图最左边棋盘的初始状态。
当输入只包含一个“0”的行时，表示输入终止。

输出格式
每个测试用例输出占两行。
第一行包含所有移动步骤，每步移动用大写字母“A~G”中的一个表示，字母之间没有空格，如果不需要移动则输出“No moves needed”。
第二行包含一个整数，表示移动完成后，中间8个格子里的数字。
如果有多种方案，则输出字典序最小的解决方案。

输入样例：
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0

输出样例：
AC
2
DDHH
2

/*
IDA*

考虑估价函数：
中间出现次数最多的数字设为k
每次操作，最多会加入一个相同的数，最少需要8 - k次操作

估价函数： f(state) = 8 - k

剪枝：避免枚举和上次相反的操作

如何得到最小字典序?
按照字典序最小来搜索，就会得到字典序最小的方案

          0     1
          2     3
    4  5  6  7  8  9  10
          11    12
    13 14 15 16 17 18 19
          20    21
          22    23

*/

#include 
#include 
#include 

using namespace std;

const int N = 24;

int op[8][7] = {
    {0, 2, 6, 11, 15, 20, 22},
    {1, 3, 8, 12, 17, 21, 23},
    {10, 9, 8, 7, 6, 5, 4},
    {19, 18, 17, 16, 15, 14, 13},
    {23, 21, 17, 12, 8, 3, 1},
    {22, 20, 15, 11, 6, 2, 0},
    {13, 14, 15, 16, 17, 18, 19},
    {4, 5, 6, 7, 8, 9, 10}
};

int opposite[8] = {5, 4, 7, 6, 1, 0, 3, 2};
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};

int q[N];
int path[100];

int f()
{
    static int sum[4];
    memset(sum, 0, sizeof sum);
    for(int i = 0; i < 8; i++) sum[q[center[i]]] ++;
    int s = 0;
    for(int i = 1; i <= 3; i ++) s = max(s, sum[i]);
    return 8 - s;
}

bool check()
{
    for(int i = 1; i < 8; i++)
        if(q[center[i]] != q[center[0]])
            return false;
    return true;        
}

void operate(int x)
{
    int t = q[op[x][0]];
    for(int i = 0; i < 6; i ++) q[op[x][i]] = q[op[x][i + 1]];
    q[op[x][6]] = t;
}

bool dfs(int depth, int max_depth, int last) //上一个操作
{
    if(depth + f() > max_depth) return false;
    if(check()) return true;
    
    // 扩展分支
    for(int i = 0; i < 8; i++)
    {
        if(opposite[i] == last) continue;
        operate(i);
        path[depth] = i;
        if(dfs(depth + 1, max_depth, i)) return true;
        operate(opposite[i]);
    }
    
    return false;
}


int main()
{
    while(scanf("%d", &q[0]), q[0])
    {
        for(int i = 1; i < N; i++) scanf("%d", &q[i]);
        
        int depth = 0;
        while(!dfs(0, depth, -1)) depth ++;
        
        if(!depth) printf("No moves needed");
        else
        {
            for(int i = 0; i < depth; i++) printf("%c", path[i] + 'A');
            
        }
        printf("\n%d\n", q[6]);
    }
    
    return 0;
}

182. 破坏正方形

下图左侧显示了一个用24根火柴棍构成的完整3×3网格。
所有火柴的长度都是1。
您可以在网格中找到许多不同大小的正方形。
在左图所示的网格中，有9个边长为1的正方形，4个边长为2的正方形和1个边长为3的正方形。
组成完整网格的每一根火柴都有唯一编号，该编号从上到下，从左到右，从1开始按顺序分配。
如果你将一些火柴棍从完整网格中取出，形成一个不完整的网格，则一部分正方形将被破坏。
右图为移除编号12,17和23的三个火柴棍后的不完整的3×3网格。
这次移除破坏了5个边长为1的正方形，3个边长为2的正方形和1个边长为3的正方形。
此时，网格不具有边长为3的正方形，但仍然具有4个边长为1的正方形和1个边长为2的正方形。

现在给定一个（完整或不完整）的n×n（n不大于5）网格，求至少再去掉多少跟火柴棒，可以使得网格内不再含有任何尺寸的正方形。

输入格式
输入包含T组测试用例。
测试用例的数量T在输入文件的第一行中给出。
每个测试用例由两行组成：
第一行包含一个整数n，表示网格的规模大小。
第二行以非负整数k开头，表示所给网格相较完整的n×n网格所缺少的火柴杆数量，后跟k个整数表示所有缺少的火柴杆的具体编号。
注意，如果k等于零，则表示输入网格是完整的n×n网格。

输出格式
每个测试用例输出一个结果，表示破坏所有正方形，所需的去掉火柴棒的最小数量。
每个结果占一行。

输入样例：
2
2
0
3
3 12 17 23

输出样例：
3
3

/*

目标：从现有的火柴中，最少选择多少根火柴，可以使得每个正方形中都被至少选了一根火柴。

重复覆盖问题: 至少选择多少行，可以使得每一列至少有一个1。

搜索顺序：每次选择一个还没有被覆盖的正方形（选择最小的一个），枚举选择它上面的哪根火柴

估价函数：枚举每个正方形，如果当前正方形还是完整的，那么直接删掉它的所有边，只记删除一次。

*/

#include 
#include 
#include 
#include 

using namespace std;

const int N = 61;

int n, m;
vector<int> square[N];
bool st[N]; //每条边是不是删掉

bool check(vector<int> &sq)
{
    for(int i = 0; i < sq.size(); i++)
        if(st[sq[i]])
            return false;
    return true;
}

int f()
{
    static bool state[N];
    
    memcpy(state, st, sizeof st);
    
    int res = 0;
    for(int i = 0; i < m; i++)
    {
        vector<int> &sq = square[i];
        if(check(sq))
        {
            res ++;
            for(int j = 0; j < sq.size(); j++) st[sq[j]] = true;
        }
    }
    memcpy(st, state, sizeof st);
    
    return res;
}

bool dfs(int depth, int max_depth)
{
    if(depth + f() > max_depth) return false;
    
    for(int i = 0; i < m; i++)
    {
        vector<int> &sq = square[i];
        if(check(sq))
        {
            for(int j = 0; j < sq.size(); j ++)
            {
                int x = sq[j];
                st[x] = true;
                if(dfs(depth + 1, max_depth)) return true;
                st[x] = false;
            }
            
            
            return false;
        }
    }
    return true;
}

int main()
{
    int T;
    scanf("%d", &T);
    while(T --)
    {
        scanf("%d", &n);
        
        memset(st, 0, sizeof st);
        
        m = 0;
        for(int len = 1; len <= n; len ++)
            for(int a = 1; a + len - 1 <= n; a ++)
                for(int b = 1; b + len - 1 <= n; b ++)
                {
                    auto &sq = square[m];
                    sq.clear();
                    int d = 2 * n + 1;
                    for(int i = 0; i < len; i++) //上下左右
                    {
                        sq.push_back(1 + (a - 1) * d + b - 1 + i);
                        sq.push_back(1 + (a + len - 1) * d + b - 1 + i);
                        sq.push_back(n + 1 + (a - 1) * d + b - 1 + i * d);
                        sq.push_back(n + 1 + (a - 1) * d + b - 1 + i * d + len);
                    }
                    m ++;
                }
        //for(int i = 0; i < m; i ++)
        //{
        //    for(auto x : square[i]) cout << x << ' ';
        //    cout << endl;
        //}
                
        int k = 0; 
        scanf("%d", &k);
        while(k --)
        {
            int x; 
            scanf("%d", &x);
            st[x] = true;
        }
        
        //puts("");
        int depth = 0;
        while(!dfs(0, depth)) depth ++;
        printf("%d\n", depth);
        
    }        
    
    return 0;
}