- 数学与算法设计:从理论到实践的路径
金枝玉叶9
程序员知识储备1程序员知识储备2程序员知识储备3算法机器学习人工智能数学建模数据库
随着科技的飞速发展,数学与算法设计在各个领域中的应用愈加广泛。从基础的计算机科学到复杂的人工智能系统,数学和算法无处不在,发挥着关键作用。本篇文章将深入探讨数学与算法设计的核心原理、发展趋势、经典案例以及从理论到实践的实现路径,帮助读者理解如何将理论知识转化为实际应用。一、数学与算法设计的核心原理在算法设计中,数学是其基础,而算法的优化则依赖于数学模型的精确表达。通常,我们通过以下几个方面进行优化
- 人工智能(AI)系统化学习路线
xiaoyu❅
python人工智能学习
一、为什么需要系统化学习AI?人工智能技术正在重塑各行各业,但许多初学者容易陷入误区:❌盲目跟风:直接学习TensorFlow/PyTorch,忽视数学与算法基础。❌纸上谈兵:只看理论不写代码,无法解决实际问题。❌方向模糊:对CV/NLP/RL等细分领域缺乏认知,难以针对性提升。正确的学习姿势:“金字塔式”分层学习(理论→算法→框架→应用→工程化),逐步构建完整的AI知识体系。二、人工智能学习路线
- 零基础学人工智能:TensorFlow 入门例子
人工智能MOS
人工智能tensorflowpython
识别手写图片因为这个例子是TensorFlow官方的例子,不会说的太详细,会加入了一点个人的理解,因为TensorFlow提供了各种工具和库,帮助开发人员构建和训练基于神经网络的模型。TensorFlow中最重要的概念是张量(Tensor),它代表了多维数组或矩阵,因此TensorFlow支持各种不同类型的计算,如线性回归、逻辑回归、卷积神经网络、循环神经网络等。所以帮我们极大减少了对数学与算法基
- C++ 数学与算法系列之高斯消元法求解线性方程组
一枚大果壳
C++编程之美算法c++线性代数
1.前言什么是消元法?消元法是指将多个方程式组成的方程组中的若干个变量通过有限次地变换,消去方程式中的变量,通过简化方程式,从而获取结果的一种解题方法。消元法主要有代入消元法、加减消元法、整体消元法、换元消元法、构造消元法、因式分解消元法、常数消元法、利用比例性质消元法等。对方程式消元时,是基于如下的初等行变换规则:改变方程组中方程式的顺序,或者说无论先求解方程组中哪一个方程式,不影响方程组的解。
- C++ 数学与算法系列之牛顿、二分迭代法求解非线性方程
一枚大果壳
C++编程之美算法python
1.前言前文介绍了如何使用“高斯消元法”求解线性方程组。本文秉承有始有终的态度,继续介绍“非线性方程”的求解算法。本文将介绍2个非线性方程算法:牛顿迭代法。二分迭代法。牛顿迭代法(Newton'smethod)又称为牛顿-拉夫逊方法(Newton-Raphsonmethod),是拉夫逊和牛顿同时提出来的一种在实数域和复数域上近似求解方程的方法。为何说是近似求解方程?因为对于多数方程式,因不存在求根
- 【数学与算法】【分段三次Hermite插值】和【分段三次样条插值】
Mister Zhu
数学和算法插值
光滑曲线在数学上的定义是什么??原文链接:光滑曲线在数学上的定义是什么?回答1:定义:切线随切点的移动而连续转动。若函数f(x)f(x)f(x)在区间(a,b)(a,b)(a,b)内具有一阶连续导数,则其图形为一条处处有切线的曲线。则为光滑曲线。简言之,若f′(x)f'(x)f′(x)连续,则曲线光滑。但反之,不成立。比如圆,圆在直角坐标系下,有两条竖直的切线,导数不存在(为∞大)。回答2:不敢保
- 【数学与算法】跟踪、预测、单目标、多目标、匈牙利匹配之间的关系
Mister Zhu
数学和算法自动驾驶算法
关于多目标跟踪的文章可以参考目标跟踪初探——SORT。多目标跟踪的步骤先后(简单记法):先预测,再匈牙利匹配,最后再卡尔曼预测矫正,得到最优估计。【卡尔曼预测+匈牙利匹配】进行多目标跟踪的详细步骤:(1)根据预测方程,计算【状态预测值(先验值)】、【状态误差协方差先验估计】;(2)计算每个检测对象与每个状态跟踪器之间的【代价矩阵】;(3)匈牙利匹配(KM算法)求出【检测对象和跟踪器的匹配对】、【未
- 【数学与算法】PCA主成分分析与降维的通俗理解
Mister Zhu
数学和算法pca降维
1.PCA与降维PCA主成分分析简单的理解,就是把某物的很多个能直接获取到的特征,经过变换得到很多个新特征,所有的新特征就是该物的成分。这些新特征对该物体来说,有的影响很大,有的影响很小,只需要使用这些影响大的新特征,舍弃很多影响小的新特征,就是使用主要的一些成分来分析,舍弃不重要的成分,这就是主成分分析的方法。相当于把特征维度给降低了,所以也叫降维。2.举例例如,假如我们想要用新方法衡量一个学生
- 【数学与算法】非线性最小二乘法的解法【最速梯度下降法】、【牛顿法】、【高斯牛顿法】、【LM算法】
Mister Zhu
数学和算法算法最小二乘法人工智能
关于非线性优化的问题,可以推荐观看视觉SLAM十四讲视频的第六讲非线性优化。如果不明白线性和非线性,可参考这篇博客:线性最小二乘和非线性最小二乘这篇博客的后面有讲到几种优化方法(最速梯度下降法、牛顿法、高斯牛顿法,LM算法),很容易记住,不像其他的公式推导那么生硬:BundleAdjustment—即最小化重投影误差(高翔slam—第七讲)这篇博客也很棒非线性优化(高翔slam—第六讲)下图摘自非
- 【数学与算法】KMeans聚类代码
Mister Zhu
数学和算法聚类
KMeans聚类是根据各点距离聚类中心的距离来把所有点分类到不同类别的无监督算法。对于聚类,就是两点:1.分类所有样本点:遍历每个数据样本点,分别计算该样本点与K个聚类中心的距离,把该样本点的类别重新分类为距离最小的那一类。2.更新聚类中心:所有样本点都按第一步重新分类后,把各类别的点重新计算聚类中心(求平均值的方法),更新K个类别的聚类中心值。3.重复前面两步,直到聚类中心点更新幅度小于阈值,或
- 欧拉计划(project euler)最详细中文题解
metaquant
技术世界数学算法编程语言python
欧拉计划是一个在线解题网站,题目以各类数学问题为主,通常需要结合一定的数学与编程知识,写出适当的程序求解问题(详细介绍可以参见我的文章)。相比于力扣等刷题网站,欧拉计划上的题目有着更丰富的知识背景,在解答题目的过程中常能学习新的数学与算法知识,享受解题愉悦的同时也能颇有收获。在我的解题过程中,我尽量追求对每道题给出最优的解法,然后写文章把我的思路与代码记录下来。在每篇文章中,我首先将题目翻译成了中
- 编程新手导论
wangluozhangleilei
杂谈编程语言数据结构设计模式编译器算法
第二部分导论,这一部分主要是关于编程的导论,(要懂得一点思想具备一点常识)《设计,编码,,与软工》(编程与思想)这一章解释了三种思想,原语,抽象,组合,,和软件开发的二个重要过程,,软件工程的相关概念,是编程入门的关键(要懂得一点领域内的数学)《数学与算法》(编程与数学)计算机整个就是架构在数学上的,跟计算机平台实现,算法设计,,架构密切相关,,真正要深入编程,,,对数学的学习是必须的,,千万不要
- 有趣的算法(一):如何让有情人终成眷属
闻人翎悬
***算法与编程艺术***DataScience:统计学习有趣的算法
我的机器学习教程「美团」算法工程师带你入门机器学习以及「三分钟系列」数据结构与算法已经开始更新了,欢迎大家订阅~这篇专栏整合了这几年的算法知识,简单易懂,也将是我实体书的BLOG版。欢迎大家扫码关注微信公众号「图灵的猫」,除了有更多AI、算法、Python相关文章分享,还有免费的SSR节点和外网学习资料。其他平台(微信/知乎/B站)也是同名「图灵的猫」,不要迷路哦~数学与算法告诉我们,有情人必将终
- 老猪带你玩转自定义控件三——sai大神带我实现ios 8 时间滚轮控件
weixin_34302561
ios8的时间滚轮控件实现了扁平化,带来很好用户体验,android没有现成控件,小弟不才,数学与算法知识不过关,顾十分苦恼,幸好在github上找到sai大神实现代码,甚为欣喜,顾把学习这个控件点滴记录下来,分享给大家。项目原地址https://github.com/saiwu-bigkoo/Android-PickerView。ios8滚轮的效果:而sai大神控件的效果:哎,妈呀是不是效果95
- Android 实现 ios 滚轮效果
qq_26972449
Android基础学习——其它
转载自:博客园网址:http://www.cnblogs.com博客原文:http://www.cnblogs.com/manuosex/p/5032934.htmlios8的时间滚轮控件实现了扁平化,带来很好用户体验,android没有现成控件,小弟不才,数学与算法知识不过关,顾十分苦恼,幸好在github上找到sai大神实现代码,甚为欣喜,顾把学习这个控件点滴记录下来,分享给大家。项目原地址h
- Python趣味编程:从入门到人工智能 高清完整版免费下载Python基础教程免费电子书
Spade_King
点击获取书籍提取码:ija8内容简介本书是专门为青少年编写的零基础Python语言>编程人门教材,由浅人深、循序渐进地讲授Python语言编程知识,以解决问题为导向,培养青少年的编程思维。本书采用单元课程的形式编排内容,分为编程基础、数学与算法、游戏编程、人工智能四个单元,采用符合青少年认知水平的趣味案例进行教学,指导青少年使用编程的思维方式解决身边的问题,带领青少年迈进Python编程的奇妙世界
- 数学与算法的艺术
ACdreamers
基础数学
为了更好体现数学在计算机算法中的重要作用,我来介绍一些数学知识以及它们的应用。Contens1.秦九韶算法9.最小二乘法2.斯特林公式10.自守数3.外观数列4.整数拆分问题5.阿贝尔变换6.二项式反演7.马青公式8.艾森斯坦判别法1.秦九韶算法秦九韶算法是中国南宋时期数学家秦九韶提出的一种计算多项式的优化算法。在西方又被称为Horner算法。给定一个多项式,计算这个多项式的值。可以对这个多项式进
- 不明觉厉!Gitee大神们的算法/数学相关开源项目推荐
Gitee
GiteeGitee项目推荐算法数学开源项目
现在的大厂面试,算法似乎已经成为了必考项目。当大家的业务水平相近,谁的数学与算法基础更好,谁可能就会获得更好的机会。Gitee上也有一些数学算法的大牛,今天就为大家分享他们的开源项目,希望能给正在学习算法和数学的你有所帮助。1.mfcplot项目作者:rewine开源许可协议:MIT项目地址:https://gitee.com/rewine/mfcplotmfc数学函数曲线绘制程序。2.milvu
- 组合数学与算法题-排列组合篇
rosewind
前言之前刷过一些leetcode的题目,这学期修了组合数学这门课,让我感受颇多。课程上更关注的是数学上的解法,并没有讲到具体的用某种语言实现,并没有深入地讲为什么这样做就是对的。结合我的经验,想分享一下我的理解。leetcode31.下一个全排列31.下一个全排列2个关键点:下一个全排列比当前的大(字典序)增量要是最小的一些例子:1243->1324,要使1243更大,从右往左看,43已经是最大的
- python实现决策树实例
Realmhang
python机器学习
今天用python实现了一个决策树模型,python做机器学习有大量的库支持,简洁高效,没有深厚数学与算法基础的人也可以调用库来实现机器学习模型。当然大家想做好机器学习还是要好好积淀深厚的知识,只当调包侠能做的东西非常有限啊。本文是对经典的鸢尾花数据集做分类,大家需要下载sklearn、pandas、matplotlib、seaborn库,可以直接在pycharm中下载,另外鸢尾花数据集已经包含在
- 编程新手导论(转载)
扇子
第二部分导论,这一部分主要是关于编程的导论,(要懂得一点思想具备一点常识)《设计,编码,,与软工》(编程与思想)这一章解释了三种思想,原语,抽象,组合,,和软件开发的二个重要过程,,软件工程的相关概念,是编程入门的关键(要懂得一点领域内的数学)《数学与算法》(编程与数学)计算机整个就是架构在数学上的,跟计算机平台实现,算法设计,,架构密切相关,,真正要深入编程,,,对数学的学习是必须的,,千万不要
- 编程新手导论(转载)
叶广明_微信ye_guangming
面试编程语言数据结构设计模式编译器算法
第二部分导论,这一部分主要是关于编程的导论,(要懂得一点思想具备一点常识)《设计,编码,,与软工》(编程与思想)这一章解释了三种思想,原语,抽象,组合,,和软件开发的二个重要过程,,软件工程的相关概念,是编程入门的关键(要懂得一点领域内的数学)《数学与算法》(编程与数学)计算机整个就是架构在数学上的,跟计算机平台实现,算法设计,,架构密切相关,,真正要深入编程,,,对数学的学习是必须的,,千万不要
- Java 技术书籍大全
济南市民刘先生
java
前言本文档目前已收录277本Java相关领域经典技术书籍,从初级开发者到资深架构师,涵盖Java从业者的各个阶段。涵盖领域:Java入门书籍,Java基础及进阶书籍,框架与中间件,架构设计,设计模式,数学与算法,JVM周边语言,项目管理&领导力&流程,职业素养与个人成长,格局与视野,面试参考书等。入门书籍《明解Java》-豆瓣评分8.5《Java从入门到精通(第4版附光盘)》-豆瓣评分6《入门很简
- "歌美"之游戏开发之数学与算法_中级篇
小太阳会发光诺
ActionScript3.0是一种强大的面向对象编程语言,它还是一种适合快速构建效果丰富的互联网应用程序的语言,它所构建的应用程序已经成为Web体验的重要部分。本书以ActionScript为核心,辅以Photoshop等作为工具,深入剖析了图形图像算法及特性,介绍了游戏等特效的制作和实现,并且聚焦相关技术在交互程序各领域的应用。课程目录:课时1:概率问题与三角函数(1)课时2:概率问题与三角函
- "歌美"之游戏开发之数学与算法_高级篇
小太阳会发光诺
ActionScript3.0是一种强大的面向对象编程语言,它还是一种适合快速构建效果丰富的互联网应用程序的语言,它所构建的应用程序已经成为Web体验的重要部分。本书以ActionScript为核心,辅以Photoshop等作为工具,深入剖析了图形图像算法及特性,介绍了游戏等特效的制作和实现,并且聚焦相关技术在交互程序各领域的应用。课程目录:第1章:换元积分法和贝塞尔曲线积分的拟合课时1:换元积分
- 从入门到入坟:Java程序员一生要看多少书?Java技术书籍大全来啦
Java技术箭
Java程序员SpringBoot
本文档目前已收录277本Java相关领域经典技术书籍,从初级开发者到资深架构师,涵盖Java从业者的各个阶段,并持续更新。涵盖领域:Java入门书籍,Java基础及进阶书籍,框架与中间件,架构设计,设计模式,数学与算法,JVM周边语言,项目管理&领导力&流程,职业素养与个人成长,格局与视野,面试参考书等。注:本文只是推荐,只有一小部分的书籍有文档资料分享。包括:【Redis实战】【Kafka核心设
- Java 技术书籍大全
乐百氏vic
Java技术书籍大全本文档目前已收录277本Java相关领域经典技术书籍,从初级开发者到资深架构师,涵盖Java从业者的各个阶段。涵盖领域:Java入门书籍,Java基础及进阶书籍,框架与中间件,架构设计,设计模式,数学与算法,JVM周边语言,项目管理&领导力&流程,职业素养与个人成长,格局与视野,面试参考书等。入门书籍《明解Java》-豆瓣评分8.5《Java从入门到精通(第4版附光盘)》-豆瓣
- 80后博导拟任“211大学”副校长 曾是人大最年轻教授
机器学习算法与Python学习-公众号
本文转自“数学与算法之美”2012年,时年32岁的他成为中国人民大学最年轻的教授。6月20日,海南省委组织部发布干部任前公示,其中,现任中国人民大学汉青经济与金融高级研究院教授、反垄断与竞争政策研究所所长叶光亮拟任海南大学党委常委、副校长(试用期一年)。叶光亮温州新闻网图据公开简历,叶光亮是一名“80后”学者,生于1980年4月,研究生学历,经济学博士学位,教授,博士生导师,长江学者(青年)。叶光
- 数学与算法的艺术
K_ona
数学
为了更好体现数学在计算机算法中的重要作用,我来介绍一些数学知识以及它们的应用。转自:https://blog.csdn.net/acdreamersContens1.秦九韶算法9.最小二乘法2.斯特林公式10.自守数3.外观数列4.整数拆分问题5.阿贝尔变换6.二项式反演7.马青公式8.艾森斯坦判别法1.秦九韶算法秦九韶算法是中国南宋时期数学家秦九韶提出的一种计算多项式的优化算法。在西方又被称为H
- 老猪带你玩转自定义控件三——sai大神带我实现ios 8 时间滚轮控件
laozhu1124
ios8的时间滚轮控件实现了扁平化,带来很好用户体验,android没有现成控件,小弟不才,数学与算法知识不过关,顾十分苦恼,幸好在github上找到sai大神实现代码,甚为欣喜,顾把学习这个控件点滴记录下来,分享给大家。项目原地址https://github.com/saiwu-bigkoo/Android-PickerView。ios8滚轮的效果: 而sai大神控件的效果: 哎,妈呀是不是效果
- java的(PO,VO,TO,BO,DAO,POJO)
Cb123456
VOTOBOPOJODAO
转:
http://www.cnblogs.com/yxnchinahlj/archive/2012/02/24/2366110.html
-------------------------------------------------------------------
O/R Mapping 是 Object Relational Mapping(对象关系映
- spring ioc原理(看完后大家可以自己写一个spring)
aijuans
spring
最近,买了本Spring入门书:spring In Action 。大致浏览了下感觉还不错。就是入门了点。Manning的书还是不错的,我虽然不像哪些只看Manning书的人那样专注于Manning,但怀着崇敬 的心情和激情通览了一遍。又一次接受了IOC 、DI、AOP等Spring核心概念。 先就IOC和DI谈一点我的看法。IO
- MyEclipse 2014中Customize Persperctive设置无效的解决方法
Kai_Ge
MyEclipse2014
高高兴兴下载个MyEclipse2014,发现工具条上多了个手机开发的按钮,心生不爽就想弄掉他!
结果发现Customize Persperctive失效!!
有说更新下就好了,可是国内Myeclipse访问不了,何谈更新...
so~这里提供了更新后的一下jar包,给大家使用!
1、将9个jar复制到myeclipse安装目录\plugins中
2、删除和这9个jar同包名但是版本号较
- SpringMvc上传
120153216
springMVC
@RequestMapping(value = WebUrlConstant.UPLOADFILE)
@ResponseBody
public Map<String, Object> uploadFile(HttpServletRequest request,HttpServletResponse httpresponse) {
try {
//
- Javascript----HTML DOM 事件
何必如此
JavaScripthtmlWeb
HTML DOM 事件允许Javascript在HTML文档元素中注册不同事件处理程序。
事件通常与函数结合使用,函数不会在事件发生前被执行!
注:DOM: 指明使用的 DOM 属性级别。
1.鼠标事件
属性
- 动态绑定和删除onclick事件
357029540
JavaScriptjquery
因为对JQUERY和JS的动态绑定事件的不熟悉,今天花了好久的时间才把动态绑定和删除onclick事件搞定!现在分享下我的过程。
在我的查询页面,我将我的onclick事件绑定到了tr标签上同时传入当前行(this值)参数,这样可以在点击行上的任意地方时可以选中checkbox,但是在我的某一列上也有一个onclick事件是用于下载附件的,当
- HttpClient|HttpClient请求详解
7454103
apache应用服务器网络协议网络应用Security
HttpClient 是 Apache Jakarta Common 下的子项目,可以用来提供高效的、最新的、功能丰富的支持 HTTP 协议的客户端编程工具包,并且它支持 HTTP 协议最新的版本和建议。本文首先介绍 HTTPClient,然后根据作者实际工作经验给出了一些常见问题的解决方法。HTTP 协议可能是现在 Internet 上使用得最多、最重要的协议了,越来越多的 Java 应用程序需
- 递归 逐层统计树形结构数据
darkranger
数据结构
将集合递归获取树形结构:
/**
*
* 递归获取数据
* @param alist:所有分类
* @param subjname:对应统计的项目名称
* @param pk:对应项目主键
* @param reportList: 最后统计的结果集
* @param count:项目级别
*/
public void getReportVO(Arr
- 访问WEB-INF下使用frameset标签页面出错的原因
aijuans
struts2
<frameset rows="61,*,24" cols="*" framespacing="0" frameborder="no" border="0">
- MAVEN常用命令
avords
Maven库:
http://repo2.maven.org/maven2/
Maven依赖查询:
http://mvnrepository.com/
Maven常用命令: 1. 创建Maven的普通java项目: mvn archetype:create -DgroupId=packageName
- PHP如果自带一个小型的web服务器就好了
houxinyou
apache应用服务器WebPHP脚本
最近单位用PHP做网站,感觉PHP挺好的,不过有一些地方不太习惯,比如,环境搭建。PHP本身就是一个网站后台脚本,但用PHP做程序时还要下载apache,配置起来也不太很方便,虽然有好多配置好的apache+php+mysq的环境,但用起来总是心里不太舒服,因为我要的只是一个开发环境,如果是真实的运行环境,下个apahe也无所谓,但只是一个开发环境,总有一种杀鸡用牛刀的感觉。如果php自己的程序中
- NoSQL数据库之Redis数据库管理(list类型)
bijian1013
redis数据库NoSQL
3.list类型及操作
List是一个链表结构,主要功能是push、pop、获取一个范围的所有值等等,操作key理解为链表的名字。Redis的list类型其实就是一个每个子元素都是string类型的双向链表。我们可以通过push、pop操作从链表的头部或者尾部添加删除元素,这样list既可以作为栈,又可以作为队列。
&nbs
- 谁在用Hadoop?
bingyingao
hadoop数据挖掘公司应用场景
Hadoop技术的应用已经十分广泛了,而我是最近才开始对它有所了解,它在大数据领域的出色表现也让我产生了兴趣。浏览了他的官网,其中有一个页面专门介绍目前世界上有哪些公司在用Hadoop,这些公司涵盖各行各业,不乏一些大公司如alibaba,ebay,amazon,google,facebook,adobe等,主要用于日志分析、数据挖掘、机器学习、构建索引、业务报表等场景,这更加激发了学习它的热情。
- 【Spark七十六】Spark计算结果存到MySQL
bit1129
mysql
package spark.examples.db
import java.sql.{PreparedStatement, Connection, DriverManager}
import com.mysql.jdbc.Driver
import org.apache.spark.{SparkContext, SparkConf}
object SparkMySQLInteg
- Scala: JVM上的函数编程
bookjovi
scalaerlanghaskell
说Scala是JVM上的函数编程一点也不为过,Scala把面向对象和函数型编程这两种主流编程范式结合了起来,对于熟悉各种编程范式的人而言Scala并没有带来太多革新的编程思想,scala主要的有点在于Java庞大的package优势,这样也就弥补了JVM平台上函数型编程的缺失,MS家.net上已经有了F#,JVM怎么能不跟上呢?
对本人而言
- jar打成exe
bro_feng
java jar exe
今天要把jar包打成exe,jsmooth和exe4j都用了。
遇见几个问题。记录一下。
两个软件都很好使,网上都有图片教程,都挺不错。
首先肯定是要用自己的jre的,不然不能通用,其次别忘了把需要的lib放到classPath中。
困扰我很久的一个问题是,我自己打包成功后,在一个同事的没有装jdk的电脑上运行,就是不行,报错jvm.dll为无效的windows映像,如截图
最后发现
- 读《研磨设计模式》-代码笔记-策略模式-Strategy
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
策略模式定义了一系列的算法,并将每一个算法封装起来,而且使它们还可以相互替换。策略模式让算法独立于使用它的客户而独立变化
简单理解:
1、将不同的策略提炼出一个共同接口。这是容易的,因为不同的策略,只是算法不同,需要传递的参数
- cmd命令值cvfM命令
chenyu19891124
cmd
cmd命令还真是强大啊。今天发现jar -cvfM aa.rar @aaalist 就这行命令可以根据aaalist取出相应的文件
例如:
在d:\workspace\prpall\test.java 有这样一个文件,现在想要将这个文件打成一个包。运行如下命令即可比如在d:\wor
- OpenJWeb(1.8) Java Web应用快速开发平台
comsci
java框架Web项目管理企业应用
OpenJWeb(1.8) Java Web应用快速开发平台的作者是我们技术联盟的成员,他最近推出了新版本的快速应用开发平台 OpenJWeb(1.8),我帮他做做宣传
OpenJWeb快速开发平台以快速开发为核心,整合先进的java 开源框架,本着自主开发+应用集成相结合的原则,旨在为政府、企事业单位、软件公司等平台用户提供一个架构透
- Python 报错:IndentationError: unexpected indent
daizj
pythontab空格缩进
IndentationError: unexpected indent 是缩进的问题,也有可能是tab和空格混用啦
Python开发者有意让违反了缩进规则的程序不能通过编译,以此来强制程序员养成良好的编程习惯。并且在Python语言里,缩进而非花括号或者某种关键字,被用于表示语句块的开始和退出。增加缩进表示语句块的开
- HttpClient 超时设置
dongwei_6688
httpclient
HttpClient中的超时设置包含两个部分:
1. 建立连接超时,是指在httpclient客户端和服务器端建立连接过程中允许的最大等待时间
2. 读取数据超时,是指在建立连接后,等待读取服务器端的响应数据时允许的最大等待时间
在HttpClient 4.x中如下设置:
HttpClient httpclient = new DefaultHttpC
- 小鱼与波浪
dcj3sjt126com
一条小鱼游出水面看蓝天,偶然间遇到了波浪。 小鱼便与波浪在海面上游戏,随着波浪上下起伏、汹涌前进。 小鱼在波浪里兴奋得大叫:“你每天都过着这么刺激的生活吗?简直太棒了。” 波浪说:“岂只每天过这样的生活,几乎每一刻都这么刺激!还有更刺激的,要有潮汐变化,或者狂风暴雨,那才是兴奋得心脏都会跳出来。” 小鱼说:“真希望我也能变成一个波浪,每天随着风雨、潮汐流动,不知道有多么好!” 很快,小鱼
- Error Code: 1175 You are using safe update mode and you tried to update a table
dcj3sjt126com
mysql
快速高效用:SET SQL_SAFE_UPDATES = 0;下面的就不要看了!
今日用MySQL Workbench进行数据库的管理更新时,执行一个更新的语句碰到以下错误提示:
Error Code: 1175
You are using safe update mode and you tried to update a table without a WHERE that
- 枚举类型详细介绍及方法定义
gaomysion
enumjavaee
转发
http://developer.51cto.com/art/201107/275031.htm
枚举其实就是一种类型,跟int, char 这种差不多,就是定义变量时限制输入的,你只能够赋enum里面规定的值。建议大家可以看看,这两篇文章,《java枚举类型入门》和《C++的中的结构体和枚举》,供大家参考。
枚举类型是JDK5.0的新特征。Sun引进了一个全新的关键字enum
- Merge Sorted Array
hcx2013
array
Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
Note:You may assume that nums1 has enough space (size that is
- Expression Language 3.0新特性
jinnianshilongnian
el 3.0
Expression Language 3.0表达式语言规范最终版从2013-4-29发布到现在已经非常久的时间了;目前如Tomcat 8、Jetty 9、GlasshFish 4已经支持EL 3.0。新特性包括:如字符串拼接操作符、赋值、分号操作符、对象方法调用、Lambda表达式、静态字段/方法调用、构造器调用、Java8集合操作。目前Glassfish 4/Jetty实现最好,对大多数新特性
- 超越算法来看待个性化推荐
liyonghui160com
超越算法来看待个性化推荐
一提到个性化推荐,大家一般会想到协同过滤、文本相似等推荐算法,或是更高阶的模型推荐算法,百度的张栋说过,推荐40%取决于UI、30%取决于数据、20%取决于背景知识,虽然本人不是很认同这种比例,但推荐系统中,推荐算法起的作用起的作用是非常有限的。
就像任何
- 写给Javascript初学者的小小建议
pda158
JavaScript
一般初学JavaScript的时候最头痛的就是浏览器兼容问题。在Firefox下面好好的代码放到IE就不能显示了,又或者是在IE能正常显示的代码在firefox又报错了。 如果你正初学JavaScript并有着一样的处境的话建议你:初学JavaScript的时候无视DOM和BOM的兼容性,将更多的时间花在 了解语言本身(ECMAScript)。只在特定浏览器编写代码(Chrome/Fi
- Java 枚举
ShihLei
javaenum枚举
注:文章内容大量借鉴使用网上的资料,可惜没有记录参考地址,只能再传对作者说声抱歉并表示感谢!
一 基础 1)语法
枚举类型只能有私有构造器(这样做可以保证客户代码没有办法新建一个enum的实例)
枚举实例必须最先定义
2)特性
&nb
- Java SE 6 HotSpot虚拟机的垃圾回收机制
uuhorse
javaHotSpotGC垃圾回收VM
官方资料,关于Java SE 6 HotSpot虚拟机的garbage Collection,非常全,英文。
http://www.oracle.com/technetwork/java/javase/gc-tuning-6-140523.html
Java SE 6 HotSpot[tm] Virtual Machine Garbage Collection Tuning
&
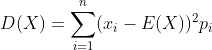 为随机变量X的方差。
为随机变量X的方差。