线段树(递归+二分的漩涡)
首先放出大佬的博客,写的很好,对每个函数的理解都很清晰,大佬
首先说一下线段树的数组范围是4*N(这个N是区间的长度),这个由来是一个博客,好像是一个二叉树的什么性质,就这样这个数组范围就这样定了,有的错误就是数组范围太小了,导致一些溢出错误,所以数组开大点就不会溢出了。假设根的高度为1的话,树的最大高度为![]() (n>1)(是向下取整,就是舍弃掉小数点),然后使用等比数列的公式,2^k-1(k是高度),就可以得出数组下标范围了,就是 4*N-5,所以我们直接开 4*N的范围就可以了。
(n>1)(是向下取整,就是舍弃掉小数点),然后使用等比数列的公式,2^k-1(k是高度),就可以得出数组下标范围了,就是 4*N-5,所以我们直接开 4*N的范围就可以了。
线段树可以处理很多的问题,一些区间可加性问题比如,
符合区间加法的例子:
数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和
最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );
最大值——总最大值=max(左区间最大值,右区间最大值),等等都是区间可加性问题。
下面先从最简单的建立线段树开始,建立线段树可以使用数组来建立,或者使用链表来建立(因为本身就是二叉树,所以可以使用二叉树的链表来建立线段树),我放出代码:
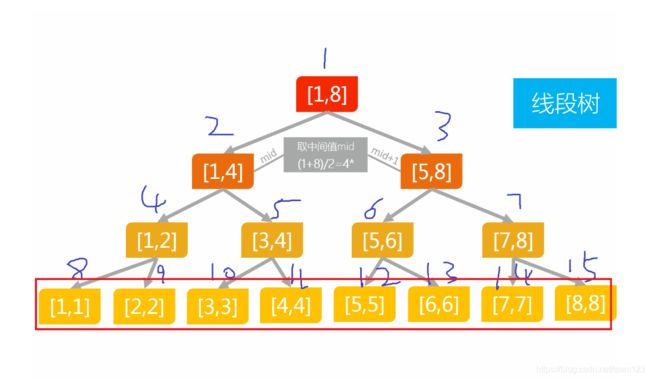
本身线段树就是一个二叉树,所以我们就需要二分的思想,分为左子区间和又子区间两块,每一块我们还可以再去分为左子区间和又子区间,就是一个二分的思想,就是下面这个图所呈现的,虽然名字是线段树,但是还是一个点来表示一段区间,但是这个点是代表着一段区间的意思,就像[1,8] 当做1节点,它是从1节点到8节点的区间和(这个是所要求的因素的和,比如加法和,GCD,最大值,最小值等),我们就是用这种方法来模拟一段段的区间。
线段树的结构
线段树先是由一个大区间组成,然后二分区间将区间逐渐缩小,[l,(l+r)/2] 为左子区间 ,[(l+r)/2+1,r]为右子区间,按照二叉树的样子逐渐将区间二分,一直到一个区间长度为1的时候 [1,1],[2,2],[3,3]等 像这种的子区间就停止了,其实原始数据都在这些子叶节点上,上面的一些区间节点就是一些节点的加和(不只是加法之和)。
建立线段树
1.数组的形式,因为有一层一层的结构,区间可以分成为很多的段,我们就可以使用递归来建立线段树,数组下标 t*2是左子树,t*2+1 是右子树,然后逐渐的将区间 [1,n]分为很多的段,使用递归是最好的选择了(其实我不会非递归的写法)。递归很像建立二叉树时候的操作,按照前序的方式来建树(实质就是用递归的操作,先建立左子树,再建立右子树) ,就是下面这个操作:
//数组建立线段树
#include
#include
const int maxn=1005;
const int inf=(1<<30);
typedef long long ll;
using namespace std;
int t[maxn*4];
int a[maxn]; //原数组
queueq;
//建树求和 数组t
void build(int now,int l,int r)
{
if(l>=r)
{
t[now]=a[l];
return;
}
int mid=(l+r)/2;
build(now<<1 , l , mid);
build(now<<1|1 , mid+1 , r);
t[now]=t[now<<1]+t[now<<1|1];
}
//DFS 前序遍历输出测试数据
void dfs(int now,int l,int r)
{
if(l>=r)
{
cout<>n;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
dfs(1,1,n);
return 0;
} 还有链表的形式来建立线段树。就是开出左右孩子节点,实质还是递归的实质,只是没有用到下标来找左子树和右子树,代码:
//链表建立线段树
#include
#include
#include
#include
#include
const int maxn = 1005;
const int inf = (1 << 30);
typedef long long ll;
using namespace std;
int a[maxn];
typedef struct node
{
int data;
struct node *left;
struct node *right;
}point;
point *creat(int l, int r)
{
point *p;
p = (point*)malloc(sizeof(point));
if (l >= r)
{
p->data = a[l];
p->left = p->right = NULL;
}
else
{
int mid = (l + r) / 2;
p->left = creat(l, mid);
p->right = creat(mid + 1, r);
p->data = p->left->data + p->right->data;
}
return p;
}
//先左后右的输出方式,类似于前序遍历
void dfs1(point *root)
{
if (root)
{
cout << root->data << endl;
dfs1(root->left);
dfs1(root->right);
}
}
int k=0;
int now=0;
//层次遍历
void dfs2(point *root)
{
queueq;
q.push(root);
while (!q.empty())
{
point *t = q.front();
q.pop();
cout << t->data << ' ';
if(now>=2*k)
{
k++;
cout<left)
q.push(t->left);
if (t->right)
q.push(t->right);
}
}
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
point *root;
root = creat(1, n);
dfs1(root); //输出方式一
cout << endl;
dfs2(root); //输出方式二
return 0;
}
还有结构体数组来建立二叉树
#include
#include
using namespace std;
const int maxn=1005;
struct node
{
int l,r;
int left,right;
int sum;
}t[maxn<<2];
int a[maxn];
void build(int now,int l,int r)
{
t[now].l=l;
t[now].r=r;
t[now].left=now<<1;
t[now].right=now<<1|1;
if(l>=r)
{
t[now].sum=a[l];
t[now].left=t[now].right=0;
return ;
}
else
{
int mid=(l+r)/2;
build(now<<1,l,mid);
build(now<<1|1,mid+1,r);
t[now].sum=t[now<<1].sum+t[now<<1|1].sum;
}
}
void dfs(int now)
{
if(t[now].l>=t[now].r)
{
cout<q;
q.push(now);
while(!q.empty())
{
int u=q.front();
q.pop();
cout<>n;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
dfs(1); //就是前序遍历
cout< 还是结构体数组的形式好写,直接下标t t*2 ,t*2+1 代表左子区间 和 右子区间,比链表操作简单,建议使用结构体来做,里面可以拥有很多的参数,l r ,left right ,还可以有mid ,lazy(懒惰标记,在下面会讲到,先别多想)。
单点修改
下面看看单点修改是个什么操作,我们已经建立好的线段树,可能也需要进行一些点的修改,那么怎么进行单点修改呢?我来说一下(可能有的不对,大神一定要指出啊,希望大佬不吝赐教)。我们现在知道要修改的点的位置和要进行修改的内容,这里面我们得需要一些二分的操作和思想了,跟一个区间修改只修改一个节点是一样的效果,但是这里的一些递归和二分操作还是需要理解和弄懂的;单点修改是区间修改的一个基础(我想的是这样),说一下单点修改。
首先弄懂一个事情,就是下面这张图中所体现的,在线段树数组中(就是这个结构体数组,保存着很多区间段的数据)的下标,这个下标就很多了,然后就是另一种下标真实数据的下标(这个是题目中的数据下标 1 2 3,与前面的线段树数组下标是不一样的),我们这里的单点修改,修改的就是真实数据的下标点,不是线段树数组的下标,这个得首先弄清楚,之后我们再介绍该怎么操作,其实与那个二分查找一样,逐渐分区间, 找到那个最终的叶子节点,进行修改之后,然后回溯进行整棵树的维护,更新权值(一个区间可能拥有已经修改的节点(真实数据的节点)),我们需要进行回溯更新权值:
举一个例子,就是我在[1,8]中修改节点 1的数据,我们需要用二分来找(毕竟线段树的下标不是真实数据的下标),在这里我们需要将对这个区间范围[1,8] 进行二分查找(这个范围中的数据就是真实数据的下标)。知道这个后,我们怎么找到在线段树数组中这个真实数据的下标呢?(为什么这么说呢?因为我们将数据一段一段的保存在区间中了,所以要想修改这个数据时,我们需要知道这个在线段树数组中的下标,这个时候,我们就需要进行二分查找,逐渐确定这个下标,然后进行修改)。就是上面这个分析。
代码:
index 是修改节点的位置 ,num 是要修改的数据,now 是从1开始的
void update(int num, int index, int now) //类似于二分查找
{
if (t[now].l >= t[now].r)
{
t[now].sum += num; //可以是替换操作
return;
}
int mid = (t[now].l + t[now].r) / 2; //二分操作
if (index <= mid)
update(num, index, now << 1); //去搜左子树
else
update(num, index, now << 1 | 1); //去搜右子树
t[now].sum = t[now << 1].sum + t[now << 1 | 1].sum; //线段树更新权值,使用回溯法
}就是这样子进行单点修改。在这里我们知道,我们进行单点修改的话,我们需要二分到最后那一个长度为1的区间(就是那个数据的区间),这样我们就将我们来使经过的节点都会更新权值(因为有回溯),所以经过单点修改后的线段树是完整的(没有哪一部分是还没有更新的),这个需要格外的注意,因为在下面的区间修改中,我们会进行一些优化,使得线段树在刚进行区间修改之后是没有完整的,等到我们需要这个更新完之后的值的时候,我们才加上去,这样减少了时间。这个区间修改下面会讲,现在不懂,有点蒙,可以理解。测试代码在最后,可以看看是不是对整棵树都进行了权值修改。
区间修改
我们知道需要修改的范围[a,b]后,我们从一开始的线段树节点1开始(范围是最大的那个区间)。首先我们从单点修改中已经知道,我们使用二分和递归逐渐找到那个点(是找到那个区间长度是1的区间),而区间修改是一个区间,我们得从左右两边两个方向开始,开始二分和递归,上面的单点修改已经说的很详细了,我直接放出代码:(在最后的测试代码中,有测试函数)
void update_range2(int now,int l,int r,int num)
{
if(t[now].l>=t[now].r)
{
t[now].sum+=num;
return ;
}
int mid=(t[now].l+t[now].r)/2;
if(l<=mid)
{
update_range2(now<<1,l,r,num);
}
if(midLazy数组思想和操作和区间修改优化(两者之间关系密切,就放到一起讲了)
//延迟数组
void push_down(int now, int l, int r)
{
if (lazy[now])
{
int mid = (l + r) / 2;
lazy[now << 1] += lazy[now];
lazy[now << 1 | 1] += lazy[now];
t[now << 1].sum += (mid - l + 1)*lazy[now];
t[now << 1 | 1].sum += (r - mid)*lazy[now];
lazy[now] = 0;
}
}
void update_range(int now, int l, int r, int num)
{
if (l <= t[now].l && r >= t[now].r)
{
lazy[now] += num;
t[now].sum += (t[now].r - t[now].l + 1)*num;
return;
}
push_down(now, t[now].l, t[now].r);
int mid = (t[now].l + t[now].r) / 2;
if (l <= mid)
update_range(now << 1, l, r, num);
if (r > mid)
update_range(now << 1 | 1, l, r, num);
t[now].sum = t[now << 1].sum + t[now << 1 | 1].sum;
}在讲区间修改和查询(单点和区间)之前,我们先讲一个优化。我先举一个例子,我们先这样想,题目要求我将一段区间上的数据都加上C,我们可以对这段区间上的每一个点进行单点修改,我们也可以将每一次的变化值都保存起来,我们等到再使用时,我们直接将这个变化值加上去就可以了;第一种一个一个修改,造成了很多的时间浪费,我们直接将这个变化值保存起来到每一个节点上(是线段树的下标节点),我们需要查询哪一个的时候,直接加上这个变化值就可以了。这样区间修改的优化版就出来了,节约了很多是时间。这个函数大佬们都叫做push_down ,延迟数组,我们需要重新开一个数组 lazy[maxn<<2],这个数组的范围也是要跟线段树的范围一样为节点的 4倍,才能保证不溢出。基本的原理是这样,我们的修改区间如果比现在所处的区间大的时候,我们就不需要再往下进行二分加递归了,我们就直接在这里就进行停止了,我们使用lazy 数组,将变化值记录下来,这个lazy数组也是二叉树的结构,也可以由一个节点传输数据到左子树或者右子树上,这样就连做一个串,只要给出一个开头,后面的数据我们都可以进行加上,所以一个lazy 数组就可以规避了一个完整的区间下许多叶子节点的时间消耗(这个完整的区间,就是完全被修改区间包围着,我们就可以直接对这个完整区间进行操作,记录下数据后,我们在数据查询的时候我们再利用这个数据)。在区间修改的没有优化的代码中,我们已经知道我们要对一开始的大区间进行二分操作逐渐分到每一个叶子区间上,在区间修改的优化上,我们只要找到那个合适的区间就可以了,我们不用再去找到那个叶子区间了,避免了很多的时间。下面就说一下这个完整的区间。
适合的区间
判断现在所处的区间是不是合适的,条件和原则和做法:(这个很重要)
1.修改区间完全与结点表示区间重合。此时,说明我们已经可以对该结点进行操作了。(就是直接进行数据更新)
2.修改区间在结点表示区间内。此时,说明现在的结点表示空间太大了,需要向下寻找更合适的区间。(我们缩小现在所处的区间 )
3.修改区间比结点表示区间大,只有向下推的时候才能出现这样的情况,跟第一种可能的结果一样,对结点进行操作就行了。
4.修改区间与结点表去区间只有一部分重合。只有向下推的时候才能出现这样的情况,跟第二种可能的结果一样,下推。
5.修改区间与结点表示区间完全不重合。无操作,等待程序自己结束。
就是上面这几种的情况,我们就可以按照每种的情况来做。
1.lazy 数组的结构
既然lazy 数组要保存线段树数组中对应的变化值,所以我们也要将lazy 数组看成线段树那样的二叉树结构,每一个节点都有左子树和右子树,这个lazy[ ]就是用来保存变化值的。到底如何使用到这个变化值,我们下面的单点查询和区间查询中会介绍到,现在只要求理解这个lazy 数组是干啥的,知道怎么使用就可以了,我们构造lazy 数组为二叉树的结构,就是使他可以往左子树,右子树的lazy 数组中传输数据,使得我们优化版的区间修改,在一个完整区间处把数据传给相应节点的 lazy 数组,在这个以下区间节点都可以得到这个lazy 数组传过来的数据。
2.lazy 数组的作用
push_down 函数在区间修改这里的作用是找到合适的区间,然后把数据加进去,然后将修改的数据保存下来;真正的作用是在数据查询的时候,保存在lazy数组中的数据会释放出来,加到这个节点的左子树和右子树上(因为这个区间内已经被修改区间包围了,我们就直接对左子树和右子树进行修改就行了,对于本节点的修改,直接在找到合适区间的时候就更新了)。好微妙。直接省掉了很多的递归和二分操作。这就是lazy数组在区间修改和查询中的作用。
3.lazy 数组的操作
我们在push_down函数中,如果当前节点的lazy 数组中有数据,不是0,我们就知道下面的左子树和右子树需要进行权值修改,我们就把这个数据标记传给左子树和右子树,相应的进行权值更新,并且将这个节点的lazy数组标记变为0,表示这个点已经更新过了,这样就可以把数据更新到一个完整区间的下面的左子树和右子树上,这样就是查询的时候push_down函数起到的作用,lazy 数组在查询时,数据传到了下面的树中,可谓起到了很大的作用。这操作牛逼。
4.区间修改中的操作
我们看一看那个区间修改的函数,只有我们找到合适的区间的时候,我们就停止二分操作了,我们的lazy[now] 数组才能储存到修改的变化值的 ,然后更新这个节点的权值:就是这个区间的长度Xnum(要加的数据),这个还是很好理解的吧,就是几个叶子节点一起要加上num,所以代码要这样写。
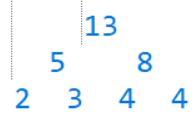
t[now].sum += (t[now].r - t[now].l + 1)*num;别的时候都是不能得到这个 lazy 变化值的,只要我们找到了合适的区间,这个区间往下的区间我们都不会再去递归二分找出更小的区间了,一定要注意这个push_down函数 在什么时候起作用,在我们找到了合适的区间了之后才起作用的,这时候return ,如果还有其他的右区间的话,我们再去找出合适的左右区间,然后再这样弄。等到我们从找到合适区间的地方回溯的时候,我们更新我们已经走过的区间,就是一个点的sum 为左子树和右子树的和,这个只是更新已经走过的区间,没有走过的区间是不会更新下的(与上面的没有优化的区间修改是有差别的,那个是一直找到最后的区间,然后将整棵树都进行权值更新,我举一个例子,我们上面有[1,4]的线段树,我现在要区间修改[1,3]节点上的数据都进行+1操作,我们进行没有优化的区间修改和进行优化的区间修改,我们可以看一下不同;(我都是按照二叉树的格式展示出来,更容易看出来变化),节点数据 为 1 2 3 4。
从这两个区间修改后的线段树来看,我们要修改的区间 为 [1,3] ,我们线段树中已经有了被修改区间完全包围的区间[1,2],所以我们只更新到[1,2]区间这里,我们不在进行下推到[1,1] 和[2,2]了,所以优化版的最底层的[1,1]和[2,2]没有更新,只是将变化值都保存到了lazy 数组中。我们就又到了右子树中([1,3]区间分为[1,2]左子区间和[3,3]右子区间),我们看到在修改[3,3]的时候,我们未优化的与优化的一模一样,因为[3,3]就是最后的节点区间(长度为1),这个就是被修改区间完全包围的区间,因为这里就是最后的节点区间,我们已经不需要进行lazy数组进行保存了,直接进行修改就行了,这个被修改区间包围着才能修改 不懂得,可以看看上面条件和原则,大佬写的很清楚,大家可以看看。左右子树被修改后,我们需要更新我们走过的区间的权值,我们回溯的时候,将权值更新。)。
单点查询
先放出代码:
void ask(int now, int k)
{
if (t[now].l >= t[now].r)
{
cout << t[now].sum << endl;
return;
}
push_down(now, t[now].l, t[now].r);
int mid = (t[now].l + t[now].r) / 2;
if (k <= mid)
ask(now << 1, k);
else
ask(now << 1 | 1, k);
}同样我们也需要push_down 函数,因为可能有区间修改优化版本,所以我们不管是单点查询还是区间查询,我们都要进行push_down 函数进行下推,单点查询其实也是二分+递归,直到我们二分到最后的叶子节点,我们就停止,输出叶子节点的sum,其实与前面的递归与二分基本一样,没有什么两样。就不详细的讲解了。
区间查询
先放出代码:
int query_range(int now, int l, int r)
{
if (t[now].l >= l && t[now].r <= r)
{
return t[now].sum;
}
push_down(now, t[now].l, t[now].r);
int mid = (t[now].l + t[now].r) / 2;
int sum = 0;
if (l <= mid)
sum += query_range(now << 1, l, r);
if (r > mid)
sum += query_range(now << 1 | 1, l, r);
return sum;
}其实,区间查询也是二分+递归。我们一开始区间修改的时候,我们是优化版的区间修改,我们是找区间在修改区间之内的区间,直接使用push_down的,我们就直接修改到了合适区间位置,这个区间下的区间都没有修改权值,所以为我们 lazy数组就在这个合适区间处标记,使得我们知道从这个节点往下的左子树和右子树都没有进行修改权值,使得我们在查询权值的时候,我们可以通过这个lazy 数组,我们就可以修改合适区间下的区间节点了,因为线段树有很多的区间节点,如果我们全部进行更新,但是有的查询点就不在很深的叶子节点上,反而在很浅的层数上,那么我们多进行的递归和二分就很浪费时间。所以我们在区间查询时候,我们也使用这种优化版的写法,二分直到这个区间在查询区间内,我们就直接返回这个大区间的总和;如果我们进行懒惰标记的地方比查询权值的深度浅,我们就会在二分的时候,不断的释放lazy 数组中的变化值,加到下一层的树中,最后直到那个查询范围处。直接return sum 就可以了,使用递归返回sum.
这个是测试代码,里面有前序输出和层次输出的 函数 DFS1,DFS2 ,更能清晰的看出来变化,大家不理解的,可以自己调一下数据,还可以进行VS调试,可以看看每一步在干啥。
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1005;
struct node
{
int l, r; //范围
int left, right; //左右树
int sum;
int lazy;
}t[maxn << 2];
int lazy[maxn << 2];
int a[maxn];
//建立线段树
void build(int now, int l, int r)
{
t[now].l = l;
t[now].r = r;
t[now].left = now << 1;
t[now].right = now << 1 | 1;
if (l >= r)
{
t[now].sum = a[l];
t[now].left = t[now].right = 0;
return;
}
int mid = (l + r) / 2;
build(now << 1, l, mid);
build(now << 1 | 1, mid + 1, r);
t[now].sum = t[now << 1].sum + t[now << 1 | 1].sum;
}
//前序遍历
void dfs(int now)
{
if (t[now].l >= t[now].r)
{
cout << t[now].sum << endl;
return;
}
cout << t[now].sum << endl;
dfs(now << 1);
dfs(now << 1 | 1);
}
//层次遍历
void dfs2(int now)
{
queueq;
q.push(now);
while (!q.empty())
{
int u = q.front();
q.pop();
cout << t[u].sum << ' ';
if (t[u].left)
q.push(t[u].left);
if (t[u].right)
q.push(t[u].right);
}
}
//延迟数组
void push_down(int now, int l, int r)
{
if (lazy[now])
{
int mid = (l + r) / 2;
lazy[now << 1] += lazy[now];
lazy[now << 1 | 1] += lazy[now];
t[now << 1].sum += (mid - l + 1)*lazy[now];
t[now << 1 | 1].sum += (r - mid)*lazy[now];
lazy[now] = 0;
}
}
//单点修改,线段树
void update(int num, int index, int now) //类似于二分查找
{
if (t[now].l >= t[now].r)
{
t[now].sum += num; //可以是替换操作
return;
}
int mid = (t[now].l + t[now].r) / 2; //二分操作
if (index <= mid)
update(num, index, now << 1); //去搜左子树
else
update(num, index, now << 1 | 1); //去搜右子树
t[now].sum = t[now << 1].sum + t[now << 1 | 1].sum; //线段树更新权值
}
//区间修改 有延迟数组 只要区间范围在修改的范围之内,就加到这里,就不在往后再加了。
void update_range(int now, int l, int r, int num)
{
if (l <= t[now].l && r >= t[now].r)
{
lazy[now] += num;
t[now].sum += (t[now].r - t[now].l + 1)*num;
return;
}
//push_down(now, t[now].l, t[now].r);
int mid = (t[now].l + t[now].r) / 2;
if (l <= mid)
update_range(now << 1, l, r, num);
if (r > mid)
update_range(now << 1 | 1, l, r, num);
t[now].sum = t[now << 1].sum + t[now << 1 | 1].sum;
}
//没有延迟数组的区间修改
void update_range2(int now,int l,int r,int num)
{
if(t[now].l>=t[now].r)
{
t[now].sum+=num;
return ;
}
int mid=(t[now].l+t[now].r)/2;
if(l<=mid)
{
update_range2(now<<1,l,r,num);
}
if(mid= t[now].r)
{
cout << t[now].sum << endl;
return;
}
push_down(now, t[now].l, t[now].r);
int mid = (t[now].l + t[now].r) / 2;
if (k <= mid)
ask(now << 1, k);
else
ask(now << 1 | 1, k);
}
//区间查询 延迟数组
int query_range(int now, int l, int r)
{
if (t[now].l >= l && t[now].r <= r)
{
return t[now].sum;
}
push_down(now, t[now].l, t[now].r);
int mid = (t[now].l + t[now].r) / 2;
int sum = 0;
if (l <= mid)
sum += query_range(now << 1, l, r);
if (r > mid)
sum += query_range(now << 1 | 1, l, r);
return sum;
}
int main()
{
memset(lazy, 0, sizeof(lazy));
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
//建树
build(1, 1, n);
//前序遍历 用于测试代码
//dfs(1);
//cout<