【论文笔记】高维基因数据中的特征选择

原论文：Feature Selection for High-Dimensional Genomic Microarray Data

介绍

基因数据通常具有较高的维度，同时可用样本数少。不到100例维度为7000+的带标签的基因表达数据，如何对其建立分类模型？或者如何减少特征维度？

通常，相比对高维数据直接建模，先减少特征维度后建模的方法具有更好的评估表现。

论文提出了使用特征筛选的方法，该特征筛选包含三个阶段：非条件的单因素混合高斯建模，计算信息增益，Markov Blanket筛选。最终筛选出对目标变量有显著影响的特征。

下面将重点介绍这三个处理方法。更多细节可查看原论文。

1. Unconditional Mixture Modeling

首先，假设基因表达量的活动可以看作【off/on】两种状态下的活动。所以基于这个假设，我们可以将基因表达水平想象为一个含有两个分量的高斯混合模型（off状态下的表达水平，on状态下的表达水平）：$P(f_i|{\theta }_i)$，$f_i$表示第$i$基因的表达量，是一个连续型变量，$\theta$表示模型的参数，包括均值，标准差，分量选择的概率分布。

我们可以使用EM算法估计模型参数，得到关于基因表达量的高斯混合模型。

假设上述的高斯混合模型准确地描述了基因表达量的概率分布的话，那么这个模型的贝叶斯误差率则为：

$\frac{1}{N}({\sum }_{j:z_j=0}P(z_j=1|x_j,\theta )+{\sum }_{j:z_j=1}P(z_j=0|x_j,\theta ))$

其中$z_j$表示第$j$个样本的标签或者类别（$z_j\in \{0,1\}$），上式也可以表示如下，原文称其为mixture overlap probability：
$$e=P(z=0)P(d(f_i)=1|z=0)+P(z=1)P(d(f_i)=0|z=1)$$

$P(d(f_i)=1)$表示利用上述的高斯混合模型将基因表达水平为$f_i$的样本判断其类别为1的概率。

注意，得到的每个基因的高斯混合模型可以用来离散化连续变量（计算后验概率$P(z=j|f_i)$，将后验概率最大的$j$值作为新的离散值）。同时，每个基因高斯混合模型的贝叶斯误差率可以用来衡量特征重要性。

2. Information Gain Ranking

信息增益（Information Gain）常用作估计类分布条件概率的方法。假设类标签（假设有 $C$ 个分类）将数据划分为$S_1,...,S_C$ ，特征 $F_i$ 将数据划分为 $E_1,...,E_K$ ，则由于特征 $F_i$ 带来的信息增益为：
$$I_{gain}=H(P(S_1),...,P(S_C))-\sum _{k=1}^{K}P(E_k)H(P(S_1|E_k),...,P(S_C|E_k))$$
使用信息增益可以衡量每个特征对于类标签的重要程度。由此可以得到特征的重要性排序。

3. Markov Blanket Filtering

关于马尔可夫毯，原文给出了如下参考资料：

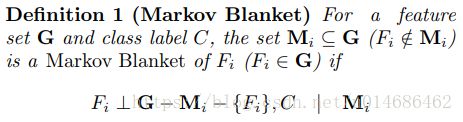
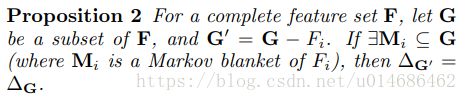
简单来说，某个特征的马尔可夫毯就是一个特征集合，它使得在给定了这个特征集合后，该特征与剩下的所有变量没有任何依赖关系。

也就是说，如果特征 $F_i$ 与其它一些变量集和类标签 $C$ 没有任何依赖关系的话，我们可以移除 $F_i$，这个时候特征 $F_i$ 是存在马尔可夫毯的。

所以，我们可以利用这个性质。马尔可夫毯更进一步证明了使用序列化特征筛选步骤，在这个步骤中，不必要的特征被一步步移除，而这个被移除的特征的马尔可夫毯不需要被知道。

通常情况下，我们寻找近似化的马尔可夫毯，然后计算下式：
$$△(F_i|M)=\sum _{f_M,f_i}P(F=f_i,M=f_M)\cdot D(P(C|F=f_i,M=f_M)||P(C|M=f_M))$$
其中函数$D(P||Q)$ 表示K-L散度。当 $M$ 为特征 $F_i$ 的马尔可夫毯时，$△(F_i|M)=0$。近似化的马尔可夫毯可以使用与$F_i$相关程度（Pearson系数）较高的$k$个特征。具体特征筛选算法伪代码如下：

这种启发式的特征选择方法比其他搜索特征子空间的方法高效得多，只需要计算$P(C|F=f_i,M=f_M),P(C|M=f_M)$。