2019美赛b题:基于Weighted-K-means聚类模型的选址
基于Weighted-K-means聚类模型的选址
(本博客为博主参加2019美赛B题中解决选址问题而使用的算法模型。文字图片皆为原创,引用请注明出处,切勿全篇抄袭。代码已经经过调试,结果正常,如有疑问欢迎留言)
这里贴出题目的要求,感兴趣的同学可以到网上下载2019美赛B题观看
请考虑背景信息,问题陈述中确定的要求以及问题附件中提供的信息,以解决以下问题。
A.为HELP,Inc。DroneGo灾难响应系统推荐无人机机队和一套医疗包,以满足波多黎各飓风情景的要求。为最多三个ISO货物集装箱中的每一个设计相关的包装配置,以将系统运输到波多黎各。
B.确定波多黎各的最佳位置或位置,以定位DroneGo灾难响应系统的一个,两个或三个货物集装箱,以便能够进行医疗供应交付和道路网络的视频侦察。
C.对于DroneGo舰队中包含的每种类型的无人机:
提供无人机有效载荷包装配置(即包装在无人机货舱中的医疗包装),运送路线和时间表,以满足波多黎各飓风情景的已确定的紧急医疗包装要求。提供无人机飞行计划,使DroneGo车队能够使用车载摄像机评估支持Help,Inc。任务的主要高速公路和道路。
工作开始
**说明:在选址模型之前我们小队还自己建了空间分布最优选择模型,主要是通过理论计算,以达到最大服务能力作为出发点,确定工作方案,即将无人机分为两类,一类用于送医疗包,叫做送货无人机(Delivery drone),一类用于拍摄主要道路,叫做航拍无人机(Aerial drone)。 根据医院需求和题目的各种约束,确定送货飞机的类型及数量。
接下来就是第二个棘手的问题啦,选址问题
1、选址数量的确定
(利用最大极限服务范围MLS和波多黎各领土面积PS的比值算出最小ISO数量minNiso,知道了要用三个集装箱)
在上述模型4.1中,我们知道了将无人机分成两类,并算出了完成每个医院送医疗包任务的无人机类型。对于每一套系统,定义了最大极限服务范围MLS来描述它的极限服务范围,考虑无人机往返程,能被表达为:
MLS=pi*(FFD/2)^2
FFD代表无人机最大飞行距离(Farthest flight distance),
参考题目中无人机类型性能,能表达为FFD=MAX(ViFTi)= V2FT2
对于波多黎各,她的地图能近似为一个长方形,其面积可用如下公式表示PS=PL*PW,其中PL,PW分别是波多黎各领土的长和宽,在goolge地图上能得到数值。
因此,最小ISO数量为minNiso=S/MLS=4.192
此数值的得到假设了各个ISO服务范围不重叠情况下,还要再考虑了要给特定位置的医院进行送货,所以此数值还得更大些。
HELP inc最多能给我们提供三个Standard ISO Container Dimensions 用来装包括医疗包、无人机整一套系统,所以我们选用三个ISO,即选出三个地址作为无人机求援系统根据地。minNiso=4.192>3,此不等式也提示着我们这三个系统对于满足整个波多黎各的需求还是不够的,所以我们可以做出些适当的取舍。
2、k-means聚类模型介绍
它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量MC最优分类,使得评价指标D最小。算法采用误差平方和准则函数作为聚类准则函数。最终使得获得的聚类满足同一聚类中的对象相似度较高,聚类中心以及分配给它们的对象就代表一个聚类。核心公式如下:
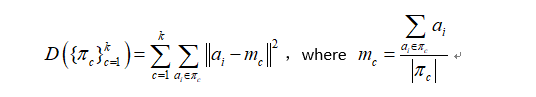
所有元素aij ,i=1,2,…,n. j=1,2…,m. 对于本题m=2,即经度和维度。
k个聚类群组πc, c=1,2,…,k。mc是群组πc内所有元素ai的质心,或叫簇心。程序中不断迭代下去,就能够收敛了,得到最后的聚类效果。
3、 Weighted-K-means聚类模型
为了解决本实际问题,单单使用K-means聚类模型是不够的,因为K-means聚类模型是在对每个散点集的距离比较上都是采用1:1的比例,但是对于我们来说,每个城市的受灾情况和需不需要递送医疗包是不尽相同的,也就是说,簇心到每个散点的路径是加上权重的,所以我们应用了Weighted-K-means聚类模型来解决这个问题。算法核心公式如下:

本公式的计算方法跟k-means算法很相似,只是对于不同的样本点乘多了一个对应的权重wi和权重衰减系数y,当y=0时,Weighted-k-means算法和k-means算法相同,本处取y=1.
算法流程图:
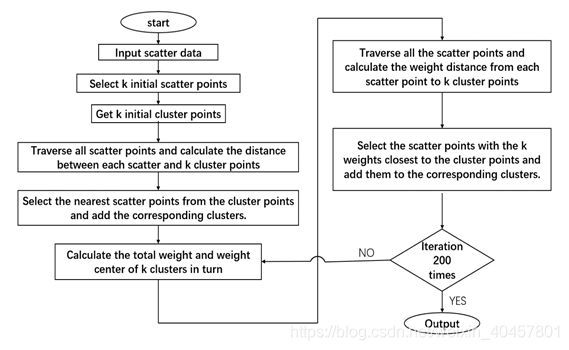
3、1点集的选取
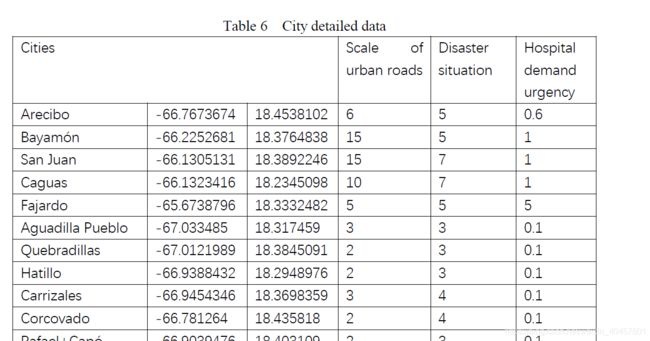
在本题中根据要求,我们知道the DroneGo disaster response system 的位置到各个医院和大部分道路的距离合适,as we know医院在城市当中,城市又通常是道路的交叉节点,所以在聚类模型中散点集直接采用波多黎各的主要城市,一共77个,城市类型用n表示,n=1,2,…,77.。详细数据见附件1。
(当然这里也可以自己选,但一定要保证密度,城市规模都要考虑到,那时我队友还是考虑不是周全的,所以我们用的数据还是有一点点点的问题的)
3、2权值的选取与衡量
(Weighted-K-means模型的灵魂当然是这个Weighted权值的选取啦,参加数学建模的同学肯定知道,解决问题时参数的选取是十分重要的,必须有特殊性、涵盖性)
为了完成题目要求的medical supply delivery and video reconnaissance任务,在选址模型中我们选择权值(w)由三个参数决定:城市道路规模(SURN)、受灾情况(DS)、医院需求紧迫性(HDU)。其中,SURN、DS用来衡量拍摄可行性的估量,HDU用来衡量送医疗包可行性的估量。它们都是可测量的,具体衡量大小的做法见下。对于每个参数各自做归一化处理,对于每个城市,权重表示为:wn=α1SURNn’+α2DSn’+α3*HDUn’. n=1,2,…,77.
为了确定这三个因素中每个部分的权重,我们使用层次分析法(AHP)来确定权重。该方法有助于我们将主观的因素转换为直观的权重,以评估不同因素的重要性。计算过程就不贴出拉,同学们自己百度,这是基础。

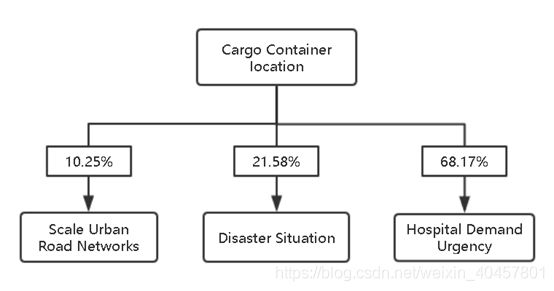
3、3结果作图
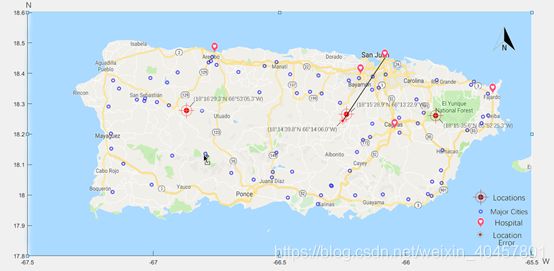
matlab得到经纬度后,采用谷歌地图拟合就得到下图啦,毕竟需要漂亮点
蓝点就是选的 点集,红点为选址点
3、4 matlab实现代码
%%wkm
function [ cluster, cluster_center, cluster_population, cluster_energy, ...
it_num ] = final( dim_num, point_num, cluster_num, it_max, ...
point, weight, cluster, cluster_center )
%%运行时另起m文件,运行函数
%%如[a,b,c,d]=kmeans_w_03 ( 2, 77, 3, 100, cc', w, 1, clusters' )
%%2为维度即经纬度,77为城市数,3为聚类点,100为迭代次数,cc为经纬度数据,w权重数据,由excel导入matlab即可
%%其中cluster为三个聚类点初始点,这里可以自己用matlab随便输入,但要在图中,推荐取 -66 -66 -66;18 18 18
%%1为原先类别,取1就行
%%输出二维数据b即为聚类点经纬度,a为各点的类别123
if ( cluster_num < 1 )
fprintf ( 1, '\n' );
fprintf ( 1, 'KMEANS_W_03 - Fatal error!\n' );
fprintf ( 1, ' CLUSTER_NUM < 1.\n' );
error ( 'KMEANS_W_03 - Fatal error!' )
end
if ( dim_num < 1 )
fprintf ( 1, '\n' );
fprintf ( 1, 'KMEANS_W_03 - Fatal error!\n' );
fprintf ( 1, ' DIM_NUM < 1.\n' );
error ( 'KMEANS_W_03 - Fatal error!' )
end
if ( point_num < 1 )
fprintf ( 1, '\n' );
fprintf ( 1, 'KMEANS_W_03 - Fatal error!\n' );
fprintf ( 1, ' POINT_NUM < 1.\n' );
error ( 'KMEANS_W_03 - Fatal error!' )
end
if ( it_max < 0 )
fprintf ( 1, '\n' );
fprintf ( 1, 'KMEANS_W_03 - Fatal error!\n' );
fprintf ( 1, ' IT_MAX < 0.\n' );
error ( 'KMEANS_W_03 - Fatal error!' )
end
if ( any ( weight(1:point_num) < 0.0 ) )
fprintf ( 1, '\n' );
fprintf ( 1, 'KMEANS_W_03 - Fatal error!\n' );
fprintf ( 1, ' Some weight entry is negative.\n' );
error ( 'KMEANS_W_03 - Fatal error!' )
end
if ( all ( weight(1:point_num) <= 0.0 ) )
fprintf ( 1, '\n' );
fprintf ( 1, 'KMEANS_W_03 - Fatal error!\n' );
fprintf ( 1, ' No weight entry is positive.\n' );
error ( 'KMEANS_W_03 - Fatal error!' )
end
%%%%%%%%%%%%%%%%%%
K=cluster_num;data=point;
sample_num = size(point, 1); % 样本数量 77
sample_dimension = size(point, 2); % 每个样本特征维度 2
clusters = zeros(K, sample_dimension);
minVal = min(data); % 各维度计算最小值
maxVal = max(data); % 各维度计算最大值
for i=1:K
clusters(i, :) = minVal + (maxVal - minVal) * rand();%%clusters是簇点
end
hold on; % 在上次绘图(散点图)基础上,准备下次绘图
% 绘制初始簇心
scatter(clusters(:,1), clusters(:,2), 'red', 'filled'); % 实心圆点,表示簇心初始位置
c = zeros(sample_num, 1); % 每个样本所属簇的编号
PRECISION = 0.001;
iter = 100; % 假定最多迭代100次
% Stochastic Gradient Descendant 随机梯度下降(SGD)的K-means,也就是Competitive Learning版本
basic_eta = 1; % learning rate
for i=1:iter
pre_acc_err = 0; % 上一次迭代中,累计误差
acc_err = 0; % 累计误差
for j=1:sample_num
x_j = data(j, :); % 取得第j个样本数据,这里体现了stochastic性质
% 所有簇心和x计算距离,找到最近的一个(比较簇心到x的模长)
gg = repmat(x_j, K, 1);
gg = gg - clusters;
tt = arrayfun(@(n) norm(gg(n,:)), (1:K)');
[minVal, minIdx] = min(tt);
% 更新簇心:把最近的簇心(winner)向数据x拉动。 eta为学习率.
eta = basic_eta/i;
delta = eta*(x_j-clusters(minIdx,:));
clusters(minIdx,:) = clusters(minIdx,:) + delta;
acc_err = acc_err + norm(delta);
c(j)=minIdx;
end
if(rem(i,10) ~= 0)
continue
end
end
cluster= cluster';
cluster_center=cluster;
for i = 1 : point_num
for j = 1 : cluster_num
cluster_energy(j) = sum ( ...
( point(1:dim_num,i) - cluster_center(1:dim_num,j) ).^2 );
end
[ dummy, cluster(i) ] = min ( cluster_energy(1:cluster_num) );
end
cluster_population(1:cluster_num) = 0;
cluster_weight(1:cluster_num) = 0.0;
for i = 1 : point_num
ci = cluster(i);
cluster_population(ci) = cluster_population(ci) + 1;
cluster_weight(ci) = cluster_weight(ci) + weight(i);
end
cluster_center(1:dim_num,1:cluster_num) = 0.0;
for i = 1 : point_num
j = cluster(i);
cluster_center(1:dim_num,j) = cluster_center(1:dim_num,j) ...
+ weight(i) * point(1:dim_num,i);
end
for i = 1 : cluster_num
if ( 0.0 < cluster_weight(i) )
cluster_center(1:dim_num,i) = cluster_center(1:dim_num,i) ...
/ cluster_weight(i);
end
end
it_num = 0;
distsq = zeros ( cluster_num );
while ( it_num < it_max )
it_num = it_num + 1;
swap = 0;
for i = 1 : point_num
ci = cluster(i);
if ( cluster_population(ci) <= 1 )
continue
end
for cj = 1 : cluster_num
if ( cj == ci )
distsq(cj) = sum ( ...
( point(1:dim_num,i) - cluster_center(1:dim_num,cj) ).^2 ) ...
* cluster_weight(cj) ...
/ ( cluster_weight(cj) - weight(i) );
else if ( cluster_population(cj) == 0 )
cluster_center(1:dim_num,cj) = point(1:dim_num,i);
distsq(cj) = 0.0;
else
distsq(cj) = sum ( ...
( point(1:dim_num,i) - cluster_center(1:dim_num,cj) ).^2 ) ...
* cluster_weight(cj) ...
/ ( cluster_weight(cj) + weight(i) );
end
end
[ dummy, list ] = min ( distsq(1:cluster_num) );
if ( list(1) == ci )
continue
end
cj = list(1);
cluster_center(1:dim_num,ci) = ...
( cluster_weight(ci) * cluster_center(1:dim_num,ci) ...
- weight(i) * point(1:dim_num,i) ) ...
/ ( cluster_weight(ci) - weight(i) );
cluster_center(1:dim_num,cj) = ...
( cluster_weight(cj) * cluster_center(1:dim_num,cj) ...
+ weight(i) * point(1:dim_num,i) ) ...
/ ( cluster_weight(cj) + weight(i) );
cluster_population(ci) = cluster_population(ci) - 1;
cluster_population(cj) = cluster_population(cj) + 1;
cluster_weight(ci) = cluster_weight(ci) - weight(i);
cluster_weight(cj) = cluster_weight(cj) + weight(i);
cluster(i) = cj;
swap = swap + 1;
end
if ( swap == 0 )
break
end
end
cluster_energy(1:cluster_num) = 0.0;
for i = 1 : point_num
ci = cluster(i);
cluster_energy(ci) = cluster_energy(ci) + weight(i) * sum ( ...
( point(1:dim_num,i) - cluster_center(1:dim_num,ci) ).^2 );
end
return
end