算法导论 — 思考题15-3 双调欧几里得旅行商问题

（双调欧几里得旅行商问题）在欧几里得旅行商问题中，给定平面上$n$个点作为输入，希望求出连接所有$n$个点的最短巡游路线。下图(a)给出了一个7点问题的解。此问题是NP难问题，因此大家相信它并不存在多项式时间的求解算法（参见第34章）。
　　J. L. Bentley建议将问题简化，限制巡游路线必须为双调巡游(bitonic tours)，即从最左边的点开始，严格向右前进，直至最右边的点，然后调头严格向左前进，直至回到起始点。下图(b)给出了相同7个点的最短双调巡游路线。问题简化之后，存在一个多项式时间的算法。
　　
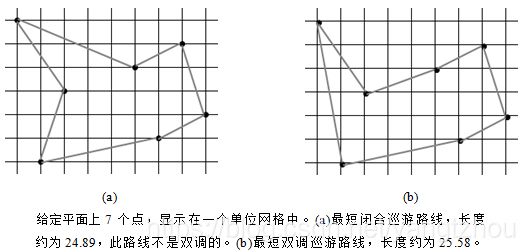
　　设计一个$O(n^2)$时间的最优双调巡游路线算法。你可以认为任何两个点的$x$坐标均不同，且所有实数运算都花费单位时间。（提示：由左至右扫描，对巡游路线的两个部分分别维护可能的最优解。）
　　
　　解
　　对$n$个点按$x$坐标从小到大排序$p_1,p_2,\dots ,p_n$，其中$p_1$为最左边的点，$p_n$为最右边的点。假设$P_{i,j}(i\le j)$表示一条包含$p_1,p_2,\dots ,p_j$的最短双调路径，这条路径从$p_i$向左直到$p_1$，然后从$p_1$向右直到$p_j$。显然，$P_{n,n}$就是本题需要求的路径。假设路径$P_{i,j}$的长度为$l(i,j)$，并且点$p_i$和$p_j$之间的距离为
　　
　　在路径$P_{i,j}$中，$p_i$一定在路径$p_i\to p_1$中，$p_j$一定在路径$p_1\to p_j$中。现在考虑$p_{j-1}$的位置，分以下几种情况：
　　(1) $i<j-1$
　　此时$p_{j-1}$在$p_i$的右边，故$p_{j-1}$只能出现在路径$p_1\to p_j$中。又由于$p_{j-1}$是路径$p_1\to p_j$中除$p_j$外的最右边的点，所以在路径中$p_{j-1}$直接跟$p_j$相连，如下图所示。
　　
　　根据以上分析，当$i<j-1$时，路径$P_{i,j}$的长度等于路径$P_{i,j-1}$的长度加上$||p_{j-1}{p}_j||$。于是可以得到以下递归式
　　
　　(2) $i=j-1$
　　在这种情况下，$p_{j-1}$即是$p_i$，所以$p_{j-1}$一定位于路径$p_i\to p_1$上。而路径$p_1\to p_j$中直接跟$p_j$相连的点可以是$p_1,p_2,\dots ,p_{j-2}$中的任意一点，假设该点为$p_k(1\le k\le j-2)$。如下图所示。
　　
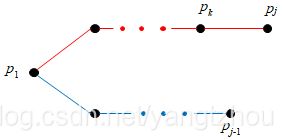
　　路径$P_{i,j}$的长度等于路径$P_{k,j-1}$的长度加上$||p_k{p}_j||$。要使得$P_{i,j}$为最短双调路径，则必须选择合适的$p_k$使得$l(i,j)$最小。于是可以得到以下递归式
　　
　　(3) $i=j$
　　在这种情况下，$P_{i,j}$是一条闭合路径。这种情况只会发生在$i=j=n$，此时的路径为$P_{n,n}$。此时$p_{j-1}$即为$p_{n-1}$，而$p_{n-1}$既可以在$p_n\to p_1$上，也可以在$p_1\to p_n$上。而无论$p_{n-1}$在哪条路径，$p_{n-1}$必然直接连接在$p_n$上，因为$p_{n-1}$是除$p_n$外的最右边的点。如下图所示。
　　
　　路径$P_{n,n}$的长度等于路径$P_{n-1,n}$的长度加上$||p_{n-1}{p}_n||$，即
　　
　　综合上述三种情况，路径$P_{i,j}$的长度满足如下递归式
　　
　　根据以上的递归式，可以使用动态规划方法，按照自底向上的方式计算出最短双调路径$P_{n,n}$的长度$l(n,n)$。
　　然而，我们应当如何得到最短双调路径本身，即路径中所有点的顺序？根据上面的递归过程，每次递归都会找出路径$P_{i,j}$中与最右点$P_j$直接相连的点，可以将这个点保存在数组$left[i,j]$中。从$P_{n,n}$开始，依次找到每条路径的$left[i,j]$即可生成最短双调路径$P_{n,n}$。
　　
　　本节相关的code链接。
　　https://github.com/yangtzhou2012/Introduction_to_Algorithms_3rd/tree/master/Chapter15/Problems/Problem_15-3