Stata: 空间面板数据模型及Stata实现
作者:游万海 (福州大学)
Stata 连享会: 知乎 | 简书 | 码云 | CSDN
本文 PDF 版本 点击下载
![]()
Stata连享会 计量专题 || 精品课程 || 简书推文 || 公众号合集
连享会#金秋十月 @ 空间计量专题 (2019.10.24-27,成都)
![]()
图片来源:Golgher 和 Voss (2016)
1. 背景介绍
由于面板数据模型所具有的众多优点 (刻画个体异质性,减弱模型共线性和增加自由度等),其被广泛应用于实证计量中。在 「 Stata: 面板数据模型-一文读懂」 文中,我们已对面板数据模型进行了介绍。
然而,当研究样本涉及到多个单元时 (如多个国家),研究单元间的空间相关性不可忽略。例如,在利用跨国样本研究环境污染 (如 C O 2 CO_{2} CO2 排放量) 的影响因素时,除考虑该国经济发展水平,人口总数,城市化水平和工业化水平等宏观变量之外,还应将其他研究单元的情况考虑在内,包括他国的环境污染程度 (后文纳入 W Y WY WY 的理论依据) 和宏观经济因素 (后文纳入 W X WX WX 的理论依据)。 理由如下:第一,由于污染的空间流动性,对于一些特定的污染物,本地区的污染水平会对其 “邻近” 地区的污染水平造成影响;第二,当某个地区的经济发展较快时,“邻近” 地区会模仿该地区的经济发展模式和产业布局,进而也会对其环境污染水平造成影响。
正如地理学第一定律 ( Tobler’s First Law ) 所说:任何事物都是与其他事物相关的,只不过相近的事物关联更紧密。空间计量计量学的发展为这一理论研究提供了有力的工具。 本推文将对面板数据框架下的空间计量模型 (空间面板数据模型) 进行讨论。本文主要分四部分内容进行介绍:
- 模型介绍: 空间面板模型简介
- 空间权重矩阵构造
- 模型解释
- 模型实现
2. 模型介绍: 空间面板模型简介
2.1 双向固定效应模型:不考虑空间相关性
在介绍空间面板模型之前,我们先简单回顾一下普通的面板数据模型。这里以双向固定效应模型为例进行说明,详情参见「 Stata: 面板数据模型-一文读懂」 。
面板数据模型同时包含了截面和时间两个维度,后文用 i i i ( i = 1 , ⋯ , N i =1, \cdots, N i=1,⋯,N) 表示截面 (个体), t t t ( t = 1 , ⋯ , T t=1, \cdots, T t=1,⋯,T) 表示时间,设定如下面板数据模型:
y i t = α i + λ t + x i t β + ϵ i t y_{it} = \alpha_{i} + \lambda_{t} + \mathbf{x_{it}}\beta + \epsilon_{it} yit=αi+λt+xitβ+ϵit
其中,
- y i t y_{it} yit 为 N T × 1 NT\times 1 NT×1 因变量,
- x i t \mathbf{x_{it}} xit 为 N T × k NT\times k NT×k 自变量,
- ϵ i t \epsilon_{it} ϵit 为模型误差项, β \beta β是待估计参数,表示 x i t \mathbf{x_{it}} xit对 y i t y_{it} yit 的边际影响。
- α i \alpha_{i} αi 表示个体效应,表示那些不随时间改变的影响因素,如个人的消费习惯、企业文化和经营风格等;
- λ t \lambda_{t} λt 表示时间效应,用于控制随时间改变因素的影响 (时间虚拟变量包括时间趋势项,时间趋势主要用于控制技术进步),如广告的投放 (往往通过电视或广播,我们可以认为在特定的年份所有个体所接受的广告投放量相同)。
显然, α i \alpha_{i} αi 和 λ t \lambda_{t} λt 在多数情况下都是无法直接观测或难以量化的,因此也就无法进入模型。在截面分析中往往会引起遗漏变量的问题。
面板数据模型的主要用途之一就在于处理这些不可观测的个体效应或时间效应。当对所有的 i i i, α i \alpha_{i} αi 均相等时,模型退化为混合数据模型 ( Pooled OLS ),可直接用 reg y x 命令进行参数估计。
2.2 空间面板数据模型
上述模型中解释变量仅仅纳入自身的因素,未考虑其他地区的一些因素。例如,一个国家的 C O 2 CO_{2} CO2 排放水平不仅与其"邻近"地区的 C O 2 CO_{2} CO2 排放水平有关,还可能与其他地区的经济社会等因素存在关联。
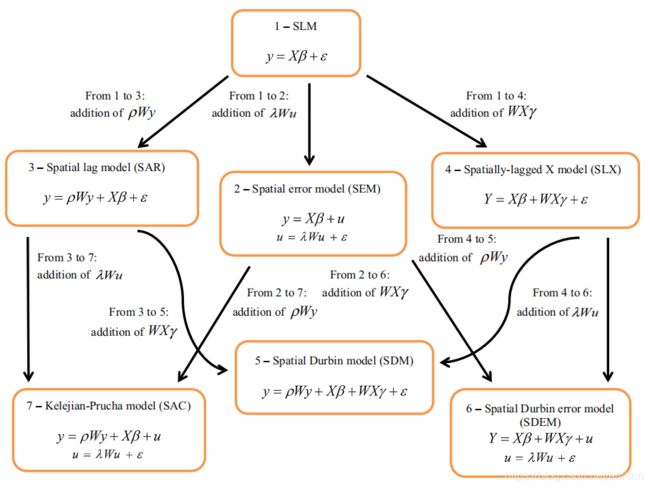
空间面板数据模型进一步加入了空间滞后被解释变量 W Y WY WY 和空间滞后误差项 W ϵ W\epsilon Wϵ。前者称为空间滞后模型,后者称为空间误差模型。两类模型的主要区别在于刻画空间相依方式的不同,前者主要描述空间相依性 ( Spatial dependence ),后者描述空间异质性 ( Spatial heterogeneity )。 进一步地,加入空间滞后解释变量 W X WX WX。考虑到模型的应用广泛性,本推文主要讨论同时纳入 W Y WY WY 和 W X WX WX 的空间模型,该模型称为空间杜宾模型 ( Spatial Durbin model )。模型如下:
y i , t = a i + λ t + ρ ∑ j = 1 N w i , j y i , t + x i , t β + ∑ j = 1 N w i , j x i , j , t θ + ε i t y_{i, t}=a_{i} + \lambda_{t}+\rho \sum_{j=1}^{N} w_{i, j} y_{i, t}+\boldsymbol{x}_{i, t} \boldsymbol{\beta}+\sum_{j=1}^{N} w_{i, j} \boldsymbol{x}_{i, j, t} \boldsymbol{\theta}+\varepsilon_{it} yi,t=ai+λt+ρj=1∑Nwi,jyi,t+xi,tβ+j=1∑Nwi,jxi,j,tθ+εit
进一步,可将该模型写成向量形式:
y t = ρ W y t + x t β + W x t θ + a + λ t ι n + ε t y_{t}=\rho W y_{t}+x_{t} \beta+W x_{t} \theta+a+\lambda_{t} \iota_{n}+\varepsilon_{t} yt=ρWyt+xtβ+Wxtθ+a+λtιn+εt
其中, ε t ∼ N ( 0 , σ ε 2 I n ) \varepsilon_{t} \sim \mathcal{N}\left(0, \sigma_{\varepsilon}^{2} I_{n}\right) εt∼N(0,σε2In) ; a = [ a 1 , a 2 , … , a n ] a=\left[a_{1}, a_{2}, \ldots, a_{n}\right] a=[a1,a2,…,an]; l n l_{n} ln 是 ( n × 1 ) (n \times 1) (n×1) 的列向量,每个元素都为 1。
y t = [ y 1 t y 2 t ⋮ y n t ] , x t = [ 1 x 21 t ⋯ x k 1 t 1 x 22 t ⋯ x k 2 t ⋮ ⋮ ⋱ ⋮ 1 x 2 n t ⋯ x k n t ] y_{t}=\left[ \begin{array}{c}{y_{1 t}} \\ {y_{2 t}} \\ {\vdots} \\ {y_{n t}}\end{array}\right], \ \ x_{t}=\left[ \begin{array}{cccc}{1} & {x_{21 t}} & {\cdots} & {x_{k 1 t}} \\ {1} & {x_{22 t}} & {\cdots} & {x_{k 2 t}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {1} & {x_{2 n t}} & {\cdots} & {x_{k n t}}\end{array}\right] yt=⎣⎢⎢⎢⎡y1ty2t⋮ynt⎦⎥⎥⎥⎤, xt=⎣⎢⎢⎢⎡11⋮1x21tx22t⋮x2nt⋯⋯⋱⋯xk1txk2t⋮xknt⎦⎥⎥⎥⎤
β = [ β 1 , β 2 ⋯ β k ] ′ \beta = \left[ \beta_1, \beta_{2} \cdots \beta_{k} \right]' β=[β1,β2⋯βk]′, θ = [ θ 1 , θ 2 ⋯ θ k ] ′ \theta = \left[ \theta_1, \theta_{2} \cdots \theta_{k} \right]' θ=[θ1,θ2⋯θk]′.
W W W 为空间权重矩阵,其合理定义是应用空间计量模型的一个关键前提。前文我们不厌其烦地多次提到"邻近"地区, W W W 的一个作用就是用于某个地区的"邻近"地区包括哪些。此外,还可通过 W W W 定义邻近地区对本地区的影响方式和程度。
连享会计量方法专题……
3. 空间权重矩阵构造
与普通面板数据模型相比,空间面板数据模型通过引入空间权重矩阵来定义研究单元之间的关联方式和关联程度。从现有文献来看,常用的空间权重矩阵可以归纳为两类。一类为基于地理位置构造的,如 Rook 、 Queen、K-nearest 和 距离倒数次方权重矩阵;一类为基于社会经济因素的空间权重矩阵。前者的优点为直观且满足空间权重矩阵外生性假定,而后者的优点为有较强的经济含义且更符合实际应用背景。基于社会经济因素的空间权重矩阵,由于不同年份的社会经济指标值不同,其通常是随着时间变化而改变,但是此时模型通常较为复杂,实证中常取平均值构造空间权重矩阵 (此外,时变空间权重矩阵也被提出)。
为了对模型进行正确识别,必须保证空间权重矩阵的外生性。基于经济社会因素构造的空间权重矩阵有时经济含义较为明显,但是通常都不满足外生性假设。因此,在实际应用中最常用的空间权重矩阵是基于地理信息或者地理位置的,如 Rook,Queen 以及距离权重矩阵。
3.1 Rook 和 Queen 权重矩阵
例如,在省域环境问题研究中,通常认为"邻近"省份的环境治理行为存在相似。这里的"邻近"可以认为从地理位置来看,两个省份存在地理接壤。若存在共同边界,元素设定为 1,否则设定为 0。假设我们有 5 个省份 (下文统称为 单元#),其地理分布如下图所示
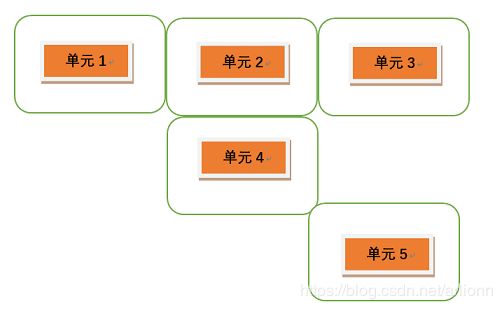
则 Rook 空间权重矩阵是一个 5 行 5 列的方阵:
W R o o k = ( 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 ) 5 × 5 W_{Rook} = \left( \begin{array}{ccc}{0} & {1} & {0} & {0} & {0} \\ {1} & {0} & {1} & {1} & {0} \\ {0} & {1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {0} \end{array}\right)_{5\times 5} WRook=⎝⎜⎜⎜⎜⎛0100010110010000100000000⎠⎟⎟⎟⎟⎞5×5
具体解释如下:
- W R o o k W_{Rook} WRook 矩阵的对角线元素均为 0。这很显然。否则的话,你怎么解释 “我自己和自己相邻” 呢?
- W R o o k W_{Rook} WRook 矩阵的第一行表示 单元1 与各个单元之间的相邻关系。以第一行第二列为例, W R o o k [ 1 , 2 ] = 1 W_{Rook}[1,\ 2] = 1 WRook[1, 2]=1,表示 单元1 与 单元2 相邻。按此逻辑,我们很容易猜知 W R o o k [ 2 , 1 ] = 1 W_{Rook}[2,\ 1] = 1 WRook[2, 1]=1。
- 细心的读者可以看出,在上例中,单元5 与其他单元都不存在共同边界,导致 W R o o k W_{Rook} WRook 矩阵的第 5 行元素的值全部为 0。例如,在我国省域单元研究中,海南省就是这样的情况。Rook 空间权重矩阵的设定不允许出现这种情况。因此,在实际分析中,若利用 Rook 空间权重矩阵,通常假设海南省与广东省存在相邻。
对于这种 孤零零的单元,另一种处理办法是放宽假设,可以认为只要存在顶点相接,就认为两地区为"邻居"关系,这就是 Queen 空间权重矩阵。按照这一设定,空间权重矩阵可定义为
W Q u e e n = ( 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 0 1 0 ) W_{Queen} = \left( \begin{array}{ccc}{0} & {1} & {0} & {0} & {0} \\ {1} & {0} & {1} & {1} & {0} \\ {0} & {1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} & {1} \\ {0} & {0} & {0} & {1} & {0} \end{array}\right) WQueen=⎝⎜⎜⎜⎜⎛0100010110010000100100010⎠⎟⎟⎟⎟⎞
3.2 距离权重矩阵
前文已经提及,空间权重矩阵不仅可以定义 关联方式 (是否关联),而且可以定义 关联程度 (关联的紧密程度)。然而基于 Rook 和 Queen 的空间权重矩阵假定两个地区只要存在关联,其关联程度都是相同的 (等权重)。然而,这种假定往往有悖常理。例如,在环境污染研究中,一般认为距离近的地区,关联程度较高;又如,在国际贸易研究中,往来密切的地区之间关联程度较高。在这种情况下,基于空间距离的权重矩阵较为合适。基于距离的空间权重矩阵定义如下:
w i j = 1 / d i j 2 d i j = arcos [ ( sin ϕ i × sin ϕ j ) + ( cos ϕ i × cos ϕ j × cos ( Δ τ ) ) ] × R \begin{array}{c}{w_{i j}=1 / d_{i j}^{2}} \\ {d_{i j}=\operatorname{arcos}\left[\left(\sin \phi_{i} \times \sin \phi_{j}\right)+\left(\cos \phi_{i} \times \cos \phi_{j} \times \cos (\Delta \tau)\right)\right] \times R}\end{array} wij=1/dij2dij=arcos[(sinϕi×sinϕj)+(cosϕi×cosϕj×cos(Δτ))]×R
其中: ϕ i \phi_{i} ϕi 和 ϕ j \phi_{j} ϕj分别表示某个国家 (如最大城市或首都) 的纬度和经度; Δ τ \Delta \tau Δτ为两个国家间经度之差; R R R为地球半径,等于 3958.761英里。在实际应用中,常对空间权重矩阵进行行标准化,空间权重矩阵的对角元素设为 0。
3.3 经济权重矩阵
与基于地理信息构造的空间权重矩阵相比,经济权重矩阵的实际应用背景较强,其没有统一的数学表达式。例如,研究经济增长影响因素时,研究样本为世界各国,一般认为两国间的贸易往来越多,它们之间的经济增长水平联系越紧密,此时可根据两国的贸易往来数据构造空间权重矩阵,空间权重矩阵定义如下:
w i j = 1 2 T ∑ t ∈ T ( e x p o r t i j , t ∑ j e x p o r t i j , t + i m p o r t i j , t ∑ j i m p o r t i j , t ) w_{i j}=\frac{1}{2 T} \sum_{t \in T}\left(\frac{e x p o r t_{i j, t}}{\sum_{j} e x p o r t_{i j, t}}+\frac{i m p o r t_{i j, t}}{\sum_{j} i m p o r t_{i j, t}}\right) wij=2T1t∈T∑(∑jexportij,texportij,t+∑jimportij,timportij,t)
其中: e x p o r t i j , t export_{ij,t} exportij,t表示在时刻 t t t国家 i i i向国家 j j j的出口总量, i m p o r t i j , t import_{ij,t} importij,t表示在时刻 t t t国家 i i i向国家 j j j的进口总量, T T T为时间长度。该式表示两国间的相似度为时间 T T T内双边贸易的平均。
再如,基于 GDP 的空间权重可以定义为
w i j = 1 − ∣ ( G D P j − G D P i ) / ( G D P j + G D P i ) ∣ w_{i j}=1-|\left(G D P_{j}-G D P_{i}\right) /\left(G D P_{j}+G D P_{i}\right)| wij=1−∣(GDPj−GDPi)/(GDPj+GDPi)∣
其中, G D P i GDP_{i} GDPi 和 G D P j GDP_{j} GDPj 分别表示研究时间内国家 i i i 和国家 j j j GDP 平均值, w i j w_{i j} wij 的取值范围为 0-1,可以看出,当两国的 GDP 较为接近时, w i j w_{i j} wij=1,当两国的 GDP 差异非常显著时, w i j = 0 w_{i j}=0 wij=0。值得注意的是,该空间权重矩阵并不随时间在改变。若针对不同时间 t t t,将 w i j , t w_{ij,t} wij,t 值设定为不同的数值,此时的空间权重矩阵为时变的,对于该类模型的研究,详细可以参考 Lee and Yu (2012)。
连享会计量方法专题……
4. 模型解释
4.1 非空间面板数据模型
当假设研究单元不相依时 (independence),在时刻 t t t, 对所有的 i i i,有
∂ E ( y i ) / ∂ x i = β ∂ E ( y i ) / ∂ x j = 0 , i ≠ j \begin{array}{l}{\partial E\left(y_{i}\right) / \partial x_{i}=\beta} \\ {\partial E\left(y_{i}\right) / \partial x_{j}=0, i \neq j}\end{array} ∂E(yi)/∂xi=β∂E(yi)/∂xj=0,i̸=j
根据上述式子可知,模型系数和边际效应大小相同,解释变量 X 1 X_{1} X1 对 Y Y Y 的影响作用大小可以根据模型系数进行解释。
4.2 空间面板数据模型
空间计量模型因为包含 W y t W y_{t} Wyt 和 W x t W x_{t} Wxt ,某个解释变量对被解释变量的总效应与其系数大小并不相等,此时总效应包括两部分:自身 (own-region) 的直接效应和其他单元引起的间接效应 (又称空间溢出效应, spatial spillover )。
也就是说,某一单元 i i i 在时刻 t t t 的解释变量 x x x 的变动不仅会对该单元 (即 i i i ) 自身的被解释变量有直接影响,也会对其他单元 (即 单元 i i i 的 “邻居”) 的被解释变量有间接影响并最终会反过来影响单元 i i i (因为对于其他单元, i i i 也是其 “邻居”),这与非空间面板数据模型存在明显的不同。
4.3 直接效应,间接效应和总效应
为了解决空间计量模型系数难以解释问题,LeSage 和 Pace (2009) 提出直接效应 (direct effects, DE), 间接效应 (indirect effects, IE) 和 总效应 (total effects, TE)。对于空间 Durbin 模型,模型可以表示为
y t = ( I − ρ W ) − 1 ( α + x t β + W x t θ + λ t ι n + ε t ) E ( y t ∣ x t ) = ( I − ρ W ) − 1 ( α + x t β + W x t θ + λ t ι n ) \begin{aligned} y_{t} &=(I-\rho W)^{-1}\left(\alpha+x_{t} \beta+W x_{t} \theta+\lambda_{t} \iota_{n}+\varepsilon_{t}\right) \\ E\left(y_{t} | x_{t}\right) &=(I-\rho W)^{-1}\left(\alpha+x_{t} \beta+W x_{t} \theta+\lambda_{t} \iota_{n}\right) \end{aligned} ytE(yt∣xt)=(I−ρW)−1(α+xtβ+Wxtθ+λtιn+εt)=(I−ρW)−1(α+xtβ+Wxtθ+λtιn)
其中,在特定稳定条件下, ( I − ρ W ) − 1 = I + ρ W + ρ 2 W 2 + ρ 3 W 3 + … \left(\mathbf{I}-\rho \mathbf{W}\right)^{-1}=\mathbf{I}+\rho \mathbf{W}+\rho^{2} \mathbf{W}^{2}+\rho^{3} \mathbf{W}^{3}+\ldots (I−ρW)−1=I+ρW+ρ2W2+ρ3W3+…
为了更为直观理解上述公式,以下用截面数据框架下 SAR 模型 (仅考虑 W Y WY WY) 为例,有
E ( y ∣ X ) = ( I − ρ W ) − 1 X β E(\mathbf{y} | \mathbf{X})=(\mathbf{I}-\rho \mathbf{W})^{-1} \mathbf{X} \beta E(y∣X)=(I−ρW)−1Xβ
若研究样本为中国 34 个省级行政区域,经济发展水平为解释变量,记为 X 0 X_{0} X0,环境污染水平为被解释变量,记为 y y y。保持 X 0 X_{0} X0 的其他值不变,将福建省所对应的样本观察值修改为某个数值,将修改后变量记为 X 1 X_{1} X1, 则有
E ( y ∣ X 1 ) − E ( y ∣ X 0 ) = ( I − ρ W ) − 1 X 1 β − ( I − ρ W ) − 1 X 0 β = ( I − ρ W ) − 1 Δ X β = ( I + ρ W + ρ 2 W 2 + ρ 3 W 3 + … ) Δ X β = Δ X β + ρ W Δ X β + ρ 2 W 2 Δ X β + ρ 3 W 3 Δ X β + … \begin{array}{l}{E\left(\mathbf{y} | \mathbf{X}_{1}\right)-E\left(\mathbf{y} | \mathbf{X}_{0}\right)} \\ {=(\mathbf{I}-\rho \mathbf{W})^{-1} \mathbf{X}_{1} \beta-(\mathbf{I}-\rho \mathbf{W})^{-1} \mathbf{X}_{0} \beta} \\ {=(\mathbf{I}-\rho \mathbf{W})^{-1} \Delta \mathbf{X} \beta}\\{=\left(\mathbf{I}+\rho \mathbf{W}+\rho^{2} \mathbf{W}^{2}+\rho^{3} \mathbf{W}^{3}+\ldots\right) \Delta \mathbf{X} \beta}\\{=\Delta \mathbf{X} \beta+\rho \mathbf{W} \Delta \mathbf{X} \beta+\rho^{2} \mathbf{W}^{2} \Delta \mathbf{X} \beta+\rho^{3} \mathbf{W}^{3} \Delta \mathbf{X} \beta+\ldots} \end{array} E(y∣X1)−E(y∣X0)=(I−ρW)−1X1β−(I−ρW)−1X0β=(I−ρW)−1ΔXβ=(I+ρW+ρ2W2+ρ3W3+…)ΔXβ=ΔXβ+ρWΔXβ+ρ2W2ΔXβ+ρ3W3ΔXβ+…
[ ∂ E ( y 1 ) ∂ x 1 ⋯ ∂ E ( y 1 ) ∂ x n ⋮ ⋱ ⋮ ∂ E ( y n ) ∂ x 1 ⋯ ∂ E ( y n ) ∂ x n ] = ( I − ρ W ) − 1 [ β k w 12 θ k ⋯ w 1 n θ k w 21 θ k β k ⋯ w 2 n θ k ⋮ ⋮ ⋱ ⋮ w n 1 θ k w n 2 θ k ⋯ β k ] \left[ \begin{array}{cccccc}{\frac{\partial E\left(y_{1}\right)}{\partial x_{1}}} & {\cdots} & {\frac{\partial E\left(y_{1}\right)}{\partial x_{n}}} \\ {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial E\left(y_{n}\right)}{\partial x_{1}}} & {\cdots} & {\frac{\partial E\left(y_{n}\right)}{\partial x_{n}}}\end{array}\right]=(\mathbf{I}-\rho \mathbf{W})^{-1} \left[ \begin{array}{cccc}{\beta_{k}} & {w_{12} \theta_{k}} & {\cdots} & {w_{1 n} \theta_{k}} \\ {w_{21} \theta_{k}} & {\beta_{k}} & {\cdots} & {w_{2 n} \theta_{k}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {w_{n 1} \theta_{k}} & {w_{n 2} \theta_{k}} & {\cdots} & {\beta_{k}}\end{array}\right] ⎣⎢⎢⎡∂x1∂E(y1)⋮∂x1∂E(yn)⋯⋱⋯∂xn∂E(y1)⋮∂xn∂E(yn)⎦⎥⎥⎤=(I−ρW)−1⎣⎢⎢⎢⎡βkw21θk⋮wn1θkw12θkβk⋮wn2θk⋯⋯⋱⋯w1nθkw2nθk⋮βk⎦⎥⎥⎥⎤
= { ( I − ρ W ) − 1 × ( β k I + θ k W ) } =\left\{(\mathbf{I}-\rho \mathbf{W})^{-1} \times\left(\beta_{k} \mathbf{I}+\theta_{k} \mathbf{W}\right)\right\} ={(I−ρW)−1×(βkI+θkW)}
4.3.1 直接效应
直接效应为上述矩阵对角元素的平均值,若 A d ‾ A^{\overline{d}} Ad 表示对矩阵 A A A 的对角线元素求行平均,此时 DE 可以表示为:
D E = { ( I − ρ W ) − 1 × ( β k I + θ k W ) } d ‾ DE = \left\{(\mathbf{I}-\rho \mathbf{W})^{-1} \times\left(\beta_{k} \mathbf{I}+\theta_{k} \mathbf{W}\right)\right\}^ {\overline{d}} DE={(I−ρW)−1×(βkI+θkW)}d
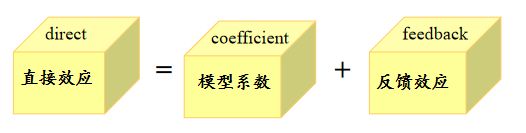
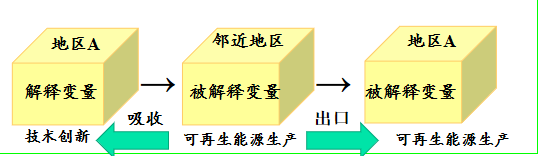
直接效应 表示的是某地区自变量对该因变量的影响大小,其包括反馈效应 (feedback effects, FE),即对其他地区的影响又会反过来影响该地区。从数值上来看,直接效应等于空间 Durbin 模型系数与反馈效应之和。具体地,反馈效应 指的是某个地区的解释变量 (如:技术创新) 会对其"邻近"地区的被解释变量 (如:可再生能源生产量),反过来又会影响该地区的被解释变量 (如:可再生能源生产量)。例如:某地区技术会被其"邻近"地区模仿与采用,用来生产可再生能源,这些地区又可将生产的再生能源出口到本地区,进而影响本地区的可再生能源量。
4.3.2 间接效应
间接效应 为矩阵非对角元素的行平均,若 A r s u m ‾ A^{\overline{\mathrm{rsum}}} Arsum 表示对矩阵 A A A 的非对角线元素求行平均,即 IE 可以表示为:
I E = { ( I − ρ W ) − 1 × ( β k I + θ k W ) } r s u m ‾ IE = \left\{(\mathbf{I}-\rho \mathbf{W})^{-1} \times\left(\beta_{k} \mathbf{I}+\theta_{k} \mathbf{W}\right)\right\}^ {\overline{\mathrm{rsum}}} IE={(I−ρW)−1×(βkI+θkW)}rsum
间接效应,又称为空间溢出效应 (spatial spillover effects),用于度量“邻近”地区的某个解释变量(如:技术创新)对本地区的被解释变量的影响 (如:可再生能源生产)。值得注意的是,不能仅仅依靠空间自回归系数 ρ \rho ρ显著与否来判断空间效应的存在。
4.3.3 总效应
总效应为直接效应和间接效应之和,即 T E = D E + I E TE = DE + IE TE=DE+IE。其可以解释为某一地区的某个解释变量的变动对所有地区的被解释变量的平均影响。本部分主要讨论空间杜宾模型下的直接效应,间接效应(空间溢出效应)和总效应的计算,其他模型形式可以参考 LeSage和Pace(2009)。
5. 模型实现
5.1 命令语法介绍
空间面板数据模型中包括了 W y Wy Wy,该变量为内生变量。相比静态面板数据模型,其估计更为复杂。当前常用的方法包括三种,包括:广义矩估计法 (GMM)、极大似然估计法 (ML) 和贝叶 斯 MCMC 估计法。GMM 估计的思路是将模型作为普通的动态面板数据模型进行估计,这时候 w y i , t wy_{i,t} wyi,t 存在内生性,应该设定相应的工具变量。具体地,可先利用 splagvar 或者 spgenerate 命令生成变量 w ∗ y i , t w*y_{i,t} w∗yi,t,进而利用 xtabond2 命令进行动态面板数据模型估计。在贝叶斯估计方法,更加详细可以参考 LeSage和Pace (2009)。本部分所介绍的 Stata 命令,主要是基于极大似然法进行参数估计。
Stata 15 版增加相应的空间计量模型估计 (help spxtregress)和相关检验命令 (help spxtregress postestimation),在估计模型后可以通过 estat impact 计算直接效应,间接效应和总效应。详细的手册可以参考「 Stata: Stata 15 PDF 电子手册」 。目前,spxtregress 还不支持动态空间面板数据模型估计,这里主要介绍 Federico Belotti等人开发的 xsmle 命令,该命令同时支持空间动态面板数据模型的估计,该命令已发表在 Stata Journal,更为详细的可以参见
「 Spatial panel-data models using Stata 」。
以空间杜宾模型为例, xsmle 语法如下:
xsmle depvar [indepvars] [if] [in] [weight] , ///
wmat(name) model(sdm) [SDM_options]
为了方便说明,同时列出普通面板数据模型的命令语法,
xtreg depvar [indepvars] [if] [in] [weight] , fe [FE_options]
对比可以发现,xsmle 命令增加了 wmat() 和 model() 这两个选项。model() 用于定义空间面板数据模型形式,包括空间杜宾模型 (SDM),空间滞后模型 (Spatial Autoregressive model, SAR),空间误差模型 (Spatial Error model, SEM),空间自相关模型 (Spatial Autocorrelation model, SAC),以及广义空间面板随机效应模型(Generalized Spatial Panel Random Effects model, GSRE)。
连享会计量方法专题……
5.2 空间权重矩阵生成
前文已经介绍,利用空间计量模型的一个重要前提是空间权重矩阵的合理定义,wmat 选项就是用于空间权重矩阵,其可以为 Stata 中矩阵或者 spmat 目标(即利用 spmat 产生, help spmat )。下文基于地理位置信息构造空间权重矩阵进行说明。
为了计算该类空间权重矩阵,首先需要获得研究单元的地理位置信息,如经度和维度。当研究样本为国家时,通常以国家的首都或者最大城市位置信息作为国家位置的代表。获取经度和维度有多种途径,比较方便的是下载到研究单元对象的 ESRI Shapefile (shapefile) 文件。中国的 shape 文件,包括省级,市级和县级的可以在国家基础信息中心申请下载 (各大论坛应该也有)。若研究的样本为世界各个国家,可以到 (http://www.diva-gis.org/gdata) 下载 。 例如,下载的 shape 文件包括:
- TM_WORLD_BORDERS_SIMPL-0.2.dbf
- TM_WORLD_BORDERS_SIMPL-0.2.shp
- TM_WORLD_BORDERS_SIMPL-0.2.shx
- TM_WORLD_BORDERS_SIMPL-0.2.prj
首先,生成样本数据,这里假设研究样本为 10 个国家,时间为 1935 到 1954 年。
clear
input str16 countries
"China"
"United States"
"Germany"
"Japan"
"India"
"Brazil"
"Russia"
"South Africa"
"United Kingdom"
"Spain"
end
expand 20
sort countries
bys countries:gen year = _n + 1934
egen company = group(countries)
merge 1:1 company year using grunfeld
keep if _merge==3
drop _merge time
save G:\sample_sp,replace
若以 invest 为因变量,mvalue 和 kstock 为自变量。若采用普通面板固定效应模型,在声明面板数据结构后,可利用如下命令进行估计:
xtreg invest mvalue kstock,fe
若采用空间面板数据模型进行建模,则还需要找出这些国家的经度和维度等地理信息。前文已经说明了如何下载 shapefile 文件,该文件中即包含了各个国家的地理信息。那么可以将研究单元数据和 shapefile 进行合并。这里需要用到 shp2dta 命令读取 shapefile 文件,该命令为外部命令,安装方式参考「 Stata: 外部命令的搜索、安装与使用」 。
. cd "c:\"
. shp2dta using "TM_WORLD_BORDERS_SIMPL-0.2.shp", ///
database(data_db) coordinates(data_xy) ///
genid(id) gencentroids(c) replace
. use "data_db", clear
. rename NAME countries
. list countries LAT LON in 1/10
+-----------------------------------------+
| countries LAT LON |
|-----------------------------------------|
1. | Antigua and Barbuda 17.078 -61.783 |
2. | Algeria 28.163 2.632 |
3. | Azerbaijan 40.43 47.395 |
4. | Albania 41.143 20.068 |
5. | Armenia 40.534 44.563 |
|-----------------------------------------|
6. | Angola -12.296 17.544 |
7. | American Samoa -14.318 -170.73 |
8. | Argentina -35.377 -65.167 |
9. | Australia -24.973 136.189 |
10. | Bahrain 26.019 50.562 |
+-----------------------------------------+
读取 shapefile 后,可以发现有 LAT 和 LON 两个变量,分别代表了对应国家的纬度和经度。
接下来,利用该数据和样本数据 sample_sp.dta 根据 countries 这一变量进行合并,并将数据保存为 spatial_weight.dta。
merge 1:m countries using "G:\sample_sp.dta"
keep if _merge==3
drop _merge
keep countries year LAT LON invest mvalue kstock
sort countries year
by countries, sort: list, constant
bys countries: keep if _n==1
save G:\spatial_weight.dta,replace
为了构造空间权重矩阵,利用上述生成的 spatial_weight.dta 数据中的纬度和经度信息进行计算。这里可以利用 spwmatrix生成空间权重矩阵。该命令可以构造多种形式的空间权重矩阵,包括基于地理位置信息的距离权重矩阵,基于经济社会变量的经济权重矩阵。此外,也可以导入 Geoda 生成的 gal 文件,或直接导入 txt 文件。
例如,可利用上面代码产生距离倒数空间权重矩阵
use "G:\spatial_weight.dta",clear
spwmatrix gecon LAT LON, wn(example_w2) ///
wtype(inv) r(3958.761) alpha(1) ///
xport(example_w2,txt) row replace
spmat import example_w2 using example_w2.txt,replace
spmat save example_w2 using example_w2m.spmat,replace
spmat use WW using example_w2m.spmat,replace
我们来看 spwmatrix 命令的语法:
spwmatrix gecon varlist [if] [in], ///
wname(wght_name) ///
[wtype(bin|inv|econ|invecon) ///
cart r(#) dband(numlist) ///
alpha(#) knn(#) ///
econvar(varname1) beta(#) Other_options]
wname() 填写生成的矩阵名称,wtype() 内填写生成矩阵类型,如 bin 表示 binary 二元权重矩阵,inv 表示生成逆距离矩阵,econ 为经济权重矩阵等。r() 内填写地球半径,单位可以是英里或者千米。alpha() 内填写数字,如 1 表示距离 1 次方倒数,2 表示距离平方的倒数。knn() 用于定义最邻近单元个数。row 表示对该矩阵进行行标准化。
在运行 spwmatrix 后,在本地会生成 example_w2.txt 文件,可以将其导入到 Stata 中查看,
insheet using "example_w2.txt", clear delimiter(" ") names
drop v1
rename (v#) (v#),renumber
export excel using "spatial_weight.xls",replace
list in 1/10
上述生成的 spatial_weight.xls文件就可以导入到 R 或 Matlab 中运行。
此外,也可以生成 k-nearest 空间权重矩阵,代码如下:
use G:\spatial_weight.dta,clear
spwmatrix gecon LAT LON, ///
wn(knear_w) knn(5) ///
xport(distant_nearest,txt) ///
row replace /*这里定义最近的5个地区为邻居*/
spmat import nearest_w using distant_nearest.txt,replace
spmat save nearest_w using nearest_w.spmat,replace
spmat use WW using nearest_w.spmat,replace
5.3 空间面板数据模型估计
根据步骤 (2) ,我们已经生成了空间权重矩阵,接下来按照第 (1) 部分生成的 sample_sp.dta 数据进行实证建模
cd "H:\"
use spatial_weight.dta,clear
spwmatrix gecon LAT LON, ///
wn(example_w2) wtype(inv) ///
r(3958.761) alpha(1) ///
xport(example_w2,txt) row replace
spmat import example_w2 using "example_w2.txt", replace
spmat save example_w2 using "example_w2m.spmat", replace
spmat use WW using "example_w2m.spmat", replace
use sample_sp.dta,clear
rename company id
xtset id year,y
local xorg "invest mvalue kstock"
foreach f of local xorg {
gen ln`f' = log(`f')
}
est clear
eststo: xtreg lninvest lnmvalue lnkstock, fe /*普通面板数据模型*/
eststo:xsmle lninvest lnmvalue lnkstock, fe ///
model(sar) wmat(WW) type(both) ///
effects nolog /*空间面板数据模型:SAR model*/
估计结果显示如下:
convergence not achieved
Computing marginal effects standard errors using MC simulation...
SAR with spatial and time fixed-effects Number of obs = 200
Group variable: id Number of groups = 10
Time variable: year Panel length = 20
R-sq: within = 0.4258
between = 0.8555
overall = 0.8165
Mean of fixed-effects = 3.5886
Log-likelihood = 31.1740
------------------------------------------------------------------------------
lninvest | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Main |
lnmvalue | .3087483 .0771167 4.00 0.000 .1576024 .4598942
lnkstock | .0788984 .0306623 2.57 0.010 .0188015 .1389953
-------------+----------------------------------------------------------------
Spatial |
rho | -.4325611 .167113 -2.59 0.010 -.7600965 -.1050257
-------------+----------------------------------------------------------------
Variance |
sigma2_e | .0415918 .0042036 9.89 0.000 .0333528 .0498308
-------------+----------------------------------------------------------------
LR_Direct |
lnmvalue | .3189515 .0808705 3.94 0.000 .1604482 .4774549
lnkstock | .079349 .0306296 2.59 0.010 .019316 .1393819
-------------+----------------------------------------------------------------
LR_Indirect |
lnmvalue | -.0952446 .0387047 -2.46 0.014 -.1711044 -.0193847
lnkstock | -.0239403 .0128027 -1.87 0.061 -.0490331 .0011526
-------------+----------------------------------------------------------------
LR_Total |
lnmvalue | .223707 .064382 3.47 0.001 .0975205 .3498934
lnkstock | .0554087 .0221398 2.50 0.012 .0120155 .098802
------------------------------------------------------------------------------
从结果来看,出现了 convergence not achieved,表明在规定迭代次数内,模型未收敛。这时候可以通过 copy() 选项进行调整,大致的思路是先根据现有估计结果,将模型参数估计系数作为初始值进行迭代。代码如下:
eststo:xsmle lninvest lnmvalue lnkstock, ///
fe model(sar) wmat(WW) type(both) effects nolog ///
from(0.308 0.078 0.5 0.0418,copy)
结果显示如下:
Computing marginal effects standard errors using MC simulation...
SAR with spatial and time fixed-effects Number of obs = 200
Group variable: id Number of groups = 10
Time variable: year Panel length = 20
R-sq: within = 0.4213
between = 0.8549
overall = 0.8155
Mean of fixed-effects = 3.6617
Log-likelihood = 31.1653
------------------------------------------------------------------------------
lninvest | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Main |
lnmvalue | .3079884 .0772697 3.99 0.000 .1565426 .4594342
lnkstock | .0789791 .0307231 2.57 0.010 .0187628 .1391954
-------------+----------------------------------------------------------------
Spatial |
rho | -.4491497 .1674137 -2.68 0.007 -.7772745 -.1210249
-------------+----------------------------------------------------------------
Variance |
sigma2_e | .0417572 .0042414 9.85 0.000 .0334441 .0500703
-------------+----------------------------------------------------------------
LR_Direct |
lnmvalue | .3186822 .0811596 3.93 0.000 .1596123 .4777522
lnkstock | .079556 .0307443 2.59 0.010 .0192983 .1398136
-------------+----------------------------------------------------------------
LR_Indirect |
lnmvalue | -.0981599 .03883 -2.53 0.011 -.1742652 -.0220546
lnkstock | -.0247473 .0129782 -1.91 0.057 -.0501842 .0006895
-------------+----------------------------------------------------------------
LR_Total |
lnmvalue | .2205223 .0635574 3.47 0.001 .0959521 .3450926
lnkstock | .0548086 .0218984 2.50 0.012 .0118885 .0977288
------------------------------------------------------------------------------
(est20 stored)
可以发现,在调整初始值后,模型达到收敛 ( convergence )。在这里需要特别强调,有时候估计模型时也会出现 initial values not feasible ,这时候必须通过**copy()**选项进行设置调整。
现在我们来看下结果,Main 为模型估计系数 β \beta β,rho 为模型中空间自相关系数的 ρ \rho ρ,LR_Direct 为直接效应,LR_indirect 为间接效应,LR_Total 为总效应,即直接效应和间接效应之和。
接下来,将 model(sar) 中修改为 sdm,即估计空间杜宾模型,结果如下:
eststo:xsmle lninvest lnmvalue lnkstock, fe ///
model(sdm) wmat(WW) type(both) effects nolog
Warning: All regressors will be spatially lagged
**convergence not achieved**
Computing marginal effects standard errors using MC simulation...
SDM with spatial and time fixed-effects Number of obs = 200
Group variable: id Number of groups = 10
Time variable: year Panel length = 20
R-sq: within = 0.6420
between = 0.8481
overall = 0.6868
Mean of fixed-effects = -3.0978
Log-likelihood = 34.2413
------------------------------------------------------------------------------
lninvest | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Main |
lnmvalue | .3992177 .0907614 4.40 0.000 .2213286 .5771068
lnkstock | .1580089 .0429793 3.68 0.000 .073771 .2422469
-------------+----------------------------------------------------------------
Wx |
lnmvalue | .60829 .3927921 1.55 0.121 -.1615683 1.378148
lnkstock | .5086279 .209802 2.42 0.015 .0974236 .9198323
-------------+----------------------------------------------------------------
Spatial |
rho | -.5926545 .1769285 -3.35 0.001 -.939428 -.245881
-------------+----------------------------------------------------------------
Variance |
sigma2_e | .0396852 .004072 9.75 0.000 .0317042 .0476662
-------------+----------------------------------------------------------------
LR_Direct |
lnmvalue | .3747412 .0854161 4.39 0.000 .2073287 .5421536
lnkstock | .1274166 .0350247 3.64 0.000 .0587695 .1960638
-------------+----------------------------------------------------------------
LR_Indirect |
lnmvalue | .2894559 .254896 1.14 0.256 -.210131 .7890428
lnkstock | .2878004 .1273755 2.26 0.024 .038149 .5374517
-------------+----------------------------------------------------------------
LR_Total |
lnmvalue | .6641971 .2879684 2.31 0.021 .0997893 1.228605
lnkstock | .415217 .1438093 2.89 0.004 .1333558 .6970781
------------------------------------------------------------------------------
(est31 stored)
模型不收敛,通过 copy() 调整初始值,代码如下
. eststo:xsmle lninvest lnmvalue lnkstock,fe ///
model(sdm) wmat(WW) type(both) effects nolog ///
from(0.3995296 0.1598841 0.6188835 0.5201294 0.689 0.0396793,copy)
. Warning: All regressors will be spatially lagged
Computing marginal effects standard errors using MC simulation...
SDM with spatial and time fixed-effects Number of obs = 200
Group variable: id Number of groups = 10
Time variable: year Panel length = 20
R-sq: within = 0.6420
between = 0.8481
overall = 0.6868
Mean of fixed-effects = -3.0978
Log-likelihood = 34.2412
------------------------------------------------------------------------------
lninvest | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Main |
lnmvalue | .3992206 .09085 4.39 0.000 .2211578 .5772834
lnkstock | .1580265 .0430199 3.67 0.000 .0737089 .242344
-------------+----------------------------------------------------------------
Wx |
lnmvalue | .6083891 .3931709 1.55 0.122 -.1622116 1.37899
lnkstock | .5087355 .2099962 2.42 0.015 .0971505 .9203204
-------------+----------------------------------------------------------------
Spatial |
rho | -.5929535 .1769972 -3.35 0.001 -.9398616 -.2460454
-------------+----------------------------------------------------------------
Variance |
sigma2_e | .0397628 .0040881 9.73 0.000 .0317502 .0477754
-------------+----------------------------------------------------------------
LR_Direct |
lnmvalue | .3747347 .0854988 4.38 0.000 .2071601 .5423092
lnkstock | .1274166 .0350578 3.63 0.000 .0587046 .1961286
-------------+----------------------------------------------------------------
LR_Indirect |
lnmvalue | .2894315 .2550993 1.13 0.257 -.2105539 .7894169
lnkstock | .2877979 .1274783 2.26 0.024 .0379451 .5376507
-------------+----------------------------------------------------------------
LR_Total |
lnmvalue | .6641662 .2881908 2.30 0.021 .0993227 1.22901
lnkstock | .4152145 .1439223 2.88 0.004 .133132 .697297
------------------------------------------------------------------------------
(est32 stored)
至此,本文讲解了空间权重矩阵构造和静态空间面板数据模型估计。此外,还有模型的选择(SDM vs SAR vs SEM),大家可以参考「 Spatial panel-data models using Stata 」。
此外,动态空间面板模型估计可以通过调整dlag选项进行定义:
-
dlag(1): y t = τ y t − 1 + ρ W y t + x t β + W x t θ + a + λ t ι n + ε t y_{t}=\tau y_{t-1} + \rho W y_{t}+x_{t} \beta+W x_{t} \theta+a+\lambda_{t} \iota_{n}+\varepsilon_{t} yt=τyt−1+ρWyt+xtβ+Wxtθ+a+λtιn+εt
-
dlag(2): y t = ψ W y t − 1 + ρ W y t + x t β + W x t θ + a + λ t ι n + ε t y_{t}=\psi W y_{t-1}+ \rho W y_{t}+x_{t} \beta+W x_{t} \theta+a+\lambda_{t} \iota_{n}+\varepsilon_{t} yt=ψWyt−1+ρWyt+xtβ+Wxtθ+a+λtιn+εt
-
dlag(3): y t = τ y t − 1 + ψ W y t − 1 + ρ W y t + x t β + W x t θ + a + λ t ι n + ε t y_{t}=\tau y_{t-1} + \psi W y_{t-1}+ \rho W y_{t}+x_{t} \beta+W x_{t} \theta+a+\lambda_{t}\iota_{n}+\varepsilon_{t} yt=τyt−1+ψWyt−1+ρWyt+xtβ+Wxtθ+a+λtιn+εt
5.4. 地理分布图及 Moran 指数图
除了基本的模型估计,有时也会在论文中放上一些比较酷炫的图形,比如变量的地理分布图,可以利用 spmap 命令进行实现。提示:以下程序利用 Stata 12 版本实现,我发现 spmap 这个命令在 15 版本运行会出错,需要进行软件更新。
cd "H:\"
use sample_sp,clear
bys countries: egen invest_mean=mean(invest)
bys countries: egen mvalue_mean=mean(mvalue)
bys countries: egen kstock_mean=mean(kstock)
bys countries:keep if _n==1
save mean_sample_sp.dta,replace
cd "H:\Data_Extract_From_World_Development_Indicators"
shp2dta using "TM_WORLD_BORDERS_SIMPL-0.2.shp", ///
database(data_db) coordinates(data_xy) ///
genid(id) gencentroids(c) replace
use data_db, clear
rename NAME countries
list countries LAT LON in 1/10
merge 1:m countries using "H:\mean_sample_sp.dta"
local omit invest_mean mvalue_mean kstock_mean
foreach x of local omit {
replace `x' = 0 if missing(`x')
}
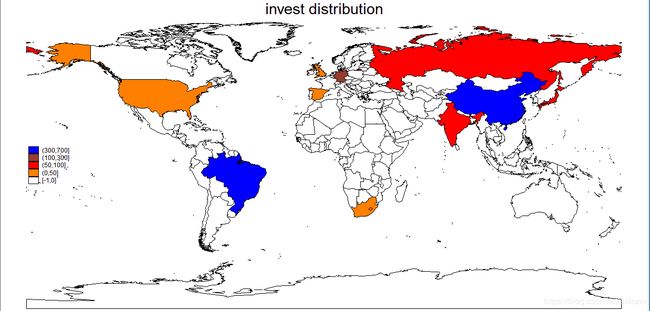
spmap invest_mean using data_xy.dta, ///
id(id) fcolor(white orange red maroon blue) ///
legend(position(9)) ///
title("invest distribution") ///
clbreaks(-1 0 50 100 300 700) ///
clmethod(custom)
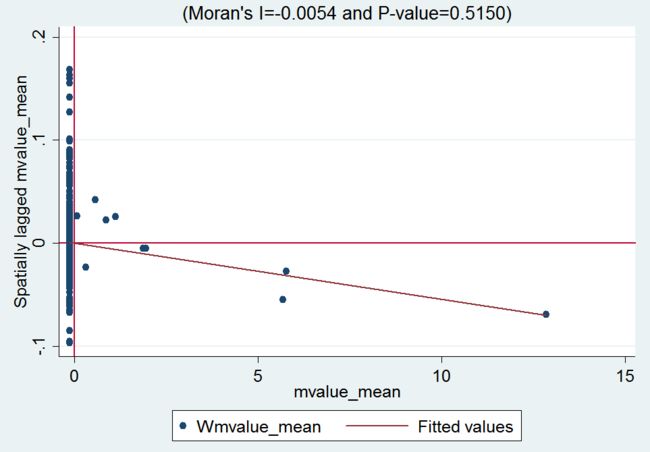
通常在模型估计之前,可以利用 Moran 指数进行空间相关判断,这里利用 splagvar 命令进行计算并绘图
cd "H:\"
use spatial_weight.dta,clear
spwmatrix gecon LAT LON, wn(example_w2) wtype(inv) ///
r(3958.761) alpha(1) xport(example_w2,txt) ///
mataf row replace /*此处加了mataf选项,用于生成Mata格式矩阵*/
local xlist mvalue_mean
splagvar `xlist', wname("example_w2") wfrom(Mata) ///
moran(`xlist') plot(`xlist') replace
graph export "`xlist'.tif",replace
几点说明
-
利用
xsmle命令有时会出现 3200 conformability error,这个错误可能原因有几种:空间权重矩阵维数和数据维数不一致;数据存在缺失值;空间权重矩阵未标准化。此外,若出现 initial values not feasible, 可以利用 copy 选项进行调整。 -
目前空间计量模型的实现工具已经很成熟,之前主要还是利用 Matlab 中 jplv7 (https://www.spatial-econometrics.com),以及 R 软件中的 spdep和splm包。近年来,在 Stata 中相应的命令发展很快,特别是 Stata 15 版本后,已将其纳入官方命令。本推文主要是基于Stata Journal发表的外部命令
xsmle进行说明,请大家进一步参考官方命令spxtregress。 -
在利用空间计量模型进行实证分析时,建议利用多种空间权重矩阵进行稳健性比较。
-
不能仅通过空间自相关系数 ρ \rho ρ 来判断是否存在空间溢出效应,应该通过间接效应进行判断。
参考文献
- Belotti F, Hughes G, Mortari A P. Spatial panel-data models using Stata[J]. The Stata Journal, 2017, 17(1): 139-180. [PDF]
- LeSage, J. P. & Pace, R. K. Introduction to Spatial Econometrics, Boca Raton, Taylor & Francis, 2009.
- Golgher A B, Voss P R. How to interpret the coefficients of spatial models: Spillovers, direct and indirect effects[J]. Spatial Demography, 2016, 4(3): 175-205.
- Lee L, Yu J. QML estimation of spatial dynamic panel data models with time varying spatial weights matrices[J]. Spatial Economic Analysis, 2012, 7(1): 31-74.
- Palombi S, Perman R, Tavéra C. Commuting effects in O kun’s L aw among B ritish areas: Evidence from spatial panel econometrics[J]. Papers in Regional Science, 2017, 96(1): 191-209.
- 刘迪. Stata空间溢出效应的动态图形 (空间计量).
- 游万海, 连玉君. Stata: 外部命令的搜索、安装与使用.
- 游万海, 连玉君. Stata: 面板数据模型-一文读懂.
关于我们
- 「Stata 连享会」 由中山大学连玉君老师团队创办,定期分享实证分析经验, 公众号:StataChina。
- 公众号推文同步发布于 CSDN 、简书 和 知乎Stata专栏。可在百度中搜索关键词 「Stata连享会」查看往期推文。
- 点击推文底部【阅读原文】可以查看推文中的链接并下载相关资料。
- 欢迎赐稿: 欢迎赐稿。录用稿件达 三篇 以上,即可 免费 获得一期 Stata 现场培训资格。
- E-mail: [email protected]
- 往期推文:计量专题 || 精品课程 || 简书推文 || 公众号合集
![]()
![]()