六、【机器学习作业】正则化线性回归和偏差\方差(python版ex5)
正则化线性回归和偏差\方差(ex5)
- (一)正则化线性回归 Regularized Linear Regression
- (1)可视化数据集 Visualizing the dataset
- (2)正则化线性回归代价函数 Regularized linear regression cost function
- (3)正则化线性回归梯度 Regularized linear regression gradient
- (4)拟合线性回归 Fitting linear regression
- (二)偏差与方差 Bias-variance
- (1)学习曲线 Learning curves
- (三)多项式回归 Polynomial regression
- (1)学习多项式回归 Learning Polynomial Regression
- (2)调整正则化参数 Adjusting the regularization parameter
- (3)通过交叉验证集选择λ Selecting λ using a cross validation set
- (4)计算测试集误差 Computing test set error
(一)正则化线性回归 Regularized Linear Regression
在练习的前半部分中,您将使用水库水位的变化来实现正则化线性回归,以预测大坝流出的水量。在后半部分中,您将对调试学习算法进行一些诊断,并检查偏差V.S方差的影响。
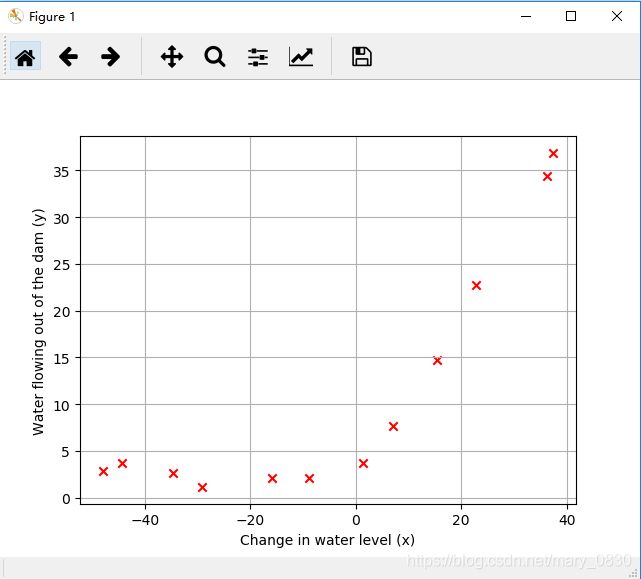
(1)可视化数据集 Visualizing the dataset
机器学习课程提供的数据集中,包含水位变化的历史记录 X X X和流出大坝的水量 y y y。
首先将数据集分成三个部分:
| 名称 | 参数 |
|---|---|
| 训练集 (训练模型) | X X X, y y y |
| 交叉验证集(用于决定正则化参数) | X v a l Xval Xval, y v a l yval yval |
| 测试集(用于评估表现) | X t e s t Xtest Xtest, y t e s t ytest ytest |
跟之前一样,首先导入所需要的库:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
from scipy.io import loadmat
from sklearn.metrics import classification_report #用于评价报告
载入数据集,以及可视化这些数据:
def load_mat(path):
'''读取.mat数据'''
data = loadmat(path)
X, y = data['X'], data['y']
Xval, yval = data['Xval'], data['yval']
Xtest, ytest = data['Xtest'], data['ytest']
#添加偏置单元
X_1 = np.insert(X ,0,1,axis=1)
Xval = np.insert(Xval ,0,1,axis=1)
Xtest = np.insert(Xtest,0,1,axis=1)
print('X={},y={}'.format(X_1.shape, y.shape))
print('Xval={},yval={}'.format(Xval.shape, yval.shape))
print('Xtest={},ytest={}'.format(Xtest.shape, ytest.shape))
return X,y,Xval,yval,Xtest,ytest
def plot_data():
'''可视化数据'''
plt.figure()
plt.scatter(X[:,1:],y,c='r',marker='x')
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.grid() #显示网格
plt.show()
path = 'ex5data1.mat'
X,y,Xval,yval,Xtest,ytest = load_mat(path)
plot_data()
运行结果为: 显示数据集内所有数据的维度数
X=(12, 2),y=(12, 1)
Xval=(21, 2),yval=(21, 1)
Xtest=(21, 2),ytest=(21, 1)
(2)正则化线性回归代价函数 Regularized linear regression cost function
表达式为:
J ( θ ) = 1 2 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ) + λ 2 m ( ∑ j = 1 n θ j 2 ) J(\theta )=\frac{1}{2m}\left (\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}\right )+\frac{\lambda }{2m}\left ( \sum_{j=1}^{n}\theta _{j}^{2}\right ) J(θ)=2m1(i=1∑m(hθ(x(i))−y(i))2)+2mλ(j=1∑nθj2)
函数代码为:
def reg_cost(theta, X, y, l):
'''不需要正则化第一项theta0(即偏置单元)'''
cost = np.sum((np.dot(X,theta) - y.flatten()) ** 2)
regularized = l * (theta[1:] @ theta[1:])
return (cost + regularized) / (2 * len(X))
theta = np.ones(X.shape[1])
print('regression cost function:',reg_cost(theta, X, y, 1))
计算结果:
Regularized linear regression cost function: 303.9931922202643
该结果与预测得到的结果相符,说明该代码正确。
(3)正则化线性回归梯度 Regularized linear regression gradient
数学公式为:
当 j = 0 j=0 j=0时,
∂ J ( θ ) ∂ θ 0 = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J(\theta )}{\partial\theta _{0}}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}_{j} ∂θ0∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)
当 j ≥ 1 j≥1 j≥1时,
∂ J ( θ ) ∂ θ 0 = ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j \frac{\partial J(\theta )}{\partial\theta _{0}}=\left ( \frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}_{j} \right )+\frac{\lambda }{m}\theta _{j} ∂θ0∂J(θ)=(m1i=1∑m(hθ(x(i))−y(i))xj(i))+mλθj
正则化的梯度代码为:
def reg_gradient(theta, X, y, l):
'''计算正则化的梯度'''
#grad = np.sum(np.dot(np.dot(X,theta) - y.flatten(),X))
grad = np.dot(np.dot(X,theta) - y.flatten(),X)
regularized = l * theta
regularized[0] = 0 #不需要正则化theta0
return (grad + regularized) / len(X)
theta = np.ones(X.shape[1])
print('Regularized linear regression gradient:',reg_gradient(theta, X, y, 1))
Regularized linear regression gradient: [-15.30301567 598.25074417]
该结果与预测得到的结果相符,说明该代码正确。
(4)拟合线性回归 Fitting linear regression
编写拟合线的代码:
def Fitting_linear_regression(X, y, l):
theta = np.zeros(X.shape[1])
res = opt.minimize(fun = reg_cost,
x0 = theta,
args = (X,y,1),
method = 'TNC',
jac = reg_gradient,
options={'maxiter':400})
return res.x
fit_lin_reg = Fitting_linear_regression(X, y, 1)
plot_data()
plt.plot(X[:,1:],np.dot(X,fit_lin_reg))
训练集上拟合的结果:

这里把 λ = 0 \lambda = 0 λ=0(相当于不使用正则化)。由于原始输入只有1个特征,所以拟合效果不是很好,之后在原始输入特征的基础上增加多项式特征。
(二)偏差与方差 Bias-variance
机器学习中的一个重要概念是偏差与方差的权衡。具有高偏差的模型对于数据来说不够复杂,容易出现下溢现象(欠拟合),而具有高方差的模型则与训练数据过度匹配(过拟合)。总结:高偏差(欠拟合),高方差(过拟合)。
(1)学习曲线 Learning curves
为了绘制学习曲线,需要一个训练集和交叉验证集,并训练这两个集合的误差随着样本 m m m变化,通过变化情况来判断是否欠拟合或者过拟合。
具体来说,使用训练集的 m m m个子集来训练模型,得到不同的 θ \theta θ值,然后求 m m m个样本的训练集误差和交叉验证集误差(此时不使用正则化, λ = 0 \lambda=0 λ=0)。注意的是,计算交叉验证代价时需要整个交叉验证集来计算,无需分为子集。
数据集的训练误差定义为:
J t r a i n ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ] J_{train}(\theta )=\frac{1}{2m}\left [ \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)}) ^{2}\right ] Jtrain(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2]
编写学习曲线的代码,并运行该函数代码:
def learning_curve(X, y, Xval, yval, l):
'''绘制学习曲线,即交叉验证误差与训练误差随着样本数量的变化而变化'''
XX = range(1, len(X) + 1) #至少有一个数
err_train, err_val = [], []
for i in XX:
theta = Fitting_linear_regression(X[:i], y[:i], l)
err_train_i = reg_cost(theta, X[:i], y[:i], 0)
err_val_i = reg_cost(theta, Xval, yval, 0)
err_train.append(err_train_i)
err_val.append(err_val_i)
plt.figure()
plt.plot(XX,err_train,label = 'Training Cost')
plt.plot(XX,err_val,label = 'Cross Validation Cost')
plt.title('Learning curve for linear regression')
plt.legend(['Train','Cross Validation'])
plt.xlabel('Number of training examples')
plt.ylabel('Error')
plt.grid() #显示网格
plt.axis([0,13,0,150])
plt.show()
learning_curve(X, y, Xval, yval, 0)
根据训练集与交叉验证集所绘制的学习曲线:

说明: 验证误差随样本增加不断减小,并趋于平缓;训练误差随样本增加不断增大,最后也趋于平缓;并且二者非常接近,交界处对应的误差比较大。根据学习曲线的特点,此时模型出现了高偏差(欠拟合)的情况。那么增加更多的训练样本作用并不大,因此,应该增加更多的输入特征。
(三)多项式回归 Polynomial regression
根据上一个例子产生的问题,线性模型对于有些数据来说太简单了,因此导致了欠拟合的情况,在这部分,添加一些特征来解决以上的不足。
多项式回归的假设函数定义为:
h θ ( x ) = θ 0 + θ 1 ∗ ( w a t e r L e v e l ) + θ 2 ∗ ( w a t e r L e v e l ) 2 + ⋯ + θ p ∗ ( w a t e r L e v e l ) p = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ p x p \begin{aligned} h_{\theta }(x) &=\theta _{0}+\theta _{1}*(waterLevel)+\theta _{2}*(waterLevel)^{2}+\cdots +\theta _{p}*(waterLevel)^{p} \\ &=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+\cdots +\theta _{p}x_{p} \end{aligned} hθ(x)=θ0+θ1∗(waterLevel)+θ2∗(waterLevel)2+⋯+θp∗(waterLevel)p=θ0+θ1x1+θ2x2+⋯+θpxp
(1)学习多项式回归 Learning Polynomial Regression
把多项式高阶项看作特征,因此多项式回归其本质是多特征的线性回归。
首先进行数据预处理,把X,Xval,Xtest都添加多项式特征(分别都添加到6次方),并对数据进行标准化。
编写添加多项式以及处理数据的代码:
def polyFeatures(X, power):
'''添加多项式特征,在array的最后一列添加第二列的i+2次方(第一列为偏置单元),
从二次方开始添加(由于数据本身含有一列一次方)'''
Xpoly = X.copy()
for i in range(2, power + 1):
Xpoly = np.insert(Xpoly, Xpoly.shape[1], np.power(Xpoly[:,1], i), axis=1)
return Xpoly
def get_means_std(X):
'''获取训练集的均值和误差,用来标准化所有训练集的数据'''
means = np.mean(X, axis = 0)
stds = np.std(X, axis = 0, ddof = 1) #ddof = 1,means样本标准差
return means, stds
def feature_Normalize(myX, means, stds):
'''归一化'''
X_norm = myX.copy()
X_norm[:,1:] = X_norm[:,1:] - means[1:]
X_norm[:,1:] = X_norm[:,1:] / stds[1:]
return X_norm
说明: 数据处理是对数据进行归一化处理,即将所有数据集内的数据都用训练集的均值和样本标准差进行处理,所以要将训练集的均值和样本标准差储存起来,用于后面的数据处理。归一化的计算公式为: x i = x i − m e a n s t d x_{i}=\frac{x_{i}-mean}{std} xi=stdxi−mean。这里用的是样本标准差,用np.std()中的ddof = 1表示样本标准差,默认ddof = 0是总体标准差。而pandas默认计算样本标准差。
编写增加特征后进行训练,并可视化拟合效果以及学习曲线的代码:
power = 6 #在实验中,将特征扩展到6次方
train_means,train_stds = get_means_std(polyFeatures(X, power))
X_norm = feature_Normalize(polyFeatures(X, power), train_means, train_stds)
Xval_norm = feature_Normalize(polyFeatures(Xval, power), train_means, train_stds)
Xtest_norm = feature_Normalize(polyFeatures(Xtest, power), train_means, train_stds)
def plot_fit(means, stds, l):
'''绘制拟合曲线'''
theta = Fitting_linear_regression(X_norm, y, l)
X = np.linspace(-80,80,50)
Xmat = X.reshape(-1,1)
Xmat = np.insert(Xmat, 0, 1, axis = 1)
x_mat = polyFeatures(Xmat, power)
x_mat_norm = feature_Normalize(x_mat, means, stds)
plot_data()
plt.plot(X,np.dot(x_mat_norm,theta),'g--')
plot_fit(train_means, train_stds, 0)
learning_curve(X_norm, y, Xval_norm, yval, 0)
绘制拟合曲线以及学习曲线的结果:
当 λ = 0 \lambda=0 λ=0时,训练误差太小,产生过拟合的情况。
(2)调整正则化参数 Adjusting the regularization parameter
调整正则化的参数 λ \lambda λ,观察数据拟合情况。
当 λ = 1 \lambda=1 λ=1时,拟合情况比较好一些。
plot_fit(train_means, train_stds, 1)
learning_curve(X_norm, y, Xval_norm, yval, 1)

当 λ = 100 \lambda=100 λ=100时,产生了欠拟合(高偏差)的情况。
plot_fit(train_means, train_stds, 100)
learning_curve(X_norm, y, Xval_norm, yval, 100)
(3)通过交叉验证集选择λ Selecting λ using a cross validation set
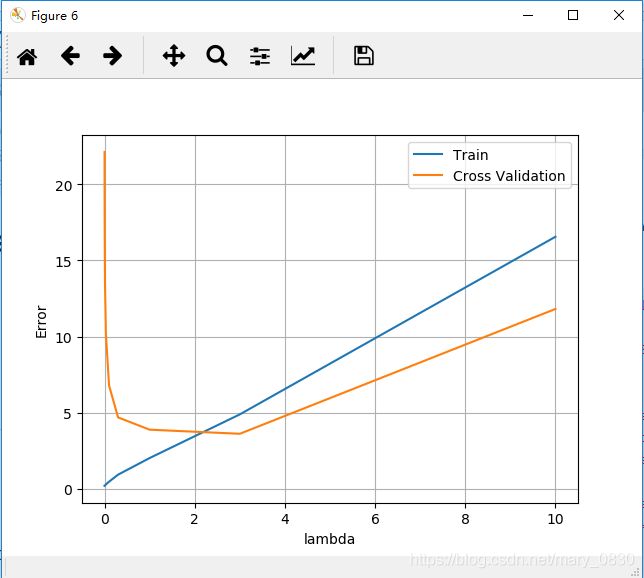
使用不同 λ \lambda λ值,可视化训练误差和交叉验证误差的曲线:
def validation_curve(X, y, Xval, yval):
'''使用不同的lambda值,并可视化曲线'''
lambdas = np.array([0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10])
error_train, error_val = [], []
for l in lambdas:
theta = Fitting_linear_regression(X_norm, y, l)
error_train.append(reg_cost(theta, X_norm, y, l))
error_val.append(reg_cost(theta, Xval_norm, yval, l))
plt.figure()
plt.plot(lambdas,error_train,label='Train')
plt.plot(lambdas,error_val,label='Cross Validation')
plt.legend()
plt.xlabel('lambda')
plt.ylabel('Error')
plt.grid(True)
plt.show()
validation_curve(X, y, Xval, yval)
运行结果为: 可以看出在 λ = 3 \lambda = 3 λ=3时,在该点取到代价最小值,交叉验证集的代价最小。
(4)计算测试集误差 Computing test set error
theta = Fitting_linear_regression(X_norm, y, 3)
print('test cost(l={}) = {}'.format(3, reg_cost(theta, Xtest_norm, ytest, 0)))
当power=6时,得到下面的数值:
test cost(l=3) = 4.755272015678817
test cost(l=3) = 3.8598814429362758