SFM三维重建(Python+OpenCV)
一、基础矩阵原理
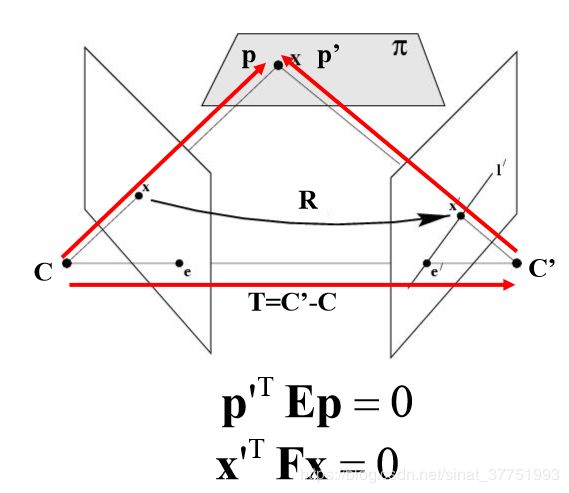
类似于单应性矩阵,当存在噪声和不正确的匹配时,我们需要估计基础矩阵。与单应性矩阵估计相比,基础矩阵增加了默认的最大迭代次数,改变了匹配的阈值,使其匹配更加精准。基础矩阵描述了空间中的点在两个像平面中的坐标对应关系,不仅包含了本质矩阵E的两个摄像机相关的旋转平移信息,还包含了两个摄像机的内参。可用于简化匹配,去除错配特征。
具体公式的推导,参考博客:https://blog.csdn.net/kokerf/article/details/72191054#commentBox
https://www.cnblogs.com/wangguchangqing/p/8214032.html
二、实验流程
1、检测特征点,然后在两幅图像间匹配
用SIFT算法实现两幅图像的特征点检测,找到对应的匹配点并绘制出来
2、由匹配计算基础矩阵
使用RANSAC方法估计最佳基础矩阵F,以及正确点的索引
3、由基础矩阵计算照相机矩阵
在两个视图的场景中,照相机矩阵可以由基础矩阵恢复出来。在没有任何照相机内参数知识的情况下,照相机矩阵只能通过射影变换恢复出来。因此,在无标定的情况下,第二个照相机矩阵可以使用一个(3*3)的射影变换出来。
假设第一个相机矩阵: P1=[I|0] ,第二相机矩阵: P2=[M | e′]
其中 e′ 是极点 (e′T F= 0), M = [e′×]F, e′× 是e的叉积
4、三角剖分这些三维点
从照相机矩阵的列表中,对正确点的三维点进行三角剖分,挑选出经过三角剖分后,在两个照相机前均含有最多场景点,即取出真正在照相机前面的点。
三、代码
# coding: utf-8
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from PCV.geometry import homography, camera,sfm
from PCV.localdescriptors import sift
camera = reload(camera)
homography = reload(homography)
sfm = reload(sfm)
sift = reload(sift)
# 载入图像,并计算特征
im1 = array(Image.open('b1.jpg'))
sift.process_image('b1.jpg', 'im1.sift')
im2 = array(Image.open('b2.jpg'))
sift.process_image('b2.jpg', 'im2.sift')
l1, d1 = sift.read_features_from_file('im1.sift')
l2, d2 = sift.read_features_from_file('im2.sift')
#匹配特征
matches = sift.match_twosided(d1, d2)
ndx = matches.nonzero()[0]
#使用齐次坐标表示
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)
d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()
figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()
#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
""" 使用RANSAN方法,从点对应中稳健地估计基础矩阵F
输入:使用齐次坐标表示的点x1,x2(3*n的数组)
输出:最佳基础矩阵F,以及正确点的索引"""
from PCV.tools import ransac
data = np.vstack((x1, x2))
d = 10 # 20 is the original
# 计算F,并返回正确点索引
F, ransac_data = ransac.ransac(data.T, model,
8, maxiter, match_threshold, d, return_all=True)
return F, ransac_data['inliers']
# 使用RANSAC方法估计最佳基础矩阵F,以及正确点的索引
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-5)
print F
#由基础矩阵计算第二个照相机矩阵
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)
print P2
# 三角剖分正确点,并移除不在所有照相机面前的点
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)
# 绘制三维点
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)
figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))
imshow(imj)
cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
if (0<= x1p[0][i]四、运行结果分析
1、室外场景(集美大学由湖对岸向东大门方向拍摄)
用SIFT算法进行的特征提取与匹配
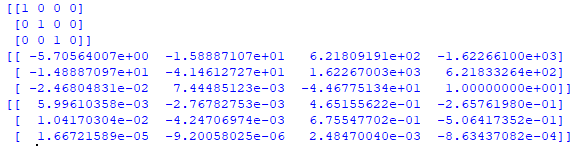
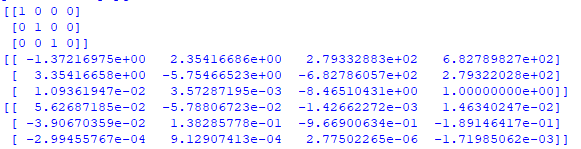
计算出基础矩阵F和第二个照相机矩阵P2
经过三角剖分后,第一个照相机和第二个照相机均含有最多场景点的匹配结果
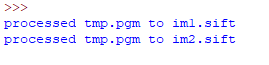
第三张图片生成的SIFT文件
![]()
经过三角剖分后,第一个照相机和第三个照相机均含有最多场景点的匹配结果
计算出第一个照相机矩阵p1,第二个照相机矩阵p2,第三照相机矩阵p3的值
2、室内场景(集美大学陆大楼机房)
用SIFT算法进行的特征提取与匹配
计算出基础矩阵F和第二个照相机矩阵P2
经过三角剖分后,第一个照相机和第二个照相机均含有最多场景点的匹配结果
第三张图片生成的SIFT文件
![]()
经过三角剖分后,第一个照相机和第三个照相机均含有最多场景点的匹配结果
经过三角剖分后,第一个照相机和第三个照相机均含有最多场景点的匹配结果
3、注意点
在拍摄图片时,要从不同视角拍摄同一处物体,例如:手持相机,面向拍摄的物体,大致呈水平移动的拍摄,尽可能拍摄有明显特征的场景,最好避免拍摄对称的建筑,无明显特征的场景,否者可能会出现匹配点数目不够的错误
还有为了要找到最佳的基础矩阵,要循环计算5000次,为了减少运行的时间,要将拍摄的照片进行压缩缩小。