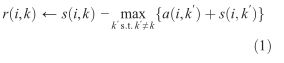浅谈AP聚类算法-matlab
AP(Affinity Propagation)算法,称为仿射传播聚类算法、近邻传播聚类算法、亲和传播聚类算法,是根据数据点之间的相似度来进行聚类,可以是对称的,也可以是不对称的。 该算法不需要先确定聚类的数目,而是把所有的数据点都看成潜在意义上的聚类中心(exemplar).这有别于K-means等聚类。
1.Clustering by Passing Messages Between Data Points 文章微译
在后面的迭代中,由下面的更新规则规定,当一些点被有效地分配给其他聚类中心,他们的availabilities将会降到零下。这些负的availabilities会减小上面规则中的一些输入相似度s(i,k′) 的有效值,从竞争中去掉相应的候选聚类中心。由于k=i,responsibilities r(k,k)被设置成k被选作为聚类中心的输入的preference(s(k,k))减去点i和其他所有候选聚类中心的最大相似度。这个"self-responsibility"基于输入合适的preference,通过表明k多么不合适分配给另一个聚类中心,来反映k是一个聚类中心的累积证据。鉴于上面的responsibility的更新让所有的候选簇中心竞争数据点的控制权,下面的availibility更新从数据点积累关于是否每个候选聚类中心都会是一个好的聚类中心的证据。
availability a(i,k)被设置成self-responsibility r(k,k)加上从其他点获得的正responsibilities候选聚类中心k的总和。只有正responsibilities部分是会被添加进来的,因为对于一个好的聚类中心正responsibilities是必要的。不管负的responsibilities多么不适合的程度。如果self-responsibility r(k,k)是负的(表明点k目前更适合作为另一个簇中心点的归属点比作为一个簇中心点)。如果一些其他点支持点k作为它们的簇中心,k作为一个簇中心点的availibility能够增加。
为了限制得到的正responsibilities的强烈影响,这个总和是被限定的,它不能大于0.”self-availability”a(k,k)的更新是不一样的:![]()
基于正responsibilities从其他点传递给候选聚类中心,这个信息反映了点k是一个聚类中心的积累证据。
以上更新规律要求是最简单的,本地计算机很容易实现,并且消息只需要在已知的相似度的点之间交换。在AP算法实现的过程中任何点的availabilities和responsibilities都与定义聚类中心相关联。对于点i,a(i,k)+r(i,k)取最大值时的k值,如果k=i时,确定点i作为一个聚类中心,否则确定数据点k是点id聚类中心。超过一个固定的迭代次数或消息的变化小于一个阈值或本地决定对一些迭代数量保持不变时,消息的传递过程将会被终止。当更新消息时,它们被阻尼去避免出现在某些情况下的数据振荡是重要的。每个消息被设置为先前迭代里它的值的l倍加上它规定的更新值的(1- l)倍,且阻尼系数l的值在0和1之间。在我们所有的实验里,我们用一个缺省的阻尼系数l=0.5,并且每个AP迭代都由更新所有被给了availabilities的responsibilities,更新所有被给了responsibilities的availabilities以及结合availibilities和responsibilities去监视聚类中心的决定和当这些决定不再改变时终止算法。
Figure1A展示了AP应用于25个两维数据点的运动过程,用负平方差作为相似度。AP的一个优点是聚类中心的数量不用预先指定。反而,合适的聚类中心的数量从信息传递方法中产生并且取决于聚类中心参数(preference)。这能够自动化模型选择是基于前面的对每个点如何作为聚类中心才合适的描述。Figure1D展示了输入的共同的preference的值对产生簇的数目的影响。这个关系几乎和通过精确地最小化平方差去发现的关系是一样的。
ps: 本人英语水平不高,以上翻译仅个人理解,不恰当不正确之处,还请包容理解并指出。2.以下以最简单的六个点进行聚类为例,分析AP算法实现的基本步骤和核心思想:
clear all;close all;clc; %清除所有变量,关闭所有窗口, 清除命令窗口的内容
x=[1,0; %定义一个矩阵
1,1;
0,1;
4,1;
4,0;
5,1];
N=size(x,1); %N为矩阵的列数,即聚类数据点的个数
M=N*N-N; %N个点间有M条来回连线,考虑到从i到k和从k到i的距离可能是不一样的
s=zeros(M,3); %定义一个M行3列的零矩阵,用于存放根据数据点计算出的相似度
j=1; %通过for循环给s赋值,第一列表示起点i,第二列为终点k,第三列为i到k的负欧式距离作为相似度。
for i=1:N
for k=[1:i-1,i+1:N]
s(j,1)=i;s(j,2)=k;
s(j,3)=-sum((x(i,:)-x(k,:)).^2);
j=j+1;
end;
end;
p=median(s(:,3)); %p为矩阵s第三列的中间值,即所有相似度值的中位数,用中位数作为preference,将获得数量合适的簇的个数
tmp=max(max(s(:,1)),max(s(:,2))); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
S=-Inf*ones(N,N); %-Inf负无穷大,定义S为N*N的相似度矩阵,初始化每个值为负无穷大
for j=1:size(s,1) %用for循环将s转换为S,S(i,j)表示点i到点j的相似度值
S(s(j,1),s(j,2))=s(j,3);end;
nonoise=1; %此处仅选择分析无噪情况(即S(i,j)=S(j,i)),所以略去下面几行代码
%if ~nonoise %此处几行注释掉的代码是 在details,sparse等情况下时为了避免使用了无噪数据而使用的,用来给数据添加noise
%rns=randn('state');
%randn('state',0);
%S=S+(eps*S+realmin*100).*rand(N,N);
%randn('state',rns);
%end;
%Place preferences on the diagonal of S
if length(p)==1 %设置preference
for i=1:N
S(i,i)=p;
end;
else
for i=1:N
S(i,i)=p(i);
end;
end;
% Allocate space for messages ,etc
dS=diag(S); %%%%%%%%%%%%%%%%列向量,存放S中对角线元素信息
A=zeros(N,N);
R=zeros(N,N);
%Execute parallel affinity propagation updates
convits=50;maxits=500; %设置迭代最大次数为500次,迭代不变次数为50
e=zeros(N,convits);dn=0;i=0; %e循环地记录50次迭代信息,dn=1作为一个循环结束信号,i用来记录循环次数
while ~dn
i=i+1;
%Compute responsibilities
Rold=R; %用Rold记下更新前的R
AS=A+S %A(i,j)+S(i,j)
[Y,I]=max(AS,[],2) %获得AS中每行的最大值存放到列向量Y中,每个最大值在AS中的列数存放到列向量I中 for k=1:N
AS(k,I(k))=-realmax; %将AS中每行的最大值置为负的最大浮点数,以便于下面寻找每行的第二大值
end;
[Y2,I2]=max(AS,[],2); %存放原AS中每行的第二大值的信息
R=S-repmat(Y,[1,N]); %更新R,R(i,k)=S(i,k)-max{A(i,k')+S(i,k')} k'~=k 即计算出各点作为i点的簇中心的适合程度
for k=1:N %eg:第一行中AS(1,2)最大,AS(1,3)第二大,
R(k,I(k))=S(k,I(k))-Y2(k); %so R(1,1)=S(1,1)-AS(1,2); R(1,2)=S(1,2)-AS(1,3); R(1,3)=S(1,3)-AS(1,2).............
end; %这样更新R后,R的值便表示k多么适合作为i 的簇中心,若k是最适合i的点,则R(i,k)的值为正
lam=0.5;
R=(1-lam)*R+lam*Rold; %设置阻尼系数,防止某些情况下出现的数据振荡
%Compute availabilities
Aold=A;
Rp=max(R,0) %除R(k,k)外,将R中的负数变为0,忽略不适和的点的不适合程度信息
for k=1:N
Rp(k,k)=R(k,k);
end;
A=repmat(sum(Rp,1),[N,1])-Rp %更新A(i,k),先将每列大于零的都加起来,因为i~=k,所以要减去多加的Rp(i,k) dA=diag(A);
A=min(A,0); %除A(k,k)以外,其他的大于0的A值都置为0
for k=1:N
A(k,k)=dA(k);
end;
A=(1-lam)*A+lam*Aold; %设置阻尼系数,防止某些情况下出现的数据振荡
%Check for convergence
E=((diag(A)+diag(R))>0);
e(:,mod(i-1,convits)+1)=E; %将循环计算结果列向量E放入矩阵e中,注意是循环存放结果,即第一次循环得出的E放到N*50的e矩阵的第一列,第51次的结果又放到第一列
K=sum(E); %每次只保留连续的convits条循环结果,以便后面判断是否连续迭代50次中心簇结果都不变。%%%%%%%%%%%%%%%%
if i>=convits || i>=maxits %判断循环是否终止
se=sum(e,2); %se为列向量,E的convits次迭代结果和
unconverged=(sum((se==convits)+(se==0))~=N);%所有的点要么迭代50次都满足A+R>0,要么一直都小于零,不可以作为簇中心
if (~unconverged&&(K>0))||(i==maxits) %迭代50次不变,且有簇中心产生或超过最大循环次数时循环终止。
dn=1;
end;
end;
end;
I=find(diag(A+R)>0); %经过上面的循环,便确定好了哪些点可以作为簇中心点,用find函数找出那些簇1中心点,这个简单demo中I=[2,4],
K=length(I); % Identify exemplars %即第二个点和第四个点为这六个点的簇中心
if K>0 %如果簇中心的个数大于0
[~,c]=max(S(:,I),[],2); %取出S中的第二,四列;求出2,4列的每行的最大值,如果第一行第二列的值大于第一行第四列的值,则说明第一个点是第二个点是归属点
c(I)=1:K; % Identify clusters %c(2)=1,c(4)=2(第2个点为第一个簇中心,第4个点为第2个簇中心)
% Refine the final set of exemplars and clusters and return results
for k=1:K
ii=find(c==k); %k=1时,发现第1,2,3个点为都属于第一个簇
[y,j]=max(sum(S(ii,ii),1)); %k=1时 提取出S中1,2,3行和1,2,3列组成的3*3的矩阵,分别算出3列之和取最大值,y记录最大值,j记录最大值所在的列
I(k)=ii(j(1)); %I=[2;4]
end;
[tmp,c]=max(S(:,I),[],2); %tmp为2,4列中每行最大数组成的列向量,c为每个最大数在S(:,I)中的位置,即表示各点到那个簇中心最近
c(I)=1:K; %c(2)=1;c(4)=2;
tmpidx=I(c) %I=[2;4],c中的1用2替换,2用4替换
%(tmpidx-1)*N+(1:N)' %一个列向量分别表示S(1,2),S(2,2),S(3,2),S(4,4),S(5,4),S(6,4)是S矩阵的第几个元素
%sum(S((tmpidx-1)*N+(1:N)')) %求S中S(1,2)+S(2,2)+S(3,2)+S(4,4)+S(5,4)+S(6,4)的和
tmpnetsim=sum(S((tmpidx-1)*N+(1:N)')); %将各点到簇中心的一个表示距离的负值的和来衡量这次聚类的适合度
tmpexpref=sum(dS(I)); %dS=diag(S); %表示所有被选为簇中心的点的适合度之和
else
tmpidx=nan*ones(N,1); %nan Not A Number 代表不是一个数据。数据处理时,在实际工程中经常数据的缺失或者不完整,此时我们可以将那些缺失设置为nan
tmpnetsim=nan;
tmpexpref=nan;
end;
netsim=tmpnetsim; %反应这次聚类的适合度
dpsim=tmpnetsim-tmpexpref; %
expref=tmpexpref; %
idx=tmpidx; %记录了每个点所属那个簇中心的列向量
unique(idx);
fprintf('Number of clusters: %d\n',length(unique(idx)));
fprintf('Fitness (net similarity): %g\n',netsim);
figure; %绘制结果
for i=unique(idx)'
ii=find(idx==i);
h=plot(x(ii,1),x(ii,2),'o');
hold on;
col=rand(1,3);
set(h,'Color',col,'MarkerFaceColor',col);
xi1=x(i,1)*ones(size(ii));
xi2=x(i,2)*ones(size(ii));
line([x(ii,1),xi1]',[x(ii,2),xi2]','Color',col);
end;
axis equal ;
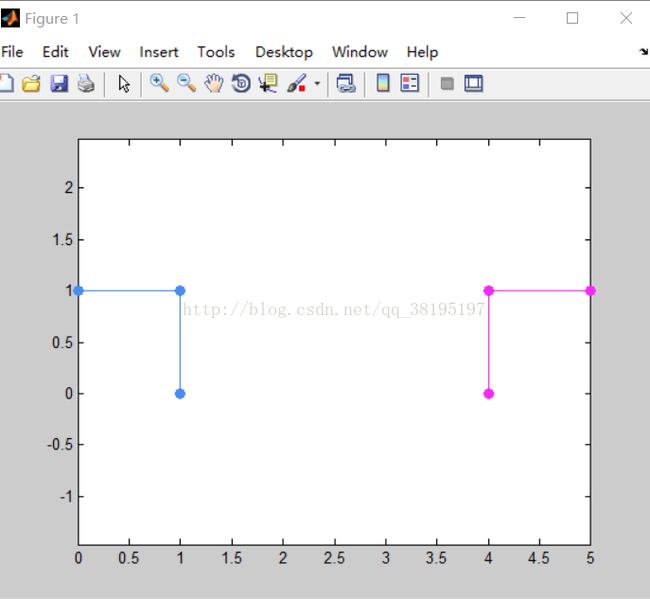
运行图像结果:
3.个人的理解(仅供参考)
①输入一组相似度,一般取相似度的中位数作为preference参数
②计算R和A。计算R时,R值确定k适合作为i的聚类中心的程度。R--先从i到k找出最适合作为i的聚类中心的点。(第一次循环时,到点i距离最近的点最适合作为i的聚类中心) A--计算其他点对R中找出的那些相对适合的点被选作聚类中心的支持程度的总和。受支持的R值置为零。最后用R(i,i)+A(i,i)>0来衡量点i是否可以作为聚类中心,若超过规定的迭代次数点i依旧是可以的或循环次数超过规定的最大循环次数,便可以跳出循环。
③由R+S>0来找出聚类中心点,再在S中寻找这些聚类中心的归属点。
④画出图像