Python实现图的经典DFS、BFS、Dijkstra、Floyd、Prim、Kruskal算法

       讲在前面的话，图的算法太多，理论知识肯定一篇博客讲不完，关于理论知识大家可以参考教材Sedgewick的《算法》或reference的链接,本文主要还是想在一篇博客中记录六种算法的Python代码。同样想吐槽一下，虽然网上博客很多，但是并不代表他们的代码都是正确的，还是要看经典教材啊，教材这么多人在用，所以出现错的概率会低一些。在这讲一下自己对这些算法的核心思想的一些个人理解，很多东西细节是记不住的，本科学了两遍算法，现在不也一样重头再学么，但算法的核心思想这是可以记住的，希望我的理解对别人会有一点点用处。

1.个人的一点理解

       对于DFS和BFS，如果遇到搜索和遍历，肯定要想到堆栈和队列，而遇到堆栈肯定就要想到是不是可以用递归来实现，因为递归程序其实就是函数在内存中的出栈入栈，DFS就是使用堆栈或者递归来实现，而类似层次遍历的BFS自然就可以使用队列来实现，这跟树的前序，中序，后序遍历（具体参考我之前的一篇博客）和层次遍历的思想是一样的。

       对于最短路径算法的Dijkstra、Floyd算法，Dijkstra算法是求从某个源点到其余各个顶点的最短路径（单源最短路径），时间复杂度为O()，主要思想为每次在未确定的顶点中选取最短的路径，并把最短路径的顶点设为确定值，然后再由源点经该点出发来松弛其他顶点的路径的值，重复以上步骤最后得到就是最短路径了。而Floyd算法针对的问题是求每对顶点之间的最短路径，相当于把Dijkstra算法执行了n遍（实际上并不是这样做），所以Floyd算法的时间复杂度为。但实际上Floyd算法核心代码就有五行，主要用公式来不断优化带权邻接矩阵，最后得到矩阵就是每对顶点之间的最短距离了。

       对于最小代价生成树的Prim、Kruskal算法，两种算法的主要核心思想是贪心算法。Prim算法是从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中，其实就是说在当前顶点集所可以辐射到的边中选择最小的一条边（需要判断该边是否已经在最小生成树中），其实就是一个排序问题，然后贪心选取最小值。Kruskal算法则是另外一种思维，选择从边开始，把所有的边按照权值先从小到大排列，接着按照顺序选取每条边（贪心思想），如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止，其实就是基于并查集的贪心算法。两种算法各有不同，Prim算法的时间复杂度为，n表示顶点数目，这跟它的初心还是蛮符合的，毕竟它是从顶点出发，可以从公式中看出Prim算法的时间复杂度与网络中的边无关，所以适合来求解边稠密的网的最小代价生成树。而Kruskal算法恰恰相反，它适合来求边稀疏的网的最小代价生成树，时间复杂度为，e表示网络中的边数。

2.show me the code

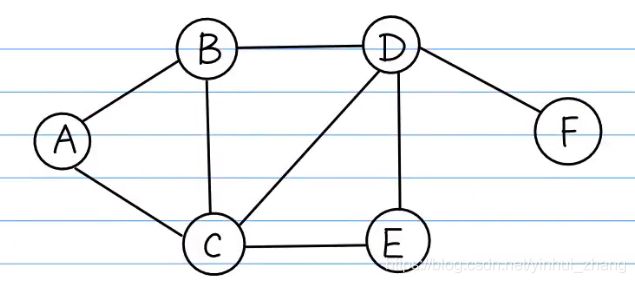
DFS、BFS

 

                                                        

graph = {
        'a' : ['b', 'c'],
        'b' : ['a', 'c', 'd'],
        'c' : ['a','b', 'd','e'],
        'd' : ['b' , 'c', 'e', 'f'],
        'e' : ['c', 'd'],
        'f' : ['d']
        }


def BFS(graph, s):
    queue = []
    queue.append(s)
    seen = set()
    seen.add(s)
    while len(queue) > 0:
        vertex = queue.pop(0)
        nodes = graph[vertex]
        for node in nodes:
            if node not in seen:
                queue.append(node)
                seen.add(node)
        print(vertex)
        
BFS(graph, 'a')


def DFS(graph, s):
    stack = []
    stack.append(s)
    seen = set()
    seen.add(s)
    while len(stack) > 0:
        vertex = stack.pop()
        nodes  = graph[vertex]
        for node in nodes:
            if node not in seen:
                stack.append(node)
                seen.add(node)
        print(vertex)
DFS(graph, 'a')


def DFS1(graph, s, queue=[]):
    queue.append(s)
    for i in graph[s]:
        if i not in queue:
            DFS1(graph, i, queue)
    return queue
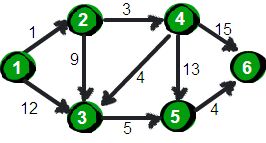
print(DFS1(graph, 'a'))

Dijkstra、Floyd算法

                                                               

inf = float('inf')
matrix_distance = [[0,1,12,inf,inf,inf],
                   [inf,0,9,3,inf,inf],
                   [inf,inf,0,inf,5,inf],
                   [inf,inf,4,0,13,15],
                   [inf,inf,inf,inf,0,4],
                   [inf,inf,inf,inf,inf,0]]

def dijkstra(matrix_distance, source_node):
    inf = float('inf')
    # init the source node distance to others
    dis = matrix_distance[source_node]
    node_nums = len(dis)
    
    flag = [0 for i in range(node_nums)]
    flag[source_node] = 1
    
    for i in range(node_nums-1):
        min = inf
        #find the min node from the source node
        for j in range(node_nums):
            if flag[j] == 0 and dis[j] < min:
                min = dis[j]
                u = j
        flag[u] = 1
        #update the dis 
        for v in range(node_nums):
            if flag[v] == 0 and matrix_distance[u][v] < inf:
                if dis[v] > dis[u] + matrix_distance[u][v]:
                    dis[v] = dis[u] + matrix_distance[u][v]                    
    
    return dis

print(dijkstra(matrix_distance, 1))


def Floyd(dis):
    #min (Dis(i,j) , Dis(i,k) + Dis(k,j) )
    nums_vertex = len(dis[0])
    for k in range(nums_vertex):
        for i in range(nums_vertex):
            for j in range(nums_vertex):
                if dis[i][j] > dis[i][k] + dis[k][j]:
                    dis[i][j] = dis[i][k] + dis[k][j]
    return dis

print(Floyd(matrix_distance))

Prim、Kruskal算法

"""
代码来源：https://github.com/qiwsir/algorithm/blob/master/kruskal_algorithm.md
        https://github.com/qiwsir/algorithm/blob/master/prim_algorithm.md
做了几个细节的小改动
"""


from collections import defaultdict
from heapq import *
    
def Prim(vertexs, edges, start_node):
    adjacent_vertex = defaultdict(list)
    for v1, v2, length in edges:
        adjacent_vertex[v1].append((length, v1, v2))
        adjacent_vertex[v2].append((length, v2, v1))
        
    mst = []
    closed = set(start_node)
    
    adjacent_vertexs_edges = adjacent_vertex[start_node]
    heapify(adjacent_vertexs_edges)

    while adjacent_vertexs_edges:
        w, v1, v2 = heappop(adjacent_vertexs_edges)
        if v2 not in closed:
            closed.add(v2)
            mst.append((v1, v2, w))
            
            for next_vertex in adjacent_vertex[v2]:
                if next_vertex[2] not in closed:
                    heappush(adjacent_vertexs_edges, next_vertex)
                    
    return mst
    
    
vertexs = list("ABCDEFG")
edges = [ ("A", "B", 7), ("A", "D", 5),
          ("B", "C", 8), ("B", "D", 9), 
          ("B", "E", 7), ("C", "E", 5),
          ("D", "E", 15), ("D", "F", 6),
          ("E", "F", 8), ("E", "G", 9),
          ("F", "G", 11)]

print('prim:', Prim(vertexs, edges, 'A'))

#****************************************************


node = dict()
rank = dict()

def make_set(point):
    node[point] = point
    rank[point] = 0
    
def find(point):
    if node[point] != point:
        node[point] = find(node[point])
    return node[point]

def merge(point1, point2):
    root1 = find(point1)
    root2 = find(point2)
    if root1 != root2:
        if rank[root1] > rank[root2]:
            node[root2] = root1
        else:
            node[root1] = root2
            if rank[root1] == rank[root2] : rank[root2] += 1
            
            
def Kruskal(graph):
    for vertice in graph['vertices']:
        make_set(vertice)
    
    mst = set()
    
    edges = list(graph['edges'])
    edges.sort()
    for edge in edges:
        weight, v1, v2 = edge
        if find(v1) != find(v2):
            merge(v1 , v2)
            mst.add(edge)
    return mst

graph = {
    'vertices': ['A', 'B', 'C', 'D'],
    'edges': set([
        (1, 'A', 'B'),
        (5, 'A', 'C'),
        (3, 'A', 'D'),
        (4, 'B', 'C'),
        (2, 'B', 'D'),
        (1, 'C', 'D'),
        ])
    }

print(Kruskal(graph))

reference

1.算法(第4版) [美] Robert Sedgewick，[美] Kevin Wayne 著，谢路云 译

2.图解Dijkstra算法和Floyd算法  （看图就好）

3.Dijkstra 最短路算法

4.图解 Prim、Kruskal算法

5.最小生成树之Kruskal算法

6.并查集