算法导论第13(十三)章红黑树
红黑树的定义：红黑树是一种较为“平衡的”二叉查找树，其每个结点上增加了一个储存颜色的位置，可以是红也可以是黑色的，并且有父亲结点。基本操作时间为O(lgn).
红黑树的性质：1)每个结点或是红的，或是黑的。2)根结点是黑的。 3)每个叶结点(NIL)是黑的。 4)若一个结点是红的，则它的两个儿子都是黑的。5)对每个结点，从该结点到其子孙结点的所有路径上的黑色结点数目相同。
黑高度：从某个结点x出发(不包括该结点)到达一个叶结点的任意一条路径上，黑色结点的个数称为该结点x的黑高度，用bh(x)表示。
引理13.1 一棵有n个内结点的红黑树的高度至多为2lg(n+1).
练习：
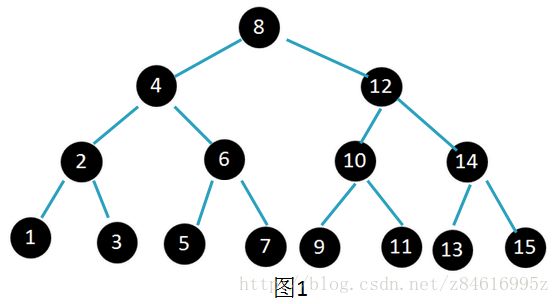
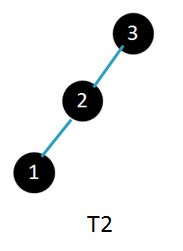
13.1-1 使用图13-1a的格式，画出在关键字集合{1,2,....,15}上高度为3的完全二叉查找树。以三种不同方式，向图中加入NIL叶结点并对各结点着色，使所得的红黑树的黑高度分别为2,3,4.
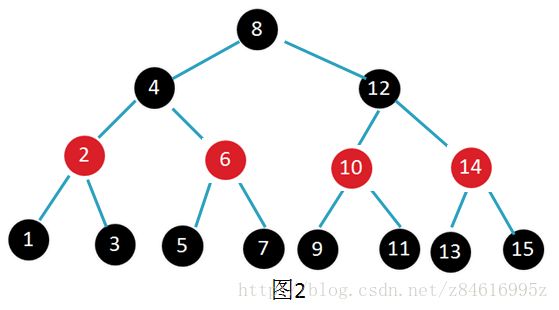
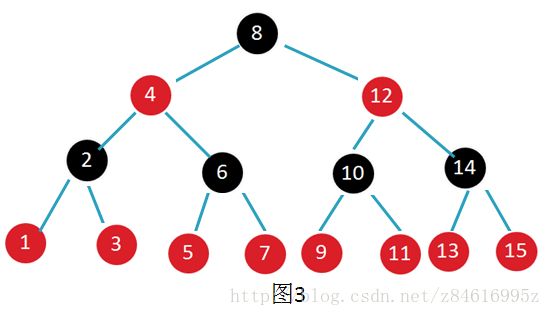
图1表示黑度为4的红黑树，图2表示黑度为3的红黑树，图3表示黑度为2的红黑树。
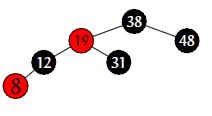
13.1-2对图13-1中的红黑树，画出调用TREE-INSERT插入关键字36后的结果。结果插入的结点被标为红色，所得的树是否还是一棵红黑树？如果该结点被标为黑色呢？
标为红色后，不是红黑树，不符合性质4. 标为黑色后，不是红黑树，不符合性质5.第3节学习插入函数后，可以知道每插入一个红色结点，可以通过调整使之成为一棵红黑树。
13.1-3 定义松弛红黑树为满足红黑性质1,3,4,5的二叉查找树。换言之，根部可以是红色或是黑色。考虑一棵根是红色的松弛红黑树T。如果将T的根部标为黑色而其他都不变，则所得到的是否还是一棵红黑树？
是。
13.1-4假设将一棵红黑树的每一个红结点“吸收”到它的黑色父结点中，来让红结点的子女变成黑色父结点的子女(忽略关键字的变化)。当一个黑结点的所有红色子女都被吸收后，其可能的度是多少？此结果树的叶子深度怎么样？
度为2时，是左右孩子结点已经都是黑色。度为3时，左或者右孩子结点是红色。 度为4时，左右孩子结点都是红色。 结果树叶子深度都相同。
以下13.1-5~7 都用到了红黑树一个特别的结构，那就是从根结点开始，一层黑一层红，颜色交替，构成了一棵拥有红色结点最多的红黑树。
13.1-5 证明：在一棵红黑树中，从某结点x到其后代叶结点的所有简单路径中，最长的一条是最短一条的至多两倍。
最短：此路径上全是黑色结点。最长：此路径上红黑结点交替出现(红色结点数目=黑色结点数目)，又因为不管到最长路径还是到最短路径，黑高(黑色结点数目)都相等。最长：最短=(红+黑)：黑=2:1:由此得出论点。
13.1-6 在一棵黑高度为k的红黑树中，内结点最多可能有多少个？最少可能有多少个？
根据引理13.1 至少包含2^k-1个内部结点。至多包含2^(2k)-1个内部结点。(最多就是红黑结点交替出现的情况)
13.1-7 请描述出一棵在n个关键字上构造出来的红黑树，使其中红的内部结点数与黑的内部结点数比值最大。这个比值是多少？具有最小可能比例的树又是怎么样？此比值是多少？
最小可能比值就是所有结点都是黑色，比值为0。 最大可能是红黑结点交替出现，并且最底层是全部是红色结点，比值是2:1.
13.2 旋转
旋转分为：左旋和右旋。
左旋：在某个结点x做左旋时，它的右孩子非空。 右旋：在某个结点x做右旋时，它的左孩子非空。
//两个结点间是由两个指针连接成的 可以说x的孩子结点指向B，同时也是B的父亲结点指向x 由于有父亲结点属性的存在，所以是双向连接
左旋代码如下：
struct Tree*root=NULL;
void LEFT_ROTATE(struct Tree*T,struct Tree*x)
{//左旋转：分三个步骤①②③来叙述旋转代码的。
struct Tree*y=x->right;//设置y结点。
x->right=y->left;//本行代码以及下面的if结构表达的是“y的左孩子成为x的右孩子”。①
if(y!=NULL&&y->left!=NULL)
{
y->left->parent=x;
}
y->parent=x->parent;//本行代码以及下面的if-else结构表达的过程是“y成为该子树新的根”。②
if(x->parent==NULL)
{
root=y;
}
else if(x==x->parent->left)
{
x->parent->left=y;
}
else x->parent->right=y;
y->left=x;//本行代码以及下面一行都表达了“x成为y的左孩子”。③
x->parent=y;
}13.2-1 写出RIGHT-ROTATE的伪代码。
只需将书中的代码中的right变为left,而left变为right即可。
13.2-2 证明：在一棵有n个结点的二叉查找树中，刚好有n-1种可能的旋转。
因为n个结点有n-1条边，每条边都可以(左或右)旋转，所以有n-1种可能的旋转。
13.2-3设在图13-2的左边一棵树中，a,b,c分别为子树α,β,γ中的任意结点。如果将结点x左旋，则a,b,c深度如何变化？
α上升1层,β不变，γ下降1层。
13.2-4 证明：任何一棵含n个结点的二叉查找树，可以通过O(n)次旋转，转变为另一棵含n个结点的二叉查找树。
每次右(左)旋转，都会使最右(左)链上多一个结点，经过任意n-1次右(左)旋转,任意右(左)总会变成一个单链表。所以任意二叉查找树都能经过O(n)次旋转转换成任意二叉查找树。
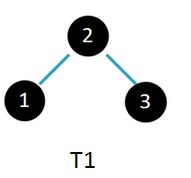
13.2-5 如果能够使用一系列的RIGHT-ROTATE调用来把一个二叉查找树T1变为二叉查找树T2，则说T1可以右转成T2。请给出一个两棵树的例子，其中T1不能右转成T2.然后证明如果T1可以右转成T2，则它可以使用O(n^2)次RIGHT-ROTATE调用来右转。
第二问不太懂。
13.3插入
红黑树的插入函数只需要把第12章的二叉查找树稍微修改一下即可实现，但是由于插入时需要保持红黑树性质，所以我们引入RB_INSERT_FIXUP函数，这才是插入函数关键
代码如下：
void RB_INSERT_INSERT_FIXUP(struct Tree*T,struct Tree*z)
{
while (z->parent->color==RED)
{
if (z->parent==z->parent->parent->left)
{
struct Tree*y=z->parent->parent->right;//叔结点
if (y->color==RED)//情况一：叔结点为红色
{//给p1,y,p2着色以保持性质5。并且解决了z的父结点和z都是红色结点问题
z->parent->color=BLACK;
y->color=BLACK;
z->parent->parent->color=RED;
z=z->parent->parent;//把z的祖父结点当成新结点z进入下一次循环
}
else
{
if (z==z->parent->right)//情况二：检查z是否是一个右孩子且叔结点为黑色，前提是p1结点不是叶子结点
{//使用一个左旋让情况2转变为情况3
z=z->parent;
LEFT_ROTATE(T,z);//由于进入if语句后可知旋转结点不可能是叶子结点，这样就不用判断z是否是叶子结点了。
}
z->parent->color=BLACK;//情况三：是z是一个左孩子且叔结点为黑色，改变z的父和祖父结点颜色并做一次右旋，以保持性质5
z->parent->parent->color=RED;
RIGHT_ROTATE(T,z->parent->parent);//z的祖父结点不会是叶子结点(由13.3-4可知)，所以不用在右旋前做判断。
}
}
else//下面else分支类似于上面,注意到else分支的情况2和情况3所做旋转正好是if分支情况的逆。
{
struct Tree*y=z->parent->parent->left;
if (y->color==RED)
{
z->parent->color=BLACK;
y->color=BLACK;
z->parent->parent->color=RED;
z=z->parent->parent;
}
else
{
if (z==z->parent->left)
{
z=z->parent;
RIGHT_ROTATE(T,z);
}
z->parent->color=BLACK;
z->parent->parent->color=RED;
LEFT_ROTATE(T,z->parent->parent);
}
}
}
root->color=BLACK;//最后给根结点着为黑色。
}
void RB_INSERT(struct Tree*T,struct Tree*z)
{
struct Tree*y=nil;
struct Tree*x=root;
while (x!=nil)
{
y=x;
if (z->keykey)
{
x=x->left;
}
else x=x->right;
}
z->parent=y;
if (y==nil)
{
root=z;
}
else if(z->keykey)
{
y->left=z;
}
else y->right=z;
z->left=nil;//给插入结点左右孩子赋值为空。
z->right=nil;
z->color=RED;//给插入结点着为红色。
RB_INSERT_INSERT_FIXUP(T,z);
}
练习：
13.3-1在RB_INSERT的第16行中，假设新插入的结点z是红的。注意如果将z着为黑色，则红黑树性质4就不会被破坏。那么我们为什么没有选择将z着为黑色呢？
如果z着为黑色，那么性质5会被破坏，红黑树调整起来会更复杂。
13.3-2在将关键字48,38,31,12,19,8插入一棵初始为空的红黑树中之后，结果树是什么样子？
13.3-3假设图13-5和图13-6中子树α，β，γ，δ和ε的黑高度都是k.标上各个节点的黑高度，以验证图中所示的各种转换能保持性质5.
各个结点的黑高如下图：
由图可以看出经过以上所有图中的子树黑高都是k+2.所以保持性质5.
13.3-4 Teach教授担心RB_INSERT_FIXUP可能将叶子结点设置为RED。这时当z为根时，第1行的测试就不会让循环结束。通过证明RB_INSERT-FIXUP永远不会将叶子结点设置为RED，来说明这位教授担心是没有必要的。
如果结点z是叶子结点的话，那么z.p必然是根节点，根据循环不变式b部分可知z.p是黑色的，那么循环自动结束，所以也就遍历不到z.p.p这个叶子结点了。特别要注意的是在case2时，我们把z=z.p让z上升1层，但是通过旋转又让z下降一层，这样z.p.p的地位不变，所以没有问题。
13.3-5 考虑用RB_INSERT插入n个结点而成的一棵红黑树。证明：如果n>1，则该树至少有一个红结点。
最坏情况是假设前n-1个插入结点后都为黑色，那么第n个结点插入后，由于开始设置为红色，满足红黑树性质，所以此结点颜色不会由于RB_INSERT_FIXUP调整而改变。
13.3-6说明如果红黑树的表示中不提供父指针的话，应当如何有效地实现RB_INSERT.
13.3-6不带父结点的红黑树
13.3-6不带父结点的红黑树
13.4删除
删除操作运行时间是O(lgn).并且比插入操作复杂。
代码如下：
void RB_DELETE_FIXUP(struct Tree*x)
{
struct Tree*w=NULL;//w是x的兄弟结点
while (x!=root&&x->color==BLACK)//如果x是黑色并且不是根结点，才进行循环。
{//x是一个具有双重颜色的结点，调整的目的是把x的黑色属性向上移动。
if (x==x->parent->left)
{
w=x->parent->right;
if (w->color==RED)//情况一：x的兄弟结点w是红色的。
{//改变w和x.p的颜色+一次旋转使其变为情况二，三，四。
w->color=BLACK;
x->parent->color=RED;
LEFT_ROTATE(x->parent);
w=x->parent->right;
}
if (w->left->color==BLACK&&w->right->color==BLACK)//情况二：x的兄弟结点w是黑色的，而且w的两个子节点都是黑色。
{
w->color=RED;//从x和w上去掉一重黑色。x还是黑色，而w变为红色。
x=x->parent;//x结点向上移动成为新的待调整结点。
}
else
{
if (w->right->color==BLACK)//情况三：x的兄弟结点w是黑色的，w的左孩子是红色的，w的右孩子是黑色的。
{//交换w和w.left的颜色+旋转使其转变为情况四。
w->left->color=BLACK;
w->color=RED;
RIGHT_ROTATE(w);
w=x->parent->right;
}
w->color=x->parent->color;//以下是情况四：x的兄弟结点w是黑色的，且w的右孩子是红色的。
x->parent->color=BLACK;//置x.p和w.right为黑色+旋转使其去掉x的额外黑色。
w->right->color=BLACK;
LEFT_ROTATE(x->parent);
x=root;//x成为根结点，结束循环。
}
}
else//以下和上面的if分支类似，不做累述。
{
w=x->parent->left;
if (w->color==RED)
{
w->color=BLACK;
x->parent->color=RED;
RIGHT_ROTATE(x->parent);
w=x->parent->left;
}
if (w->left->color==BLACK&&w->right->color==BLACK)
{
w->color=RED;
x=x->parent;
}
else
{
if (w->left->color==BLACK)
{
w->right->color=BLACK;
w->color=RED;
LEFT_ROTATE(w);
w=x->parent->left;
}
w->color=x->parent->color;
x->parent->color=BLACK;
w->left->color=BLACK;
RIGHT_ROTATE(x->parent);
x=root;
}
}
}x->color=BLACK;
}
void RB_DELETE(struct Tree*z)
{
struct Tree*y=z,*x;//y为待删除或待移动结点
int y_original_color=y->color;//保存y的原始颜色，为做最后的调整做准备。
if (z->left==nil)
{
x=z->right;//x指向y的唯一子结点或者是叶子结点，保存x的踪迹使其移动到y的原始位置上
RB_TRANSPLANT(z,z->right);//把以z.right为根的子树替换以z为根的子树。
}
else if (z->right==nil)
{
x=z->left;//x指向y的唯一子结点或者是叶子结点，保存x的踪迹使其移动到y的原始位置上
RB_TRANSPLANT(z,z->left);//把以z.left为根的子树替换以z为根的子树。
}
else
{
y=ITERATIVE_TREE_MINIMUM(z->right);//找到z.right的后继。
y_original_color=y->color;//y的新的原始结点被重置。
x=y->right;//x指向y的唯一子结点或者是叶子结点，保存x的踪迹使其移动到y的原始位置上
if (y->parent==z)
{
x->parent=y;//由于z的父结点是要删除的结点，所以不能指向它，于是指向y
}
else
{
RB_TRANSPLANT(y,y->right);//把以y.right为根的子树替换以y为根的子树。
y->right=z->right;
y->right->parent=y;
}
RB_TRANSPLANT(z,y);//把以y为根的子树替换以z为根的子树。
y->left=z->left;
y->left->parent=y;
y->color=z->color;//把已经删除的结点颜色赋值给y，保证了y以上的树结构红黑性质不变。
}
if(y_original_color==BLACK) //y的原始颜色为黑色，说明需要调整红黑颜色。
RB_DELETE_FIXUP(x);
}
既然删除代码也已经给出，那么下面是
第13章红黑树涉及的所有函数代码如下：
#include
using namespace std;
#define BLACK 0
#define RED 1
#define Nil -1
#define LEN sizeof(struct Tree)
struct Tree
{
struct Tree*left;
struct Tree*right;
struct Tree*parent;
int key;
int color;
};
struct Tree*root=NULL;
struct Tree*nil=NULL;
void LEFT_ROTATE(struct Tree*x)
{//左旋转：分三个步骤①②③来叙述旋转代码的。
struct Tree*y=x->right;//设置y结点。
x->right=y->left;//本行代码以及下面的if结构表达的是“y的左孩子成为x的右孩子”。①
if(y->left!=nil)
{
y->left->parent=x;
}
y->parent=x->parent;//本行代码以及下面的if-else结构表达的过程是“y成为该子树新的根”。②
if(x->parent==nil)
{
root=y;
}
else if(x==x->parent->left)
{
x->parent->left=y;
}
else x->parent->right=y;
y->left=x;//本行代码以及下面一行都表达了“x成为y的左孩子”。③
x->parent=y;
}
void RIGHT_ROTATE(struct Tree*x)
{//右旋转：分三个步骤①②③来叙述旋转代码的。
struct Tree*y=x->left;//设置y结点。
x->left=y->right;//本行代码以及下面的if结构表达的是“y的左孩子成为x的右孩子”。①
if(y->right!=nil)
{
y->right->parent=x;
}
y->parent=x->parent;//本行代码以及下面的if-else结构表达的过程是“y成为该子树新的根”。②
if(x->parent==nil)
{
root=y;
}
else if(x==x->parent->right)
{
x->parent->right=y;
}
else x->parent->left=y;
y->right=x;//本行代码以及下面一行都表达了“x成为y的左孩子”。③
x->parent=y;
}
void RB_INSERT_INSERT_FIXUP(struct Tree*z)
{
while (z->parent->color==RED)
{
if (z->parent==z->parent->parent->left)
{
struct Tree*y=z->parent->parent->right;//叔结点
if (y->color==RED)//情况一：叔结点为红色
{//给p1,y,p2着色以保持性质5。并且解决了z的父结点和z都是红色结点问题
z->parent->color=BLACK;
y->color=BLACK;
z->parent->parent->color=RED;
z=z->parent->parent;//把z的祖父结点当成新结点z进入下一次循环
}
else
{
if (z==z->parent->right)//情况二：检查z是否是一个右孩子且叔结点为黑色，前提是p1结点不是叶子结点
{//使用一个左旋让情况2转变为情况3
z=z->parent;
LEFT_ROTATE(z);//由于进入if语句后可知旋转结点不可能是叶子结点，这样就不用判断z是否是叶子结点了。
}
z->parent->color=BLACK;//情况三：是z是一个左孩子且叔结点为黑色，改变z的父和祖父结点颜色并做一次右旋，以保持性质5
z->parent->parent->color=RED;
RIGHT_ROTATE(z->parent->parent);//由于p2可能是叶子结点，所以最好还是用一个if判断
}
}
else//下面else分支类似于上面,注意到else分支的情况2和情况3所做旋转正好是if分支情况的逆。
{
struct Tree*y=z->parent->parent->left;
if (y->color==RED)
{
z->parent->color=BLACK;
y->color=BLACK;
z->parent->parent->color=RED;
z=z->parent->parent;
}
else
{
if (z==z->parent->left)
{
z=z->parent;
RIGHT_ROTATE(z);
}
z->parent->color=BLACK;
z->parent->parent->color=RED;
LEFT_ROTATE(z->parent->parent);
}
}
}
root->color=BLACK;//最后给根结点着为黑色。
}
void RB_INSERT(struct Tree*z)
{
struct Tree*y=nil;
struct Tree*x=root;
while (x!=nil)
{
y=x;
if (z->keykey)
{
x=x->left;
}
else x=x->right;
}
z->parent=y;
if (y==nil)
{
root=z;
}
else if(z->keykey)
{
y->left=z;
}
else y->right=z;
z->left=nil;//给插入结点左右孩子赋值为空。
z->right=nil;
z->color=RED;//给插入结点着为红色。
RB_INSERT_INSERT_FIXUP(z);
}
void RB_TRANSPLANT(struct Tree*u,struct Tree*v)
{
if (u->parent==nil)
root=v;
else if(u==u->parent->left)
u->parent->left=v;
else u->parent->right=v;
v->parent=u->parent;
}
//非递归版本的查找二叉查找树的最小值
struct Tree*ITERATIVE_TREE_MINIMUM(struct Tree*x)
{
while (x->left!=nil)
{
x=x->left;
}
return x;
}
//非递归版本的二叉查找树查找函数
struct Tree*ITERATIVE_TREE_SEARCH(struct Tree*x,int k)
{
while (x!=nil&&k!=x->key)
{
if (kkey)
{
x=x->left;
}
else x=x->right;
}
return x;
}
void RB_DELETE_FIXUP(struct Tree*x)
{
struct Tree*w=NULL;//w是x的兄弟结点
while (x!=root&&x->color==BLACK)//如果x是黑色并且不是根结点，才进行循环。
{//x是一个具有双重颜色的结点，调整的目的是把x的黑色属性向上移动。
if (x==x->parent->left)
{
w=x->parent->right;
if (w->color==RED)//情况一：x的兄弟结点w是红色的。
{//改变w和x.p的颜色+一次旋转使其变为情况二，三，四。
w->color=BLACK;
x->parent->color=RED;
LEFT_ROTATE(x->parent);
w=x->parent->right;
}
if (w->left->color==BLACK&&w->right->color==BLACK)//情况二：x的兄弟结点w是黑色的，而且w的两个子节点都是黑色。
{
w->color=RED;//从x和w上去掉一重黑色。x还是黑色，而w变为红色。
x=x->parent;//x结点向上移动成为新的待调整结点。
}
else
{
if (w->right->color==BLACK)//情况三：x的兄弟结点w是黑色的，w的左孩子是红色的，w的右孩子是黑色的。
{//交换w和w.left的颜色+旋转使其转变为情况四。
w->left->color=BLACK;
w->color=RED;
RIGHT_ROTATE(w);
w=x->parent->right;
}
w->color=x->parent->color;//以下是情况四：x的兄弟结点w是黑色的，且w的右孩子是红色的。
x->parent->color=BLACK;//置x.p和w.right为黑色+旋转使其去掉x的额外黑色。
w->right->color=BLACK;
LEFT_ROTATE(x->parent);
x=root;//x成为根结点，结束循环。
}
}
else//以下和上面的if分支类似，不做累述。
{
w=x->parent->left;
if (w->color==RED)
{
w->color=BLACK;
x->parent->color=RED;
RIGHT_ROTATE(x->parent);
w=x->parent->left;
}
if (w->left->color==BLACK&&w->right->color==BLACK)
{
w->color=RED;
x=x->parent;
}
else
{
if (w->left->color==BLACK)
{
w->right->color=BLACK;
w->color=RED;
LEFT_ROTATE(w);
w=x->parent->left;
}
w->color=x->parent->color;
x->parent->color=BLACK;
w->left->color=BLACK;
RIGHT_ROTATE(x->parent);
x=root;
}
}
}x->color=BLACK;
}
void RB_DELETE(struct Tree*z)
{
struct Tree*y=z,*x;//y为待删除或待移动结点
int y_original_color=y->color;//保存y的原始颜色，为做最后的调整做准备。
if (z->left==nil)
{
x=z->right;//x指向y的唯一子结点或者是叶子结点，保存x的踪迹使其移动到y的原始位置上
RB_TRANSPLANT(z,z->right);//把以z.right为根的子树替换以z为根的子树。
}
else if (z->right==nil)
{
x=z->left;//x指向y的唯一子结点或者是叶子结点，保存x的踪迹使其移动到y的原始位置上
RB_TRANSPLANT(z,z->left);//把以z.left为根的子树替换以z为根的子树。
}
else
{
y=ITERATIVE_TREE_MINIMUM(z->right);//找到z.right的后继。
y_original_color=y->color;//y的新的原始结点被重置。
x=y->right;//x指向y的唯一子结点或者是叶子结点，保存x的踪迹使其移动到y的原始位置上
if (y->parent==z)
{
x->parent=y;//由于z的父结点是要删除的结点，所以不能指向它，于是指向y
}
else
{
RB_TRANSPLANT(y,y->right);//把以y.right为根的子树替换以y为根的子树。
y->right=z->right;
y->right->parent=y;
}
RB_TRANSPLANT(z,y);//把以y为根的子树替换以z为根的子树。
y->left=z->left;
y->left->parent=y;
y->color=z->color;//把已经删除的结点颜色赋值给y，保证了y以上的树结构红黑性质不变。
}
if(y_original_color==BLACK) //y的原始颜色为黑色，说明需要调整红黑颜色。
RB_DELETE_FIXUP(x);
}
//中序遍历
void InOderTraverse(struct Tree *p)
{
if (p!=nil)
{
InOderTraverse(p->left);
cout<key<<" "<color<<" "<right);
}
}
void main()
{
int array1[6] = {41, 38, 31, 12, 19, 8};
nil=new struct Tree[LEN];
nil->key=Nil;nil->color=BLACK;
root=nil;
int i=0;
struct Tree*ROOT=new struct Tree[LEN];
ROOT->key=array1[i++];
RB_INSERT(ROOT);
root=ROOT;
while (i!=6)
{
struct Tree*z=new struct Tree[LEN];
z->key=array1[i];
RB_INSERT(z);
i++;
}
InOderTraverse(root);
cout< 13.4-1 在执行RB_DELETE-FIXUP之后，证明：树根一定是黑色的。
若x为根结点，则不进入循环，直接给根x着为黑色。
若x非根且x为红结点，则不进入循环，也就不对除x以外的任何结点给变颜色，所以根结点颜色也一样不变。
若x非根且x为黑结点，则进入循环，注意到书中第6行，x的父结点被设置为红色，此时如果x父结点为根，那么在case1完成后会进入case2，3，4。进入case2时，x的父结点为新的x结点并且为红色循环自动结束，并在最后给新x着为黑色。若进入case34，注意到代码第18行x父结点被着为黑色，若x父节点为根，那么这里已经将其染黑。若开始不进入case1直接case2，那么x的父结点被更新为新x结点，新x结点为红色的话，循环退出，并且最后把新x结点着为黑色。若开始直接进入case34，那么x父结点即使为根，也在第18行被染为黑色，并且case4过后循环退出。总之根一定是黑色。
13.4-2在RB_DELETE中，如果x和x.p都是红色的。证明：可以通过调用RB_DELETE_FIXUP(T,x)来恢复性质4.
x和x.p都为红色，那么不进入循环，直接最后把x着为黑色以恢复性质4.。
13.4-3在练习13.3-3中，将关键字41,38,31,12,19,8连续插入一棵初始的空树中，从而得到一棵红黑树。请给出从该树中连续删除关键字8,12,19,31,38,41后的红黑树。
用上面完整红黑树代码可以实现本题要求。
13.4-4在RB_DELETE_FIXUP代码的哪些行中，可能会检查或修改哨兵T.nil?
书中代码第1,5,4,9,12,13,19行。
13.4-5在图13-7的每种情况中，给出所示子树的根结点至每棵子树α，β，......,ξ之间的黑结点个数，并验证它们在转换之后保持不变。当一个结点的color属性为c或c'时，在计数中用记号count(c)或count(c')来表示。
图a与图b在书中已经给出答案。图c子树α，β，......,ξ转换前后黑结点个数都是count(c)+2。图d α与β黑结点数count(c)+2. γ与δ黑结点数count(c)+count(c')+1.其他子树黑结点1+count(c).
13.4-6 Skelton和Baron教授担心在RB_DELETE_FIXUP的情况1开始时，结点x.p可能不是黑色的。如果这两位教授是对的，则第5-6行就是错的。证明：x.p在情况1开始时必是黑色的，从而说明这两位教授没有必要担心。
若x.p不是黑色的，那么w结点必然不是红色的。也就不会执行5-6行代码。
13.4-7 假设用RB_INSERT将一个结点x插入一棵红黑树，紧接着又用RB_DELETE将它从树中删除。结果的红黑树与初始红黑树是否一样？证明你的答案。
不一样。可以用上面所给完整代码进行验证，这里就略过。
思考题
13-1 持久动态集合
思考题13-1
13-2 红黑树的连接操作
13-2 红黑树的连接操作
思考题13-2
13-3 AVL树
思考题13-3
13-4 Treap树
思考题13-4