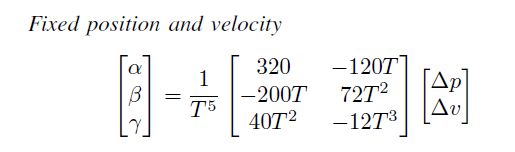庞特里亚金最小值原理求解能耗最小化的时间最优OBVP问题

本文依据论文A computationally efficient motion primitive for quadrocopter trajectory generation中所述的方法，整理出其中对OBVP问题的求解方法。所谓的OBVP即为optimal boundary value problem。

OBVP是特殊的BVP问题，最简单的BVP问题就是state sampled lattice planning,这其实也是一种lattice planner方法。常见的例子比如：给定初始位置和终点位置，求解多阶曲线方程。

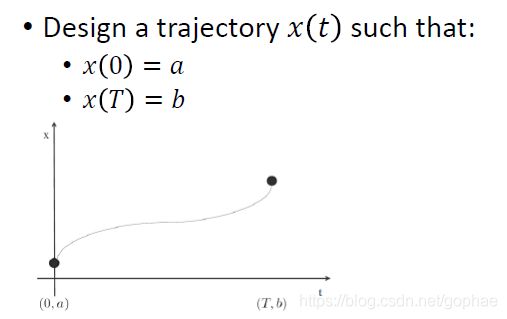
如果这条曲线是个五阶多项式：

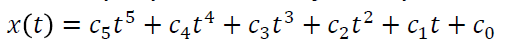
给定初始位置和终点位置a,b，则系数求解为：

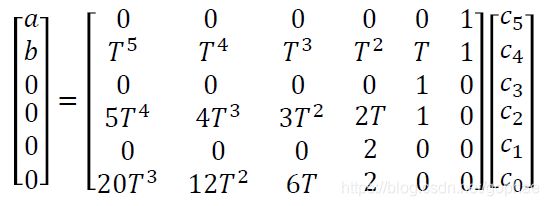
现在讨论OBVP方法，我们给定初始位置，和重点位置的，再给定一个objective function, 比如我们论文中描述的，objective function只考虑jerk的平方。那么问题的状态和位置速度加速度相关，系统的输入为jerk = u, 状态空间即为速度，加速度，jerk的函数，总结如下：

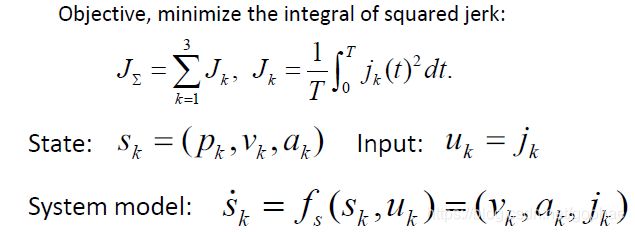
对于这个问题，我们用庞特里亚金最小值原理求解：
最小值原理的基本内容：

先写出hamiltonian，这个g就是objective function中的transition cost, f 就是状态方程(上面的system model):

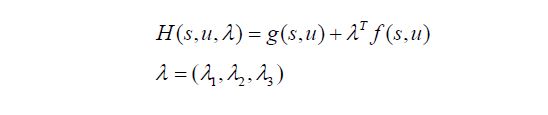
那么在本问题中，对应的g就是 j^2, f就是三个系统状态 a, v, j.写出如下的表达式：

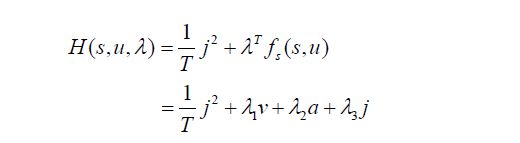
根据上面的最小值原理基本内容：

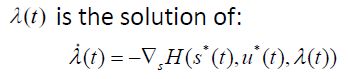
我们计算lamda梯度(H分别对 a,v,j求导数)：

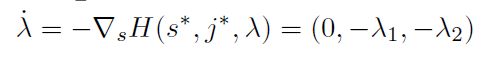
然后积分获得lamda表达式(这里对系数稍作了处理，是为了后面计算结果好看)：

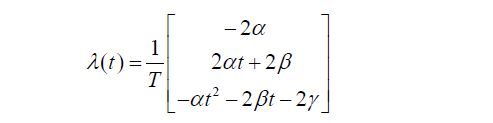
继续看最小值原理：

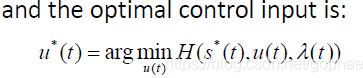
我们的lamda已经求解出来了，而且其中s是打星号（optimal）的，所以在H里面：

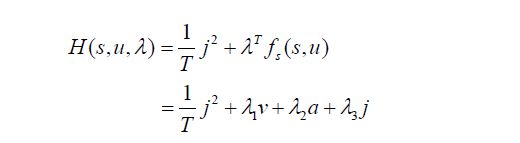
v和a都是知道一定是最优解的，那么只要算一下j是多少就行了。求一下一阶导数就能算出j的值，再带入H的表达式，得到：

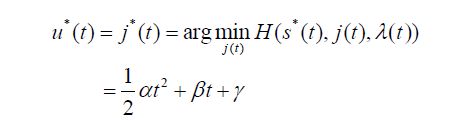
对u做一次积分得到a, 在积分得到V，在积分得到p:

整理一下：

这里算逆矩阵可以自己验算一下：

%%
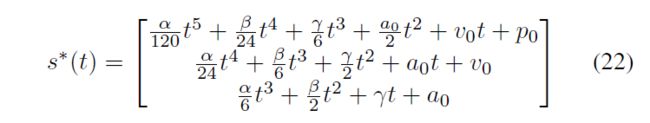
clear all; close all;
syms delta_p delta_v delta_a
syms T

Variants = [1/120*T^5 1/24*T^4 1/6*T^3;1/24*T^4 1/6*T^3 1/2*T^2;...
    1/6*T^3 1/2*T^2 T];

inv_Variants = inv(Variants)

结果没问题：

inv_Variants =
 
[  720/T^5, -360/T^4,  60/T^3]
[ -360/T^4,  168/T^3, -24/T^2]
[   60/T^3,  -24/T^2,     3/T]

然后得到alpha, beta, gamma后，带入objective function，

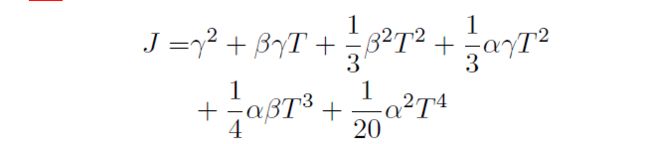
具体推导如下：

对cost function求一阶导数就知道T在什么时候可以取到minimum cost了，这里很有趣，objective function只和T相关。这也就是我们所谓的最小时间问题。

最后，还有其他终点的情况也要讨论一下，比如刚才的问题限制了终点的p,v,a，那么如果放开a的限制该如何求解。这里用到边界条件：

另外两个条件依旧不变，具体推导如下：

验证一下结果：

clear all; close all;
syms delta_p delta_v delta_a
syms T

Variants_2 = [1/120*T^5 1/24*T^4 1/6*T^3;1/24*T^4 1/6*T^3 1/2*T^2;...
    1/2*T^2 - T T-2 1 - 2/T];

inv_Variants_2 = inv(Variants_2)

结果如下：

inv_Variants_2 =
 
[  320/T^5, -120/T^4, -20/(3*(- T^2 + 2*T))]
[ -200/T^4,   72/T^3,        -8/(3*(T - 2))]
[   40/T^3,  -12/T^2,         T/(3*(T - 2))]

最后一项是0就不要管它了，所以解出表达式为：

其他的情况就不一一证明了：