蚁群算法（ACO）任务序列规划
本文为用蚁群算法做AUV导航中全局任务序列规划所做的笔记，仅供参考。全局任务序列规划就是，将很大的环境用离散的任务点填充，在全局规划出的任务序列点之间进行实时的局部规划。本文使用蚁群算法对任务序列进行优化。
——————————————首先学习一下蚁群算法——————————————-
1 ACO算法简介
按照百度百科的说法。蚁群算法，英文名为Ant Colony Optimization，是一种用来在图中寻找优化路径的机率型算法。蚁群算法是一种模拟进化算法。各个蚂蚁在没有事先告诉它们食物在什么地方的前提下开始寻找食物，当一只找到食物之后，它会向环境中释放一种挥发性分泌物（Pheromore，信息素），该物质随着时间的推移会逐渐挥发消失，信息素浓度的大小表征路径的远近，信息素会吸引其他更多的蚂蚁过来，这样越来越多的蚂蚁会找到食物。另外，蚂蚁的运动也会加入一定的随机因子，这样如果找到更近的路径的话，就会有更多的蚂蚁被吸引过来。最后，经过一段时间的运行之后，就会出现一条最短的路径被大多数蚂蚁重复着。
蚁群优化算法长用来求复杂离散优化问题的较好解。协作是该算法的一个关键设计组件，即将计算资源合理地分配到蚁群上，蚁群中蚂蚁之间间接通信。
1.1 假设
1）人造蚂蚁在离散的世界，总是从一个离散状态到另一个离散状态；
2）人造蚂蚁有一个内在（internal）的状态，这种状态包括对自身之前运动的记忆；
3）人造蚂蚁沉积的信息素总量和过去该位置通过的蚂蚁总数量有关，成正比；
4）人造蚂蚁释放信息素的时间依赖于问题，并不反映真实的蚂蚁行为；比如，大多数情况下，人工蚁群仅在生成一个解之后更新信息素沉积；
1.2 ACO算法路径规划
ACO算法在寻找最优路径方面（在图中）。首先初始化一张图（图有节点和边），在matlab里面可以用一个方阵来表示边，信息素是分布在边上的，所以信息素矩阵也可以用一个方阵表示；在一次进化（迭代）中，每只蚂蚁从起点开始按照ACO算法策略运动，这种策略是首先确定候选节点的概率，概率用下式计算
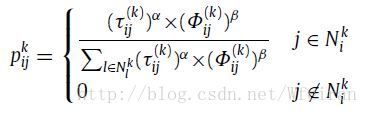
式中，第一项
表示边i-j之间的信息素浓度，
表示边i-j之间的启发因子，可以使用边长的倒数作为启发因子。根据上式，就可以计算出蚂蚁选择各个待选节点的概率。计算出概率之后，再计算累加概率，用轮盘赌策略选择下一节点。在一次进化（迭代）完成之后，每只蚂蚁不管有没有到达终点，都完成了它的本次旅程，在这些旅程路径中选择出符合条件的路径点序列（如必须到达终点，边不能重复等），用路径点序列的代价值作为分母来确定信息素增量。最后，在一次迭代完成之后，还要对所有边上的信息素整体减少，来模拟信息素的挥发。
——————————————使用蚁群算法进行任务序列规划——————————————-
2 AUV任务序列规划
海洋环境是建模成路径点组成的任务点网络图，需执行的任务稀疏地安排在网络图中的边上，任务优先级也在AUV开始执行任务之前以权重值的形式指定。有任务的边优先级权重值设置为大于1的数，没有任务的边优先级权重值设置为1。AUV要在有限的时间内，从任务起点开始，完成最大数量的高优先级任务，并在结束时到达任务终止点。因为AUV能量和任务总时间的限制，一个AUV在一次任务中显然不能到达所有的子任务点，尤其是在很大的环境内运行时（子任务点数量会很多）。因此，需要在完成任务数量和花费时间之间做一个折中。
本次matlab实现中，在二维场景首先进行尝试。路径点（子任务点）人为实现指定，网络图中的边根据相互距离确定。路径评价使用路径长度。先尝试选择出起点和终点之间的最短路径，对算法进行测试。后面再考虑加入子任务点，并加入新的路径评价标准。
3 matlab代码
task_planning.m
clear
map = imread('map2.jpg'); % 读入图片
map = rgb2gray(map); % 转换为灰度图
map = im2bw(map,0.2); % 转换为二值图
figure(1)
imshow(map); % 显示并设置坐标系
axis xy
axis on
hold on
% 任务点（路径点）集合
taskPoint = [23 40 20 42 30 131 137 125 220 268 224 274 244 299 331 355 391 389 464 502
74 185 281 387 489 270 379 492 172 264 337 427 505 46 174 405 505 287 396 494];
% 画出任务点，并标号
plot(taskPoint(1,:),taskPoint(2,:),'o','markersize',13,'markeredgecolor','r','LineWidth',2.5);
taskP_num = size(taskPoint,2); % 路径点数量
Edge = zeros(taskP_num); % 图的边
Distance = zeros(taskP_num); % 边距离
for i = 1:taskP_num
for j = i:taskP_num
dis = sqrt((taskPoint(1,i)-taskPoint(1,j))^2 + (taskPoint(2,i)-taskPoint(2,j))^2);
if dis < 180 && dis > 80
plot([taskPoint(1,i),taskPoint(1,j)],[taskPoint(2,i),taskPoint(2,j)],'--g','LineWidth',1.5);
Edge(i,j) = 1;
Edge(j,i) = 1;
else
dis = inf;
end
Distance(i,j) = dis;
Distance(j,i) = Distance(i,j);
end
end
text(taskPoint(1,1:9)-3,taskPoint(2,1:9)+1.5,num2cell(1:9));
text(taskPoint(1,10:20)-7.5,taskPoint(2,10:20)+1.5,num2cell(10:20));
% 算法参数
max_interation = 110; % 最大迭代次数
ants_num = 80; % 蚁群数量
Alpha = 1.5; % 参数
Beta = 1.2; % 参数
evaporation_rate = 0.15; % 挥发率
Q = 10; % 参数
heuristic_factor = 10./Distance; % 启发因子
pheromone = ones(taskP_num); % 信息素矩阵
path_matrix = zeros(ants_num, taskP_num); % 路径矩阵
n = 1;
best_path = zeros(max_interation,taskP_num);% 最好路径
best_pathcost = []; % 最好的路径代价值
% 开始迭代
while n <= max_interation
% rand_pose = [];
% for i = 1:(ceil(ants_num/taskP_num))
% rand_pose = [rand_pose, randperm(taskP_num)];
% end
path_matrix(:,1) = ones(ants_num,1); % 假设所有蚂蚁初始都在起始位置
tourend = []; % 已经到达终点的蚂蚁编号
flag = 0; % 标志变量
for j = 2:taskP_num % 循环开始每只蚂蚁的旅程
for i = 1:ants_num
if (flag ~= 0)
if i == tourend(find(tourend == i,1))
continue;
end
end
visited = path_matrix(i, 1:j-1); % 已经访问过的任务点
unvisited = zeros(1,taskP_num-j+1); % 还没有访问的任务点
probablity = []; % 待选任务点的概率值
can_num = 1; % 待选任务点数量
candidate_waypoint = []; % 下一步待选择的任务点数组
for k = 1:taskP_num, % 剔除已经访问过的点，和不能到达的点
if isempty(find(visited==k, 1)) && (heuristic_factor(k,visited(end)) ~= 0)
candidate_waypoint(can_num) = k;
can_num = can_num+1;
end
end
if isempty(candidate_waypoint) % 检查待选路径点数组是否为空，为空说明当前蚂蚁已经结束本次旅程（即已经到达目标点）
flag = flag + 1; % 若已经结束旅程，记录在数组tourend
tourend(flag) = i;
continue;
end
for k = 1:size(candidate_waypoint,2), % 计算待选的每种选择的概率
probablity(k) = (pheromone(visited(end),candidate_waypoint(k))^Alpha) * (heuristic_factor(visited(end),candidate_waypoint(k))^Beta);
end
probablity = probablity / sum(probablity);
cum_pro = cumsum(probablity); % 计算累积概率
rand_num = rand; % 轮盘赌策略选择下一任务点
% select = find(cum_pro >= rand_num, 1);
for k = 1:size(cum_pro,2)
if cum_pro(k) >= rand_num,
select = k;
break;
end
end
next_waypoint = candidate_waypoint(select); % 下一个访问的任务点
if next_waypoint == 20
flag = flag + 1;
tourend(flag) = i;
end
path_matrix(i,j) = next_waypoint; % 路径记录数组
end
end
path_cost = zeros(ants_num,1); % 路径代价值
unusable_path = []; % 不满足条件的路径点序列
unuse_num = 0; % 不满足条件的路径点序列数目
pheromone_diff = zeros(taskP_num,taskP_num); % 信息素增量
for i = 1:ants_num
path_i = path_matrix(i,:);
if isempty(find(path_i==20, 1)) % 路径起点都一样，检查路径中是否有终点序号（这里是20）
unuse_num = unuse_num + 1;
unusable_path(unuse_num) = i;
path_cost(i) = inf;
else
path_i = path_matrix(i,1:find(path_i==20, 1));
for j = 1:(length(path_i)-1)
path_cost(i) = path_cost(i) + Distance(path_i(j),path_i(j+1)); % 路径的代价值暂时设置为路径序列长度
end
for j = 1:(length(path_i)-1) % 计算信息素增量
pheromone_diff(path_i(j),path_i(j+1)) = pheromone_diff(path_i(j),path_i(j+1)) + Q/path_cost(i);
pheromone_diff(path_i(j+1),path_i(j)) = pheromone_diff(path_i(j),path_i(j+1));
end
end
end
best_pathcost(n) = min(path_cost); % 最小的路径代价值
best_path(n,:) = path_matrix(find(path_cost == best_pathcost(n),1),:); % 代价值最小的路径
pheromone = (1-evaporation_rate).*pheromone + pheromone_diff; % 更新信息素矩阵，考虑信息素的挥发
n = n+1;
end
% 画出最好的任务点序列
global_best_pathcost = min(best_pathcost)
best_pose = find(best_pathcost == global_best_pathcost,1);
global_best_path = best_path(best_pose,1:find(best_path(best_pose,:)==20,1))
for i = 1:(length(global_best_path)-1)
plot([taskPoint(1,global_best_path(i)),taskPoint(1,global_best_path(i+1))],[taskPoint(2,global_best_path(i)),taskPoint(2,global_best_path(i+1))],'--r','LineWidth',2);
end4 运行结果
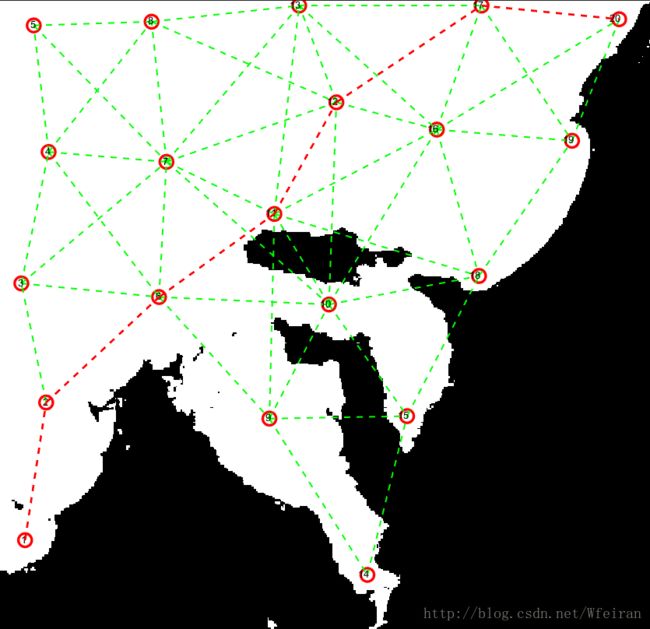
5 结果分析
代码可以生成一条从起点到终点的较优的任务序列，但每次运行结果有可能会不一样，暂时不知道是什么原因，后面再修改。
参考文献：
[1]Marco Dorigo, Gianni Di Caro, and Luca M. Gambardella. 1999. Ant algorithms for discrete optimization. Artif. Life 5, 2 (April 1999), 137-172. DOI=http://dx.doi.org/10.1162/106454699568728