NLP-2：Attention && Transformer

以下内容来自贪心学院NLP直播课。
简介： ELMo等基于深度学习的方法可以有效地学习出上下文有关词向量，但毕竟是基于LSTM的序列模型，必然要面临梯度以及无法并行化的问题，即便结合使用注意力机制，这里我们重点来讲解Transformer模型，它的核心是Self-Attention机制，并且Transformer也是BERT的核心组成部分。

1. Seq2seq

在Transformer之前 做翻译的时候，一般用基于RNN的Encoder-Decoder模型。从X 翻译到Y。

但是上面的模型的核心是基于RNN的,这也是模型的问题所在。

因为RNN有梯度消失的问题（LSTM/GRU只是缓解这个问题，并未彻底解决）
另外RNN 有时间上的方向性，不能用于并行操作。Transformer 摆脱了RNN这种问题。

2. Transformer

Transformer 的提出 使深度NLP可以不用RNN。

Transformer模型：左侧Encoder, 右侧Decoder.

• Encoder：
  Input embedding + Positional Encoding --> Nx(Multi-Head Attention + Feed Forward)
• Decoder：
  Output embedding + Positional Encoding(with mask) --> Nx(Self - Masked Multi-Head Attention layer + Cross attention + FeedForward)

在Encoder layer 如何运作？

Encoder 里面有 self-attention + FeedForward.
Self-attention 是 把 X（input embedding）转成 Z. 这里的转换是结合所有的输入，通过self-attention 转成Z输出，所以这里Z 对应的每个矩阵都是结合了上下文的矩阵。
FNN 是全连接层：把Z输出成R，这里面是单纯的全连接神经网络。只是将Z转换成R。

3. Self-Attention 机制详解

我们来看self-attention 是如何工作的？是如何把X 映射成Z？
请注意： self-attention 的目的是 句子内部，一些词之间的 关联性或者说 相关性 的强弱程度。(翻译模型Encode-Decoder 里面 有其他的attention 是输入和输出之间的attention，不是句子内部的self-attention)

X1 和X2 分别同时乘上 $W^Q,W^K,W^V$ 得到 q1,q2, k1,k2, v1,v2. 这里所有输入 Xi 都乘上相同的$W^Q,W^K,W^V$ ，所以在一定程度有一定的关系。
然后$x_1$ 对应的score 是 $q_1\ast k_1,q_2\ast k_2,q_1\ast k_3$… —>divide by 8 --> softmax 得到一系列概率值， 然后将 v1，v2, v3 分别与概率值对应相乘，得到softmax * value 一系列 向量矩阵，最后通过 Sum 得到$Z_1$.

W(q,k,v) 是随机初始化的，由于X1,X2,X3。。最初的embedding是没有关系的，通过与W(qkv)相乘，得到使得 X1,X2,X3 有关联的 query，key，value. 在self-attention 时，就是同过Xi 的 query 与 每个输入单词的 key 相乘（除以8)，然后softmax得到 Xi 与 所有 输入单词 之间的相关概率，然后将 每个单词的value 与 这个概率相乘 就可以得到 与Xi 相关的向量，最后将所有的向量相加，就可以得到 Xi 对应的 Zi。这里的Zi 就是self-attention 输出的Zi.

Self Attention 的 向量化计算（可以加速）。

Multi-Head attention:
X与不一样的W(qkv)相乘，会产生出不一样的 query key value。
如果我们随机初始化 不同的 W0,W1,W2，那么X与Wi 相乘会得到不同的 KQV，那么就会得到不同角度的 KQV，每个 Head 产生一个 Zi，既多个角度的Z。

论文中使用了8个Head。 每个head 都会有一个z输出.所以有 $Z_0,Z_1,.Z_7$ 每一个z 里面都是X 通过 Head-i 输出的。
我们最终是希望输入一个X 输出一个Z，尽管算法里面用的8个head，我们如何输出一个Z？
通过全连接网络。
将Zi 拼接，然后与一个W 相乘 得到 一个Z。


至此为止 从X 通过Self-attention 得到Z。
然后Z通过一个FNN得到R。 然后R 再继续通过这样的Encoder(Self-attention-FNN) 又可以继续得到 R作为输入时对应的Z 和 new R。

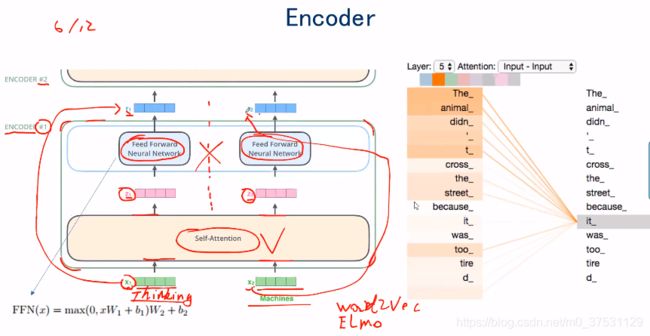
可以看出 橙色 这个 head 中 学习到的 it 与 the animal 相关性更高。
绿色 head中 it 与 tire d_ 更相关。

所以不同的head 学到的内容是不一样的。

4. Positional Encoding

在输入端，不仅仅是 word embedding， 还需要 positional encoding. 也就是单词之间的距离信息。

在这个论文中，距离是通过正弦和余弦来产生的。
输入是 单词在原来句子中的位置pos(0,1,2,3,…)， 和 i （输出的维度上的位置 2i = 0,2,4… 2i+1=1,3,5… 奇数位置用cos 函数，偶数位置用sin函数）


encoding的维度是 4 ，也就是 d_model = 4
分子是 pos， 分母为 $2_i/d_{model}$
PE(pos=0, 2i=0): pos = 0是原始输入里面单词位置为０，2i=0 是输出的维度中 在第0个位置，所以第一个$POS(pos,0)=sin(pos/10000^0)$
前2个位置：i=0 （2i=0, 2i+1 = 1）, 后2个位置: i=1: （2i=2， 2i +1=3）所以对应的输出position encoding 为【sin(pos), cos(pos), sin(pos/100), cos(pos/100)】

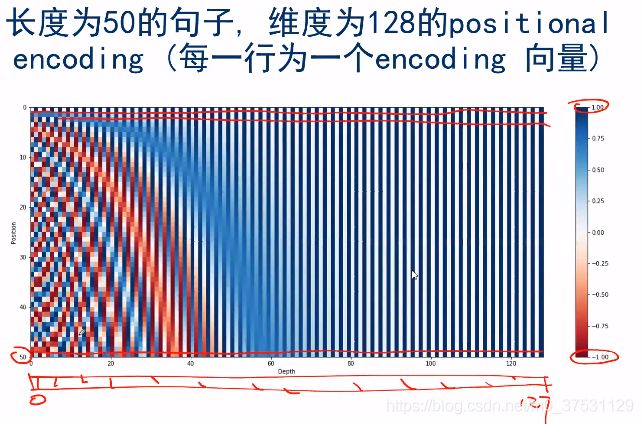
不同位置上的值产生的encoding 是独特的。

虽然作者用这种方式，但是这不是唯一的positional encoding 方式。只要我们用一种方式 可以使 每个词位置是独立的 并且可以计算距离的。

横坐标 和纵坐标 都是 position （0-49）, 通过 每个单词position encoding 自己与自己做点积，得到的 值是最大的（中间颜色最深的）。离该单词越远的 点积 值越小（颜色越淡）。
也就是position encoding 通过点积的结果 来 表示 距离远近。

5. Layer Normalization

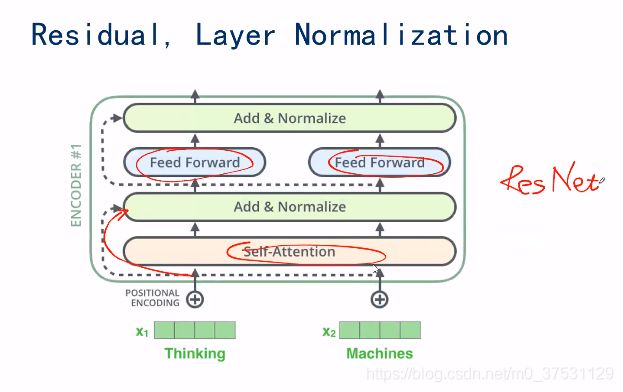
除了 Self-attention 和FNN， 还有 ResNet， 这个跳跃连接。
还有 一个 Layer normazation 这个是一个 正则化的方式。

Layer normalization 是通过对一个向量计算均值，然后将每一个值减去均值,除以方差，归一化为均值为0，方差为1，然后再进行缩放（均值和方差的缩放）


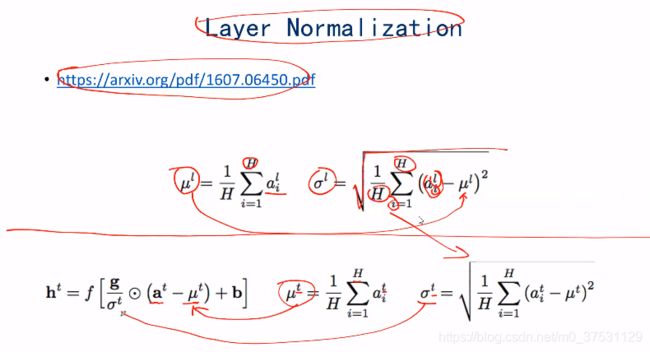
layer normalization 可以避免batch size 不同的影响。

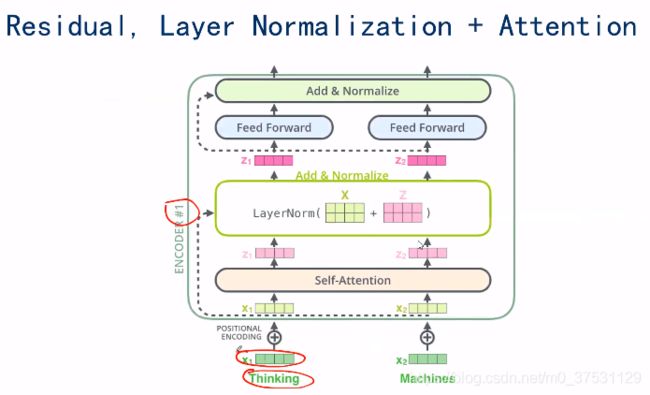
Embedding; 可以简单的word2vec 或者 Elmo的 embedding
positional embedding
Self-attention
Resnet
Layer norm
FNN
layer norm

6. Transformer Encoder 与 Decoder

Decoder Vs Encoder：
区别在于 Decoder多了一个Encoder-Decoder Attention，并且Decoder中有一个mask 因为我们在训练时需要覆盖还没有输出的单词（通过0,0,0,1，1,1,1,1：1为mask，0为可见）。 后面增加了一个linear + softmax 预测输出。
在Decoder中， Masked Attention ：encoder的输出m 与W(k,v)相乘， 告诉我们此处的 Key 和 value 是什么，Y自身与W(q)只产生query。这一层attention产生的$Z=v_1\ast {\theta }_1+v_2\ast {\theta }_2+..$ 其中${\theta }_i$ 是softmax(q*k/8) 这一层建立起 encoder 与 decoder 的联系。




Transformer的损失函数 是 交叉熵损失（很基础）

Label smooting： 就是准备标签时 不用绝对的0 1 序列，可以通过smoothing 也就是正确的值 对应的不是1 而是比如0.95 其他的值就是0.05/(n-1)

7. 总结

在Decoder中， Masked Attention ：encoder的输出m 与W(k,v)相乘， 告诉我们此处的 Key 和 value 是什么，Y自身与W(q)只产生query。

Others

可以结合本人简书里面的 Transformer中文介绍
Transformer