寻找最优初始学习率-Keras实现
参考知乎某大牛的回答,原链接为:如何找到最优学习率
经过了大量炼丹的同学都知道,超参数是一个非常玄乎的东西,比如batch size,学习率等,这些东西的设定并没有什么规律和原因,论文中设定的超参数一般都是靠经验决定的。但是超参数往往又特别重要,比如学习率,如果设置了一个太大的学习率,那么loss就爆了,设置的学习率太小,需要等待的时间就特别长,那么我们是否有一个科学的办法来决定我们的初始学习率呢?
一个简单的办法
Leslie N. Smith 在2015年的一篇论文“Cyclical Learning Rates for Training Neural Networks”中的3.3节描述了一个非常棒的方法来找初始学习率,同时推荐大家去看看这篇论文,有一些非常启发性的学习率设置想法。
这个方法在论文中是用来估计网络允许的最小学习率和最大学习率,我们也可以用来找我们的最优初始学习率,方法非常简单。首先我们设置一个非常小的初始学习率,比如1e-5,然后在每个batch之后都更新网络,同时增加学习率,统计每个batch计算出的loss。最后我们可以描绘出学习的变化曲线和loss的变化曲线,从中就能够发现最好的学习率。
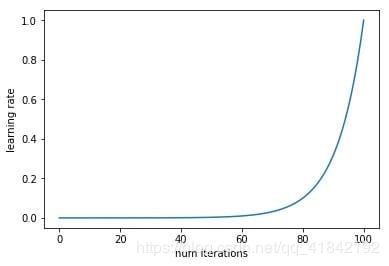
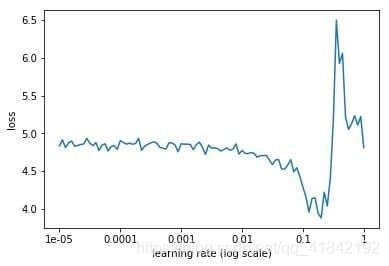
下面就是随着迭代次数的增加,学习率不断增加的曲线,以及不同的学习率对应的loss的曲线。
从上面的图片可以看到,随着学习率由小不断变大的过程,网络的loss也会从一个相对大的位置变到一个较小的位置,同时又会增大,这也就对应于我们说的学习率太小,loss下降太慢,学习率太大,loss有可能反而增大的情况。从上面的图中我们就能够找到一个相对合理的初始学习率,0.1。
之所以上面的方法可以work,因为小的学习率对参数更新的影响相对于大的学习率来讲是非常小的,比如第一次迭代的时候学习率是1e-5,参数进行了更新,然后进入第二次迭代,学习率变成了5e-5,参数又进行了更新,那么这一次参数的更新可以看作是在最原始的参数上进行的,而之后的学习率更大,参数的更新幅度相对于前面来讲会更大,所以都可以看作是在原始的参数上进行更新的。正是因为这个原因,学习率设置要从小变到大,而如果学习率设置反过来,从大变到小,那么loss曲线就完全没有意义了。
PyTorch实现
上面已经说明了算法的思想,说白了其实是非常简单的,就是不断地迭代,每次迭代学习率都不同,同时记录下来所有的loss,绘制成曲线就可以了。下面就是使用PyTorch实现的代码,因为在网络的迭代过程中学习率会不断地变化,而PyTorch的optim里面并没有把learning rate的接口暴露出来,导致显示修改学习率非常麻烦,所以我重新写了一个更加高层的包mxtorch,借鉴了gluon的一些优点,在定义层的时候暴露初始化方法,支持tensorboard,同时增加了大量的model zoo,包括inceptionresnetv2,resnext等等,提供预训练权重,model zoo参考于Cadene的repo。目前这个repo刚刚开始,欢迎有兴趣的小伙伴加入我。
下面就是部分代码,近期会把找学习率的代码合并到mxtorch中。这里使用的数据集是kaggle上的dog breed,使用预训练的resnet50,ScheduledOptim的源码点这里。
criterion = torch.nn.CrossEntropyLoss()
net = model_zoo.resnet50(pretrained=True)
net.fc = nn.Linear(2048, 120)
with torch.cuda.device(0):
net = net.cuda()
basic_optim = torch.optim.SGD(net.parameters(), lr=1e-5)
optimizer = ScheduledOptim(basic_optim)
lr_mult = (1 / 1e-5) ** (1 / 100)
lr = []
losses = []
best_loss = 1e9
for data, label in train_data:
with torch.cuda.device(0):
data = Variable(data.cuda())
label = Variable(label.cuda())
# forward
out = net(data)
loss = criterion(out, label)
# backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
lr.append(optimizer.learning_rate)
losses.append(loss.data[0])
optimizer.set_learning_rate(optimizer.learning_rate * lr_mult)
if loss.data[0] < best_loss:
best_loss = loss.data[0]
if loss.data[0] > 4 * best_loss or optimizer.learning_rate > 1.:
break
plt.figure()
plt.xticks(np.log([1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1]), (1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1))
plt.xlabel('learning rate')
plt.ylabel('loss')
plt.plot(np.log(lr), losses)
plt.show()
plt.figure()
plt.xlabel('num iterations')
plt.ylabel('learning rate')
plt.plot(lr)
Keras的实现
原博客并没有给出Keras的实现,我就自己写了一个回调函数类,基本上能实现需要的功能,源代码如下:
class LearnRateTest(Callback):
def __init__(self, base_lr=0.00001, max_lr=1):
super(LearnRateTest, self).__init__()
self.base_lr = base_lr
self.lr = self.base_lr
self.max_lr = max_lr
self.iterations = 0
# 学习率的增长率
self.lr_mult = (1 / 1e-5) ** (1 / 100)
self.history = {}
def on_train_begin(self, logs={}):
K.set_value(self.model.optimizer.lr, self.base_lr)
def on_batch_end(self, batch, logs=None):
logs = logs or {}
self.iterations += 1
self.lr = self.lr * self.lr_mult
if self.lr > self.max_lr:
self.lr = self.max_lr
# 把logs的信息复制到我们的history字典里
self.history.setdefault('lr',[]).append(K.get_value(self.model.optimizer.lr))
self.history.setdefault('iterations', []).append(self.iterations)
for k, v in logs.items():
self.history.setdefault(k, []).append(v)
# 设置这一批次的学习率
K.set_value(self.model.optimizer.lr, self.lr)
print()
print("当前的批次为:{},当前的学习率为:{}".format(self.iterations, self.lr))
使用示例:
lr_test = LearnRateTest(base_lr=0.00001, max_lr=1)
model.fit(X_train, Y_train, callbacks=[lr_test])
df = pd.DataFrame(lr_test.history)
df.to_excel("result.xlsx", index=False)