机器学习：Logisitic回归

---

机器学习 深度学习 NLP 搜索推荐 等 索引目录

---

Logistic回归（logistic regression）是统计学习中经典的分类方法，其模型属于对数线性模型。

---

1.Logistic分布（logistic distribution）

什么是logistic分布？
我们假设有一组变量$X$是连续随机变量，当$X$具有下列分布函数和密度函数时，我们就说$X$服从Logistic分布，
分布函数：
$$F(x)=P(x\le x)=\frac{1}{1+e^{-(x-\mu )/\gamma }}$$
密度函数：
$$f(x)=F^{\prime }(x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma (1+e^{-(x-\mu )/\gamma }{)}^2}$$

式中，$\mu$位置参数，$\gamma >0$为形状参数。

logistic分的密度函数$F(x)$和分布函数$F(x)$的图形如下所示：

分布函数属于logistic函数，是一条S曲线（Sigmoid），可以看出，曲线在中心附近增长速度较快，在两端增长速度较慢，形状参数$\gamma$的值越小，曲线在中心附近增长得越快。

2.二项logistic回归模型

什么是二项logistic回归模型？

二项logistic回归模型是一种分类模型，其模型是如下的条件概率分布：

$$P(Y=1|x)=\frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)}$$
$$P(Y=0|x)=\frac{1}{1+exp(w\cdot x+b)}$$

其中x是输入，$Y\in \{0,1\}$ 是输出，$w$和$b$是参数，$w$为权重向量，$b$为偏置。

上述两式即求出了实例$x$的条件概率，logistic回归通过比较这两个条件概率的大小，将实例$x$分到概率值较大的那一类。

3.模型参数估计

对于给定的训练数据集$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中$y_i\in \{0,1\}$，这里应用极大似然法来估计模型参数。

假定:
$$\begin{gathered} P(y=1|x;w)=h_w(x) \\ P(y=0|x;w)=1-h_w(x) \end{gathered}$$
则
$$P(y|x;w)=h_w(x{)}^y(1-h_w(x){)}^{(1-y)}$$

似然函数为
$$\begin{array}{rl}L(w)& =p(Y|X;w)\\ & =\prod _{i=1}^{N}p(y^{(i)}|x^{(i)};w)\\ & =\prod _{i=1}^N(h_w(x^{(i)}){)}^y(1-h_w(x^{(i)}){)}^{(1-y^{(i)})}\end{array}$$

接下来就是取对数似然函数，对 对数似然函数取极大值，即得到w的估计值。

---

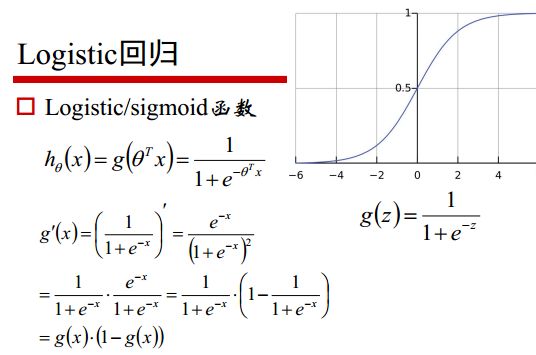
对对数函数求导的求导公式略繁琐，就以下面几张图片做展示（来自邹博老师的课件），这里的$\theta$即为我们上面所描述的$w$。

---