特征提取模型的轻量化之路（一）

一、 参数量和理论计算量

1、计算公式：

假设卷积核大小为 $K_h\times K_w$，输入通道数为 $C_{in}$，输出通道数为$C_{out}$，输出特征图的宽和高分别为$W$和$H$，这里忽略偏置项

• CONV 标准卷积层：

1. params：$K_h\times K_w\times C_{in}\times C_{out}$
2. FLOPs：$K_h\times K_w\times C_{in}\times C_{out}\times H\times W=params\times H\times W$

• FC 全连接层（相当于 k=1）：

1. params： $C_{in}\times C_{out}$
2. FLOPs：$C_{in}\times C_{out}$

二、轻量级网络

1、 SqueezeNet

文章的的核心是提出了一个fire module， 如下图所示：

在fire module中有三个可调参数：s, e1, e3分别代表各个卷积核的个数。在论文中给出的参数设置方法是$e_1=e_3=4s_1$。

我对Fire module的理解是：

• 这里是一个简化的Inception block。

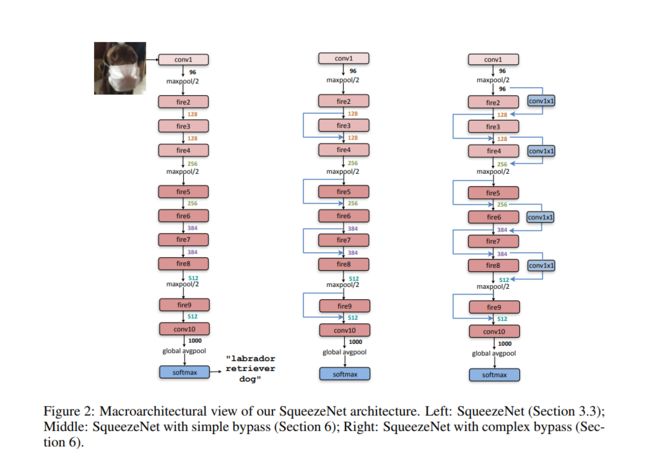
整个SqueezeNet的架构设计思路类似于VGGNet—对fire module进行堆叠。其结构图如下。

2、 深度可分离卷积

Inception 模块的背后存在这样的一种假设：卷积层通道间的相关性和空间相关性是可以退耦合的，将它们分开映射，能达到更好的效果（the fundamental hypothesis behind Inception is that cross-channel correlations and spatial correlations are sufficiently decoupled that it is preferable not to map them jointly.）。

常规的卷积操作是实现通道相关性和空间相关性的联合映射。
因此就有了这样一个问题：为什么要同时考虑图像区域和通道?为什么不把通道和空间区域分开？
因此深度可分离卷积提出了一种新的思路：对图像和通道分别进行不同的卷积操作。

2.1、普通卷积

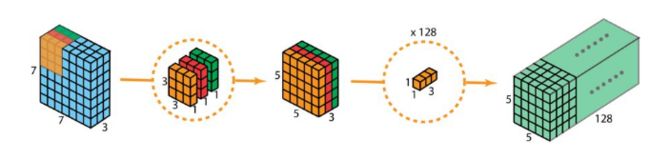
假设输入为$N\times 7\times 7\times 3$，同时有128个3*3卷积，假设padding=0，stride=1，那么普通卷积的输出是N*5*5*128。空间维度降低，深度增大。

2.2、 空间可分离卷积

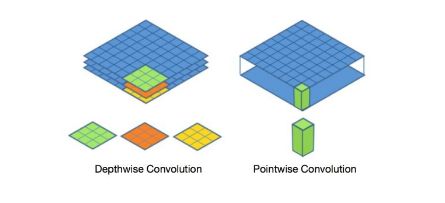
可以概括为：depth-wise convolution 与 point-wise(1*1) convolution的结合，完成了一个普通卷积的功能，相较于普通卷积大幅度的减少了运算量。

第一步（depth-wise convolution）：不直接使用3*3*3的卷积核来进行卷积，而是将他们分成3个3*3*1的卷积，分别与输入的每层通道进行卷积（仅与一个通道卷积，而非所有通道！）。这样就得到了3个5*5*1的feature map，接着将他们合并（concat）在一起。

• Note：采用 depth-wise convolution 会有一个问题，就是导致 信息流通不畅 ，即输出的 feature map 仅包含输入的 feature map 的一部分，MobileNet 采用了 point-wise(1*1) convolution 【下述第二步】帮助信息在通道之间流通

在这一步中，我们只考虑了图像区域的信息映射

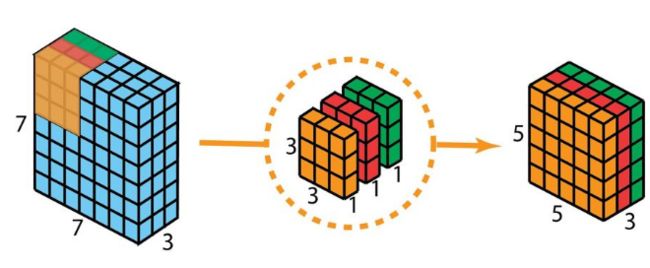
第二步：在第一步中，由于需要使用单层卷积核来对应输入的每一层做计算，导致这样计算后的输出通道数是等于输入通道数的。要扩充通道数到我们所需要的大小就需要使用n个113大小的卷积核来进行控充（修改深度）。
这一步中，我们考虑的是深度区域的信息映射

通过这两个步骤，深度可分卷积将输入的（7×7×3）变换到输出的（5×5×128）大小，达到了与普通卷积相同的效果。

下图展示了深度可分卷积的整个过程。

2.3、 对比总结

经过上述描述，深度可分离卷积相较于普通卷积的优势在哪里呢？ 似乎不是参数量。
答案是：操作数量（运算）的减少。

1. 普通卷积：
   128个3x3x3的卷积核移动了5（横向）x5（纵向)次，也就是进行了$128\ast 3\ast 3\ast 3\ast 5\ast 5=86400$次乘法。
2. 深度可分离卷积：
   第一步：3个3x3x1的卷积核移动了5x5次，$3\ast 3\ast 3\ast 1\ast 5\ast 5=675$次乘法。
   第二步：128个1x1x3的卷积核移动了5x5次，$128\ast 1\ast 1\ast 3\ast 5\ast 5=9600$次乘法。
   因此总共做了$9600+675=10275$次乘法。这只有普通卷积的12%。

这可以大幅度的提高算法的运行效率。

更泛化的来讲：

假设输入为$H\times W\times D$，卷积核大小为 $K_h\times K_w$，$stride=1,padding=0$ 输入通道数为 $C_{in}$，输出通道数为$C_{out}$，输出特征图的宽和高分别为$(H-h+1)$和$(W-h+1)$，

1. 对于普通卷积所需的乘法次数
   $Nums\_Norm=C_{out}\times K_h\times K_w\times C_{in}\times (H-h+1)\times (W-h+1)$

2. 对于深度可分卷积所需的乘法次数:
   $Nums\_Depth=C_{in}\times K_h\times K_w\times 1\times (H-h+1)\times (H-h+1)+C_{out}\times 1\times 1\times C_{in}\times (H-h+1)\times (W-h+1)$

两者之比为： $\frac{Nums\_Depth}{Nums\_Norm}$ = $\frac{1}{C_{out}}$ + $\frac{1}{K_h\times K_w}$

其中$C_{out}$是输出通道数，$K_h\times K_w$是卷积核大小。

现代大多数架构的输出层通常都有很多通道，可达数百甚至上千。对于这样的层（Nc >> h），则上式可约简为$1/h²$。基于此，如果使用 3×3 过滤器，则 2D 卷积所需的乘法次数是深度可分卷积的 9 倍。如果使用 5×5 过滤器，则 2D 卷积所需的乘法次数是深度可分卷积的 25 倍。
使用深度可分卷积有什么坏处吗？当然是有的。深度可分卷积会降低卷积中参数的数量。因此，对于较小的模型而言，如果用深度可分卷积替代 2D 卷积，模型的能力可能会显著下降。因此，得到的模型可能是次优的。但是，如果使用得当，深度可分卷积能在不降低你的模型性能的前提下帮助你实现效率提升。

3、MobileNet

3.1、MobileNet v1

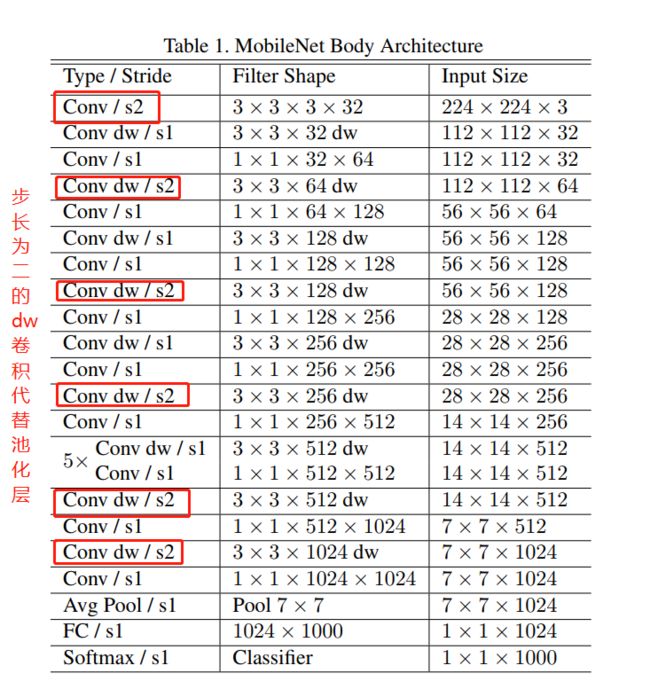
MobileNet v1网络架构如下图：

其中dw就是（depth-with），Conv/s1就是pw卷积。具体如下图右边所示。

下表展示了使用普通 $3\times 3\times C_{in}$ 卷积与使用深度可分离卷积的MobileNet在ImageNet上的对比（从准确率，乘法和加法运算次数，参数量方面）。

• 可以看到参数量和运算次数得到了大幅度的减少，但这也导致损失了一些精度
  

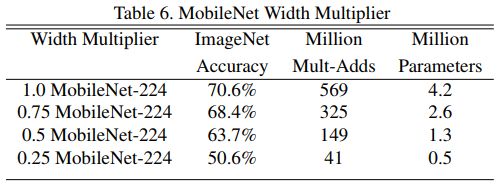
在这个使用dw卷积架构的基础上，MobileNet v1还对所有的卷积核数量统一乘以缩小因子 $\alpha$$\in$$[0,1]$（典型值为$1，0.75，0.5，0.25$）来压缩网络（四舍五入）。
因此Depth-wise+Point-wish的总计算量进一步压缩为:
$Nums\_Depth=\alpha C_{in}\times K_h\times K_w\times 1\times (H-h+1)\times (H-h+1)+\alpha C_{out}\times 1\times 1\times \alpha C_{in}\times (H-h+1)\times (W-h+1)$

当然了这是以精度损失为代价的，下表显示了$\alpha$不同时，MobileNet v1在ImageNet上的性能：

下表显示了：MobileNet与GoogleNet,VGG在ImageNet下的对比。

• MobileNet v1总结:

1. 该网络的核心思想是采用 depth-wise 卷积操作，在相同的权值参数数量的情况下，相较于 标准卷积操作，可以成倍的减少运算量，达到网络模型提速的目的。
2. 单独采用 depth-wise 卷积时，会导致通道间的信息流通不畅，即输出的 feature map中仅包含了输入 feature map 的一部分信息。MobileNet采用的的解决方案是： 引入用 point-wise卷积来融合通道间信息，解决这个问题。

3.2、MobileNet v2

与MobileNet v1的不同点:

1. 引入了类似于残差网络中的shortchut结构—Inverted Residuals。在进行dw之间先进行1x1卷积增加输入feature map的通道数，实现feature map的扩张 。（Inverted Residuals ）原因是：低维的feature map输入限制了dw卷积对特征的提取。
2. 去掉了位于dw卷积后部的point-wise卷积之后的Relu激活函数，文中称之为Linear Bottlenecks。原因是：作者认为激活函数在高维空间能有效的增加非线性，而在低维空间时线性效果会好于非线性(信息损失较少)。
3. 模型中其余的Relu都改用了Relu6：$f(x)=min(max(x,0),6)$。其优点是We use Relu6 as the non-linearity because of its robustness when used with low-precision computation.
4. 去除了fc层，转为全卷积神经网络。

1. inverted residulas倒残差模块:

• 残差模块：输入首先经过$1\times 1$的卷积进行压缩，然后使用$3\times 3$的卷积进行特征提取，最后在用$1\times 1$的卷积把通道数变换回去。整个过程是“压缩-卷积-扩张”。这样做的目的是减少$3\times 3$模块的计算量，提高残差模块的计算效率。
• 倒残差模块：输入首先经过$1\times 1$的卷积进行通道扩张，然后使用$3\times 3$的depth-wise卷积，最后使用$1\times 1$的point-wise卷积将通道数压缩回去。整个过程是“扩张-卷积-压缩”。为什么这么做呢？因为depth-wise卷积不能改变通道数，导致特征提取受限于输入的通道数。如果输入feature map通道很少的话，DW卷积只能在低维度上工作，这样效果并不会很好，因此我们要“扩张”通道（使用pw卷积来实现）。对于扩展因子的选取，小网络使用小的扩展因子，大网络使用大的扩展因子，推荐是5~10，论文中 $t=6$。

与v1, resnet的比较如下图，可以看到:

• ResNet 先降维 (0.25倍)、卷积、再升维。
• MobileNetV2 则是 先升维 (6倍)、卷积、再降维。

2. Linear Bottlenecks

简单的说就是把dw卷积之后的pw卷积跟的Relu激活函数（非线性）删除掉了（说的有点拗口），因此变为了线性block。这里没有做任何多余的操作。不要想太多哇。

综上我们再来直观的对比一下MobileNet v1和v2的block，见下图：

可以看到，用于下采样的$stride=2$的block，由于输入feature map与输出feature map的size不同，所以没有采用short cut操作。

v2 架构图:

可以看到最后一层由fc变为了1x1的卷积层。

性能对比:

再ImageNet下，v2比v1的更加准确的同时，参数量和运算量反而更小，具体对比见下图：

总结：

1. 引入inverted residulas倒残差模块，用于高dw卷积操作时的维度。之所以使用倒残差，是因为如果直接用残差的话，先降维之后，在dw操作时的维度会更少明显不可以。所以好像有点为了引入残差而使用的？不过这也证明了short cut模块确实好！！！。
2. 去掉每个block的最后一个Relu6函数，减少信息的损失。
3. 相较于v1，速度更快，参数更少，精准度更高。

3.3、MobileNet v3

关键技术:

1. 网络的架构基于神经结构搜索（NAS）
2. 引入基于squeeze and excitation结构的轻量级注意力模型(SE)
3. 使用了一种新的激活函数h-swish(x)
4. 网络结构搜索中，结合两种技术：资源受限的NAS（platform-aware NAS）与NetAdapt
5. 修改了MobileNetV2网络端部最后阶段
6. 引入MobileNetV1的深度可分离卷积
7. 引入MobileNetV2的具有线性瓶颈的倒残差结构

因此v3中我们需要搞清楚的重点就是：

• 神经结构搜索（NAS）
• 轻量级注意力模型（SE）
• h-swish(x)激活函数
• 结构的变化

1)、 h-swish激活函数

swish最由google brain在2017年提出的论文，其作者认为，swish具备无上界有下界、平滑、非单调的特性。并且swish在深层模型上的效果优于ReLU。仅仅使用Swish单元替换ReLU就能把MobileNet,NASNetA在 ImageNet上的top-1分类准确率提高0.9%，Inception-ResNet-v的分类准确率提高0.6%。

$swish[x]=x\cdot \sigma (x)$

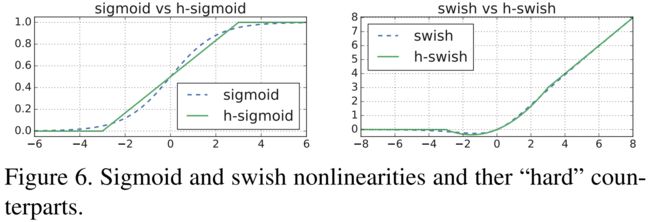
MobileNet v3中作者也尝试利用swish当代替ReLU，发现它可以显著提高神经网络的精度。在嵌入式设备中计算sigmoid函数需要较大的开销。因此对其做出了改进，提出了h-swish，主要目的是让swish变的hard（the hard version of swish becomes
）。

$h-swish[x]=x$$\frac{ReLU6(x+3)}{6}$

这样修改的优点是：

1. Relu6的优化实现在所有的软硬件框架上都可用。
2. 在量化模型下，他消除了由于近似S形的不同实现所引起的潜在的数值精度损失。
3. Relu6可以作为一个分段函数来实现，以减少内存的占用数量。

我们可以把hard形式的激活函数认为是原激活函数在低精度运算时的一种表现形式。作者在实验中发现使用hard-swish的情况下，16个卷积核达到的精度与使用ReLU或swish作为激活函数的32个过滤器相同的精度，这将节省额外的2毫秒和1000万MAdds的计算量。

文中还指出：应用非线性的成本随着网络的深入而降低，因为每层激活内存通常在分辨率下降时减半。顺便说一句，我们发现swish的大部分好处都是通过在更深层次上使用它们来实现的。因此在我们的架构中，我们只在模型的后半部分使用h-swish。

2)、 结构的变化

作者认为，基于V2模型中的倒残差结构中，最后一层使用1×1卷积(pw)来构建，这样可以便于拓展到更高维的特征空间。这样做的好处是，在预测时，有更多更丰富的特征来满足预测，但是同时也引入了额外的计算成本与延时。
因此，需要改进的地方就是要保留高维特征的前提下减小延时。首先将avg pooling提前，在使用pw卷积进行扩张后，就紧接池化层，激活函数，然后用1x1卷积在池化层之后进行输出。
具体的结构变化如下图所示：

3)、 Squeeze-Excite(SE)模块

4)、 NAS模块
具体内容还是等我先研读完NAS和SE模型后在来讲吧。[捂脸，逃]。会专门出一篇文章详细进行详细讲解的。到时候回来补充链接。

5)、 整体架构
MobileNetV3定义了两个模型: MobileNetV3-Large和MobileNetV3-Small。V3-Large是针对高资源情况下的使用，相应的，V3-small就是针对低资源情况下的使用。两者都是基于之前的简单讨论的NAS。
分别是下图的表1（large）和表二（small）。

就像之前所说的：只有在更深层次使用h-swish(HS)才能得到比较大的好处。所以在上面的网络模型中，不论大小，作者只在模型的后半部分使用HS。

三、小结

至此MobileNet v1,v2,v3就记录完了。
v1引入depth-wise卷积和point-wise卷积，然后进行堆叠。
v2中加入了inverted残差模块，取消了pw卷积后的激活函数，变为了全卷积神经网络。
v3中引入NAS，SE模块。使用新的激活函数h-wwish，修改了V2中的最后几层。
我们注意到无论哪个版本，其精髓就是深度可分离卷积。而深度可分离卷积就是加速运算的精髓。
为什么MobileNet这么快呢？ 参考这里。
总结一下就是卷积运算很费时间，提高卷积运算的效率就能提高运算速度。

• 文章中提到的部分结论：

1. v1~v3都舍弃了Max pooling层，因为模型小不易过拟合而更易于发生欠拟合的现像，因此加入Pooling会导致有用信息的丢失，增加欠拟合的可能。因此使用步长为2的卷积替代。
2. 低维的feature map输入会限制dw卷积对特征的提取，因此需要使用$1\times 1$卷积对其进行升维。
3. 普通的 $k\times k$ 2D 卷积所需的乘法次数是深度可分卷积的 $k^2$ 倍。e.g.: 5×5 卷积，则 2D 卷积所需的乘法次数是深度可分卷积的 25 倍。
4. 深度可分卷积会降低卷积中参数的数量。因此，对于较小的模型而言，深度可分卷积可能会导致模型的能力的显著下降。
5. Relu6函数在低精度运算时拥有更好的鲁棒性。
6. 高维空间向低维空间映射时使用非线性激活函数会导致信息的丢失（1x1卷积运算相当于把n维的信息线性相加压缩到1维中）。激活函数在高维空间能有效的增加非线性，而在低维空间时线性效果会好于非线性。所以一般1x1卷积后面都不跟Relu?
7. 应用非线性的成本随着网络的深入而降低，因为每层激活内存通常在分辨率下降时减半。
8. 最后一层使用1×1卷积(pw)来构建将feature map拓展到更高维的特征空间。这样做的好处是，在预测时，有更多更丰富的特征来满足预测，

N、参考文章

1. SQUEEZENET: ALEXNET-LEVEL ACCURACY WITH 50X FEWER PARAMETERS AND <0.5MB MODEL SIZE
   
2. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
3. Inverted Residuals and Linear Bottlenecks Mobile Networks for Classification, Detection and Segmentation
4. Searching for MobileNetV3
5. 纵览轻量化卷积神经网络：SqueezeNet、MobileNet、ShuffleNet、Xception
6. 『高性能模型』深度可分离卷积和MobileNet_v1
7. MobileNetV1 & MobileNetV2 简介
8. 轻量级神经网络“巡礼”（二）—— MobileNet，从V1到V3
9. MobileNet V2 论文初读
10. MobileNet系列
11. 一文读懂 12种卷积方法（含1x1卷积、转置卷积和深度可分离卷积等）