Cesium中笛卡尔坐标系到底是什么鬼

  使用Cesium开发三维GIS应用离不开笛卡尔坐标系，在CesiumJS中定义类型是Cartesian3，这是Cesium的基础数据类型，所有坐标最后均转换成这个类型参与三维渲染，包括屏幕坐标，地理坐标系坐标。那么问题来了，这个笛卡尔坐标系到底是什么鬼？常用的WGS84怎么转换成这个坐标系的？让我们来看看cesium源码一探究竟。

Cartesian3.js里面有个函数fromRadians ，将经纬度转换成Cartesian3，其中经纬度是wgs84转换成弧度的经纬度。

Cartesian3.fromRadians = function(longitude, latitude, height, ellipsoid, result) {
    //>>includeStart('debug', pragmas.debug);
    Check.typeOf.number('longitude', longitude);
    Check.typeOf.number('latitude', latitude);
    //>>includeEnd('debug');

    height = defaultValue(height, 0.0);
    var radiiSquared = defined(ellipsoid) ? ellipsoid.radiiSquared : wgs84RadiiSquared;

    var cosLatitude = Math.cos(latitude);
    scratchN.x = cosLatitude * Math.cos(longitude);
    scratchN.y = cosLatitude * Math.sin(longitude);
    scratchN.z = Math.sin(latitude);
    scratchN = Cartesian3.normalize(scratchN, scratchN);

    Cartesian3.multiplyComponents(radiiSquared, scratchN, scratchK);
    var gamma = Math.sqrt(Cartesian3.dot(scratchN, scratchK));
    scratchK = Cartesian3.divideByScalar(scratchK, gamma, scratchK);
    scratchN = Cartesian3.multiplyByScalar(scratchN, height, scratchN);

    if (!defined(result)) {
        result = new Cartesian3();
    }
    return Cartesian3.add(scratchK, scratchN, result);
};

1. 检验经纬度是否符合标准；

Check.typeOf.number('longitude', longitude);
Check.typeOf.number('latitude', latitude);

2. 如果高度为空赋值默认为0；

height = defaultValue(height, 0.0);

3. 如果坐标系为空默认赋值WGS84坐标系；

var radiiSquared = defined(ellipsoid) ? ellipsoid.radiiSquared : wgs84RadiiSquared;

4. 赋值地球球体半径（假设为1）在xy平面上的投影长度；
   cesium假设wgs84坐标系构成地球球体是xy平面的正圆，z轴稍微小一点扁椭球：
   
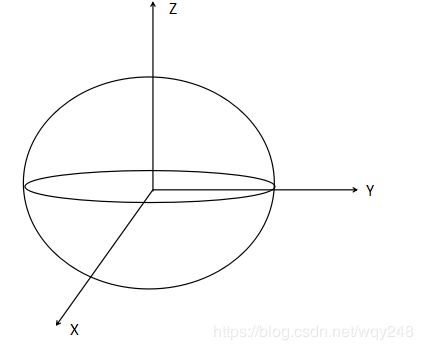
   如上图所示：x轴垂直纸面向上，wgs84坐标系定义的x，y平面圆是正圆，半径是6378137，xz或者yz的圆是椭圆，z轴的半径是：6356752.3142451793，定义如下：

var wgs84RadiiSquared = new Cartesian3(6378137.0 * 6378137.0, 6378137.0 * 6378137.0, 6356752.3142451793 * 6356752.3142451793);

var cosLatitude = Math.cos(latitude);

所以这句话的意思是假设球半径为1，这个半径投影到xy平面上的长度（当然由于这不是标准球，所以球半径不是固定的，但是在这里假设是一个标准球，直到下面第9步骤）。

5. 求出对应x轴坐标（假设球半径为1），用上一步求得的投影长度乘以经度的余弦，直接求得对应x轴坐标；
   

scratchN.x = cosLatitude * Math.cos(longitude);

6. 求出对应y轴坐标（假设球半径为1）；

scratchN.y = cosLatitude * Math.sin(longitude);

7. 求出对应z轴坐标（假设球半径为1），以上三步骤构成scratchN向量；

scratchN.z = Math.sin(latitude);

8. 求出scratchN的单位模向量赋值给scratchN本身，这样做的目的是把这个xyz轴数值同比例缩小到一个单位球，便于后面等比例变化；
   单位模的含义：
   对向量A=[X,Y,Z]求模：
   $$A_M=[X/(X^2+Y^2+Z^2),Y/(X^2+Y^2+Z^2),X/(X^2+Y^2+Z^2)]$$

scratchN = Cartesian3.normalize(scratchN, scratchN);

9. ScratchN同比例放大一定倍数；
   x轴放大6378137.0 * 6378137.0倍数, Y轴放大6378137.0 * 6378137.0倍数, Z轴放大6356752.3142451793 * 6356752.3142451793倍数，结果放到scratchK中，scratchN保持不变

Cartesian3.multiplyComponents(radiiSquared, scratchN, scratchK)

10. 求经纬度坐标对应的xyz坐标；
    设scratchN向量为$[N_X,N_Y,N_Z]$，放大倍数向量为$[R_X^2,R_Y^2,R_Z^2]$，在cesium中已经定义了$R_X$=6378137，$R_Y$=6378137，$R_Z$=6356752.3142451793，
    则scratchK=$[N_X\ast R_X^2,N_Y\ast R_Y^2,N_Z\ast R_Z^2]$（上一步计算结果）

var gamma = Math.sqrt(Cartesian3.dot(scratchN, scratchK))

该语句执行结果：
$$gamma=\sqrt{N_X^2\ast R_X^2+N_Y^2\ast R_Y^2+N_Z^2\ast R_Z^2}$$

scratchK = Cartesian3.divideByScalar(scratchK, gamma, scratchK);

该语句执行结果:
scratchK向量$N_K=[N_X\ast R_X^2/gamma,N_Y\ast R_Y^2/gamma,N_Y\ast R_X^2/gamma]$
其实就是：$[(N_X\ast R_X/gamma)\ast R_X,(N_Y\ast R_Y/gamma)\ast R_Y,(N_Z\ast R_Z/gamma)\ast R_Z]$
也就是$[N_X\ast R_X,N_Y\ast R_Y,N_Z\ast R_Z]$的模向量$[N_X\ast R_X/gamma,N_Y\ast R_Y/gamma,N_Z\ast R_Z/gamma]$再乘以各个轴对应的放大倍数。

var gamma = Math.sqrt(Cartesian3.dot(scratchN, scratchK));
scratchK = Cartesian3.divideByScalar(scratchK, gamma, scratchK);

回头看到这里的步骤，其实cesium做了两次取模运算，第一次目的是算出经纬度对应的标准球体上面xyz比例，第二次是算出在wgs84坐标系下面进行椭球体拉伸后的xyz比例，最后再用这个拉伸后的比例乘以实际值（以米为单位）算出实际xyz坐标。

11. 求高程对应的xyz坐标增量写入scratchN；

scratchN = Cartesian3.multiplyByScalar(scratchN, height, scratchN)

增量H向量=$[height\ast N_X,height\ast N_Y,height\ast N_Z]$之所以不用第二次拉伸，个人认为是height跟地球半径相比很小，差别可以忽略不计。
如果进行第二次拉伸此处应该是：
增量H向量=$[height\ast (N_X\ast R_X/gamma),height\ast (N_Y\ast R_Y/gamma),height\ast (N_Z\ast R_Z/gamma)]$

12.将第十步骤和第十一步骤对应的坐标相加得到最终xyz值。

return Cartesian3.add(scratchK, scratchN, result)

总结推论：
1）笛卡尔坐标系是米单位;
2）笛卡尔坐标系原点是地球几何中心；
3）xz平面是中央经线和180度经线组成的平面，其中x轴正方向指向的是中央经线，x轴负方向指向180度经线;
4）y轴正方向指向东经90度经线，负方向指向西经90度经线。