Polya定理
一、Burnside引理

二、Polya定理
![]()
![]()
三、应用
简单
题意:n个珠子串成一个项链,用三种颜色去涂色。问一共有多少种不同的涂色方法。经过翻转和旋转得到相同项链的视为相同的涂色方法。
思路:Polya模板题,只是m等于3已给出。
(1)旋转。每次旋转一格,共旋转n次。每次将项链旋转i格后,其循环节数为gcd(n,i)。
(2)翻转。分奇偶讨论。
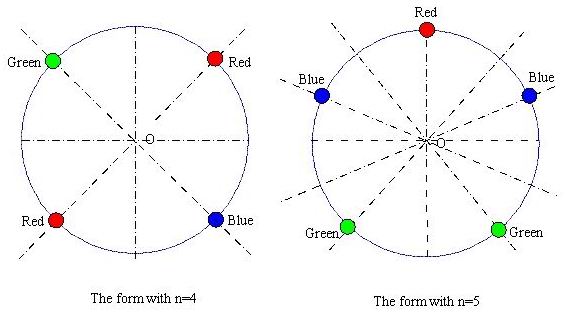
n为奇数时,如图右,对称轴是一个珠子到圆心的连线,一共n条。选定对称轴后,对称轴上的一个珠子构成一个循环,其他n-1个珠子分别以对称轴对称构成(n-1)/2个循环,所以循环节的个数是 1 + (n – 1) / 2 = (n + 1) / 2 。故共有n个循环节数为(n+1)/2的循环群。
n为偶数时,如图左,对称轴可能是两个珠子的连线,一共 n / 2条。选定对称轴后,对称轴上的两个珠子构成两个循环,其他n-2个珠子分别以对称轴对称构成(n-2)/2个循环,循环节个数为2+(n-2)/2=(n+2)2/;对称轴还可能是两个珠子的中点和圆心的连线,所有珠子两两对称,构成n / 2 个循环。 故共有n/2个循环节数为(n+2)/2的循环群,和n/2个循环节数为n/2的循环群。
值得注意的是,旋转加翻转共有2n次置换,故共有2n个置换群,即|G|=2*n.
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int m = 3;
int gcd (int a,int b){
if (b==0)
return a;
return gcd(b,a%b);
}
LL Polya(int n){
LL ret=0;
for(int i=1;i<=n;i++)
ret+=pow(m,gcd(n,i));
if(n&1) ret+=n*pow(m,n/2+1);
else ret+=n/2*(pow(m,n/2)+pow(m,n/2+1));
ret/=2*n;
return ret;
}
int main(){
int n;
while(scanf("%d",&n)&&n!=-1){
if(n==0) puts("0");
else printf("%lld\n",Polya(n));
}
return 0;
} 和上题唯一的不同是m属于输入部分。
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
int gcd (int a,int b){
if (b==0)
return a;
return gcd(b,a%b);
}
LL Polya(int m,int n){
LL ret=0;
for(int i=1;i<=n;i++)
ret+=pow(m,gcd(n,i));
if(n&1) ret+=n*pow(m,n/2+1);
else ret+=n/2*(pow(m,n/2)+pow(m,n/2+1));
ret/=2*n;
return ret;
}
int main(){
int m,n;
while(scanf("%d%d",&m,&n)&&(m&&n)){
printf("%lld\n",Polya(m,n));
}
return 0;
} 题意:n*n的方格棋盘用c种不同的颜色来染色,一共可以得到多少种不同的棋盘。如果一个棋盘,经过任意旋转,反射后变成另一个棋盘,这两个棋盘就是属于同一种棋盘。
思路:旋转和反射共有8种置换(|G|=8),旋转和反射又分奇偶讨论。
旋转有 0,90,180,270度四种旋法。
旋转0度,则置换的循环节数为n*n
旋转90度,n为偶数时,则置换的循环节数为n*n/4,n为奇数,则置换的循环节数为(n*n-1)/4+1
旋转180度,n为偶数时,则置换的循环节数为n*n/2,n为奇数,则置换的循环节数为(n*n-1)/2+1
旋转270度,n为偶数时,则置换的循环节数为n*n/4,n为奇数,则置换的循环节数为(n*n-1)/4+1
反射沿对角反射两种,沿对边中点连线反射两种
n为偶数时,沿对边中点连线反射两种的置换循环节数为 n*n/2,沿对角反射两种的置换循环节数为 (n*n-n)/2+n
n为奇数时,沿对边中点连线反射两种的置换循环节数为 (n*n-n)/2+n,沿对角反射两种的置换循环节数为 (n*n-n)/2+n
注意,结果很大,用java大数解决。
题意:用n种颜色涂立方体六个面的不同种数,能旋转到的算一种。
思路:正方体对应24种不同旋转,即|G|=24。
1.不变置换(1)(2)(3)(4)(5)(6), 共1个;
2.沿对面中心轴旋转 90度, 270度 (1)(2345)(6), (1)(5432)(6) 同类共 6个;
3.沿对面中心轴旋转 180度 (1)(24)(35)(6), 同类共 3个;
4.沿对角线轴旋转 120度, 240度 (152)(346), (251)(643) 同类共 8个;
5.沿对边中点轴旋转 180度 (16)(25)(43) 同类共 6个;
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
int main(){
LL n;//n必须64位,否则WA。算是一个坑点
while(scanf("%lld",&n)&&n){
printf("%lld\n",(n*n*n*n*n*n+3*n*n*n*n+(6+6)*n*n*n+8*n*n)/24);
}
return 0;
} 进阶
UESTC 75
题意:有n种颜色的珠子,给出每种颜色珠子的数量a[i],求能串成多少种不同的项链。能经过旋转得到的相同项链视为同一种项链。
思路:有数量限制的涂色只能用burnside引理。回过头仔细将此题和上面例4.5对比。利用burnside引理,我们要求的就是每个置换(旋转i格)不变元的个数,即每次旋转,所有的涂色方案中有多少涂色方案旋转完还是自身的样子。
根据上面POJ1286知道,每次将项链旋转i格后,其循环节数为gcd(n,i),每个循环节长度为k=n/gcd(n,i)。比如n=6,i=3,那么这个置换表示为(14)(25)(36)。
回到问题上来,一个涂色方案它在某次置换(比如旋转 i 格)中是不是不变元(还是自身的样子)就看它每个循环节里的珠子是不是都是同一种颜色,也就是说14是同一种颜色,25是同一种颜色,36是同一种颜色,只有这样旋转之后才会和原来一样,即是不变元。这就要求每种颜色的珠子数量a[i]必须是k的整数倍,即a[i]%k=0。如果有一个a[i]不满足条件,它就不是不变元。比如上面6颗珠子,如果有两种颜色,分别是2、4,那就可以成为不变元,如果是3、3就不行。
如果都满足a[i]%k=0,接下来就是一个排列组合问题,在一次置换(旋转 i 格)中,总共有n/k=gcd(n,i)个循环节,每种颜色的珠子可以占a[i] / k个循环节,那么第一种颜色的珠子占哪几个循环节就有C(n / k,a[0] / k),第二种就有C( (n-a[0]) / k,a[1] / k),以此类推。这次置换下不变元的数量就是填满所有n/k个循环节的方案数,即C(n / k,a[0] / k)*C( (n-a[0]) / k,a[1] / k)*.......
此题结果太大,用java实现。
//package test;
import java.util.*;
import java.math.*;
public class Main {
static int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
static BigInteger C(BigInteger n,BigInteger m){
BigInteger a=BigInteger.ONE;
if(m==BigInteger.ZERO) return BigInteger.ONE;
for(int i=1; i<=m.intValue(); i++)
a=a.multiply(BigInteger.valueOf(n.intValue()-i+1)).divide(BigInteger.valueOf(i));
return a;
}
public static void main(String[] args) {
final int N = 105;
int a[]= new int[N],b[]=new int[N];
Scanner cin=new Scanner(System.in);
int T=cin.nextInt();
while(T-->0){
int n=cin.nextInt(),sum=0;//n是颜色种数,sum是各颜色总数(珠子数)
for(int i=0;iUVA 10601
题意:给出12条棱的颜色(最多6种颜色),问能组装成多少种立方体。
思路:结合UESTC 75和UVA 10733。
由于颜色数量限制,依旧用Burnside引理。
正方体对应24种不同旋转,即|G|=24。
1、自身不变。循环节12个,每个循环节长度为1。
2、根据对角线为轴旋转120度、240度。循环节4个,每个循环节长度为3。同类置换有4*2个。
3、根据对面的中心连线为轴旋转90、270度。循环节3个,每个循环节长度为4。同类置换有3*2个。
4、根据对面的中心连线为轴旋转180度。循环节6个,每个循环节长度为2。同类置换有3个。
5、根据对边的中心连线为轴旋转180度。循环节7个,5个长度2的循环节、2个长度1的循环节。同类置换有6个。这里要暴力枚举长度为1的循环节涂什么颜色。
#include
#include
#include
#include
#include
typedef long long LL;
using namespace std;
int a[7],b[7];
LL C(int n,int m){
LL a=1;
if(m==0) return 1;
for(int i=1;i<=m;i++) a=a*(n-i+1)/i;
return a;
}
LL count(int k){
int tot=0,i;
for(i=1;i<=6;i++){
if(a[i]%k) return 0;
b[i]=a[i]/k;
tot+=b[i]; // 使得tot最后可以是12/k或10/k
}
LL ret=1;
for(i=1;i<=6;i++){
ret*=C(tot,b[i]);
tot-=b[i];
}
return ret;
}
LL Burnside(){
LL ans = count(1)+6*count(4)+3*count(2)+8*count(3);
//绕对边旋转180°
for(int i=1;i<=6;i++)
for(int j=1;j<=6;j++){
a[i]--;a[j]--; //选定2个颜色,使得函数count()适用于n=10
if(a[i]>=0&&a[j]>=0)
ans+=6*count(2); //虽然选了2个颜色,但用它们涂哪两条边还没定,因此要乘6
a[i]++;a[j]++; //加回来,下个循环还要用
}
return ans/24;
}
int main()
{
int T;
cin>>T;
while(T--){
int t;
memset(a,0,sizeof(a));
for(int i=0;i<12;i++){
scanf("%d",&t);
a[t]++;
}
printf("%lld\n",Burnside());
}
return 0;
} 题意:有3种颜色的珠子,给出每种颜色珠子的数量a[i],求能串成多少种不同的项链。能经过旋转得到的相同项链视为同一种项链。3 ≤sum≤ 40.
思路:结合UESTC 75和POJ 1286。其中在计算总数为偶数时以直径上的两颗珠子为对称轴旋转,要用到上题(UVA 10601)的思想。
#include
#include
#include
#include
#include
#include
typedef long long LL;
using namespace std;
const int n = 3;
int a[n],b[n],sum=0;
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
LL C(int n,int m){
LL a=1;
if(m==0) return 1;
for(int i=1;i<=m;i++) a=a*(n-i+1)/i;
return a;
}
LL Polya(){
LL ans=0;
//旋转
for(int i=0;i=0&&a[j]>=0){
int tot=0,k;
for(k=0;k>T;
while(T--){
sum=0;
for(int i=0;i 题意:n个珠子串成一个项链,用n种颜色去涂色(1<=n<=10^9)。问一共有多少种不同的涂色方法(答案模p)。经过旋转得到相同项链的视为相同的涂色方法。
思路:基本思路就是Polya定理。 ans=[(1/n)*∑n^( gcd(n,i) ]%p。由于n很大,所以需要优化。试想虽然n很大,但是gcd(n,i)的个数必然<=n,如果我们能枚举出gcd值,并计算各个gcd值的个数,那么结果就用到了欧拉函数,如图所示。另外计算n^(d-1)需要用快速幂取模。
#include
#include
#include
#define mst(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long LL;
int euler(int x){
int res = 1;
for (int i = 2; i <= (int)sqrt(double(x)); ++i){
if (x % i == 0){
res *= i-1;
x /= i;
while (x % i == 0){
res *= i;
x /= i;
}
}
}
if (x != 1){
res *= x-1;
}
return res;
}
LL pow(LL a,LL b,LL m){
LL ans=1;
while(b){
if(b&1){
ans=(ans*a)%m;
b--;
}
b/=2;
a=a*a%m;
}
return ans;
}
int main(){
int T;
cin>>T;
while(T--){
int n,p;
scanf("%d%d",&n,&p);
int ans=0;
for(int i=1;i*i<=n;i++){
if(n%i==0){
if(i*i==n) ans=(ans+euler(i)*pow(n,i-1,p))%p; //ans一定要%p
else ans=(ans+euler(n/i)*pow(n,i-1,p)+euler(i)*pow(n,n/i-1,p))%p;
}
}
printf("%d\n",ans);
}
}