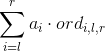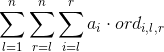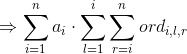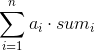[CF1167F]Scalar Queries

Scalar Queries

题解

很明显，可以转化为，其中表示在中排序后的下标。

于是，最后答案为

将提出来，

将后面那一堆记作，答案即为。

也可以表示所有区间中比它小的数的个数，于是关键就变成了如何快速求出的值。

由于只有比小的数才会对的值产生影响，我们设为左边比它小的数的下标集合，为右边比它小的数的下标集合。

可以得到。

为了维护集合与呢，我们想到了线段树。

将数组排序后再一个一个将下标插入到线段树中，求出其的价值和，由于只有比它小的数才会造成影响，所以未插入的数不会产生影响。

源码

#include
using namespace std;
#define MAXN 500005
const int INF=0x7f7f7f7f;
const int mo=1e9+7;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair pii;
uLL n,sum[MAXN<<2],cnt[MAXN<<2],summ;
pii a[MAXN];
uLL querySum(int rt,int l,int r,int al,int ar){
	if(l>r||l>ar||r>1);uLL res=0;
	if(al<=mid)res+=querySum(rt<<1,l,mid,al,ar);
	if(ar>mid)res+=querySum(rt<<1|1,mid+1,r,al,ar);
	return res;
}
uLL queryCnt(int rt,int l,int r,int al,int ar){
	if(l>r||l>ar||r>1);uLL res=0;
	if(al<=mid)res+=queryCnt(rt<<1,l,mid,al,ar);
	if(ar>mid)res+=queryCnt(rt<<1|1,mid+1,r,al,ar);
	return res;
}
void modify(int rt,int l,int r,int ai,LL aw){
	if(l>r)return ;
	if(l==r){sum[rt]=aw;cnt[rt]=1;return ;}
	int mid=l+(r-l>>1);
	if(ai<=mid)modify(rt<<1,l,mid,ai,aw);
	else modify(rt<<1|1,mid+1,r,ai,aw);
	sum[rt]=(sum[rt<<1]+sum[rt<<1|1])%mo;
	cnt[rt]=(cnt[rt<<1]+cnt[rt<<1|1])%mo;
}
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%llu",&a[i].first),a[i].second=i;
	sort(a+1,a+n+1);
	for(int i=1;i<=n;i++){	
		uLL sum1=querySum(1,1,n,1,a[i].second);
		uLL sum2=querySum(1,1,n,a[i].second,n);
		uLL cnt2=queryCnt(1,1,n,a[i].second,n);
		(summ+=(sum1*(n-a[i].second+1)%mo+((n+1)*cnt2+mo-sum2)%mo*a[i].second%mo)*a[i].first%mo)%=mo;
		(summ+=a[i].second*(n-a[i].second+1)%mo*a[i].first)%=mo;
		modify(1,1,n,a[i].second,a[i].second);
	}
	printf("%llu\n",summ);
	return 0;
}

谢谢！！！