JAVA数据结构与算法(六)java实现图
JAVA数据结构与算法(六)java实现图
图的定义
图是由顶点的有穷非空集合和顶点之间边的集合组成,通过表示为G(V,E),其中,G标示一个图,V是图G中顶点的集合,E是图G中边的集合。
无边图:若顶点Vi到Vj之间的边没有方向,则称这条边为无项边(Edge),用序偶对(Vi,Vj)标示。
有向图:若从顶点Vi到Vj的边是有方向的,则成这条边为有向边,也称为弧(Arc)。用有序对(Vi,Vj)标示,Vi称为弧尾,Vj称为弧头。如果任意两条边之间都是有向的,则称该图为有向图。
有向图G2中,G2=(V2,{E2}),顶点集合(A,B,C,D),弧集合E2={
权(Weight):有些图的边和弧有相关的数,这个数叫做权(Weight)。这些带权的图通常称为网(Network)。
图的搜索:
深度优先遍历:也有称为深度优先搜索,简称DFS。其实,就像是一棵树的前序遍历。它从图中某个结点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有 路径相通的顶点都被访问到。若图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中的所有顶点都被访问到为止。
基本实现思想:
(1)访问顶点v;
(2)从v的未被访问的邻接点中选取一个顶点w,从w出发进行深度优先遍历;
(3)重复上述两步,直至图中所有和v有路径相通的顶点都被访问到。
广度优先遍历:也称广度优先搜索,简称BFS。BFS算法是一个分层搜索的过程,和树的层序遍历算法类同,它也需要一个队列以保持遍历过的顶点顺序,以便按出队的顺序再去访问这些顶点的邻接顶点。
基本实现思想:
(1)顶点v入队列。
(2)当队列非空时则继续执行,否则算法结束。
(3)出队列取得队头顶点v;访问顶点v并标记顶点v已被访问。
(4)查找顶点v的第一个邻接顶点col。
(5)若v的邻接顶点col未被访问过的,则col入队列。
(6)继续查找顶点v的另一个新的邻接顶点col,转到步骤(5)。
直到顶点v的所有未被访问过的邻接点处理完。转到步骤(2)。
广度优先遍历图是以顶点v为起始点,由近至远,依次访问和v有路径相通而且路径长度为1,2,……的顶点。为了使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问,需设置队列存储访问的顶点。
普利姆算法(Prim):从连通的图挨着找权最小的
克鲁斯卡尔算法(Kruskal):从全图找权最小的满足的
什么是度:

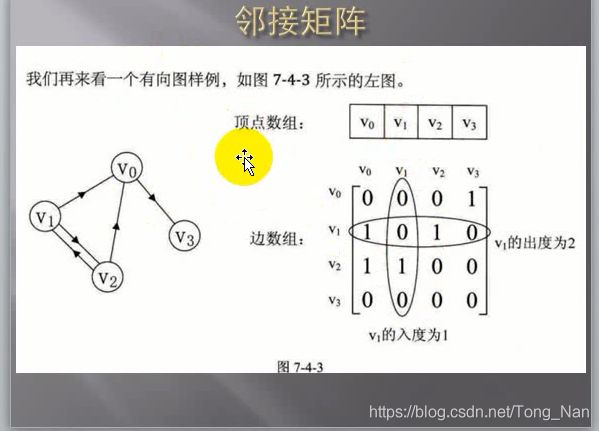
图的邻接矩阵:
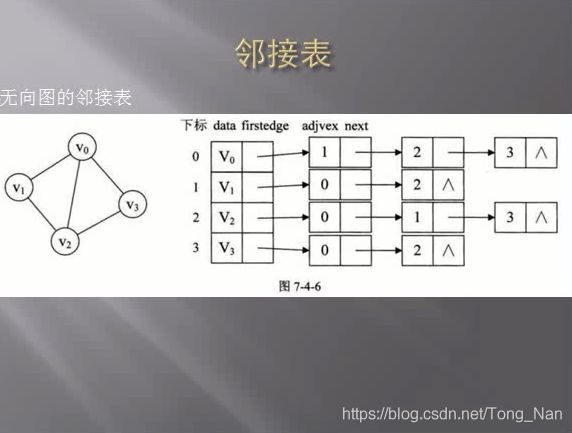
无向图邻接表:
有向图邻接表 :
图顶点的出度和入度查找和权值,代码如下:
public class Graph {
private int vertexSize; //顶点数量
private int[] vertexs; //顶点数组
private int[][] matrix; //连接矩阵
private final static int MAX_WEIGHT=1000;//最大权值
public Graph(int vertexSize){
this.vertexSize=vertexSize;
matrix=new int[vertexSize][vertexSize];
vertexs=new int[vertexSize];
for(int i=0;i<vertexSize;i++){
vertexs[i]=i;
}
}
//获取某个顶点的出度
public int getOutDegree(int index){
int degree=0;
for(int j=0;j<matrix[index].length;j++){
int weight=matrix[index][j];
if(weight!=0&&weight!=MAX_WEIGHT){
degree++;
}
}
return degree;
}
//获取某个顶点的入度
public int getInDegree(int index){
int degree=0;
for(int i=0;i<matrix.length;i++){
int weight=matrix[i][index];
if(weight!=0&&weight!=MAX_WEIGHT){
degree++;
}
}
return degree;
}
//获取某个顶点之间的权值
public int getWeight(int v1,int v2){
int weight=matrix[v1][v2];
return weight==0?0:(weight==MAX_WEIGHT?-1:weight);
}
public int[] getVertexs() {
return vertexs;
}
public void setVertexs(int[] vertexs) {
this.vertexs = vertexs;
}
public static void main(String[] args) {
Graph graph=new Graph(5);
int [] a1=new int[]{0,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,6};
int [] a2=new int[]{9,0,3,MAX_WEIGHT,MAX_WEIGHT};
int [] a3=new int[]{2,MAX_WEIGHT,0,5,6};
int [] a4=new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,0,1};
int [] a5=new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,0};
graph.matrix[0]=a1;
graph.matrix[1]=a2;
graph.matrix[2]=a3;
graph.matrix[3]=a4;
graph.matrix[4]=a5;
int outdegree=graph.getOutDegree(0);
System.out.println("V0出度为:"+outdegree);
int indegree=graph.getInDegree(0);
System.out.println("V0的入度:"+indegree);
int weight=graph.getWeight(0, 4);
System.out.println("v0到v4的权值为:"+weight);
}
}
图的广度优先算法和深度优先算法
public class Graph {
private int vertexSize; //顶点数量
private int[] vertexs; //顶点数组
private int[][] matrix; //连接矩阵
private final static int MAX_WEIGHT=1000;//最大权值
private boolean[] isVisited;
public Graph(int vertexSize){
this.vertexSize=vertexSize;
matrix=new int[vertexSize][vertexSize];
vertexs=new int[vertexSize];
for(int i=0;i<vertexSize;i++){
vertexs[i]=i;
}
isVisited=new boolean[vertexSize];
}
//获取某个顶点的第一个邻接点
public int getFirstNeighbor(int index){
for(int j=0;j<vertexSize;j++){
if(matrix[index][j]>0&&matrix[index][j]<MAX_WEIGHT){
return j;
}
}
return -1;
}
//根据前一个邻接点获取下个邻接点 V是要找的点,index上一个点的下标
public int getNextNeighbor(int v,int index){
for(int j=index+1;j<vertexSize;j++){
if(matrix[v][j]>0&&matrix[v][j]<MAX_WEIGHT){
return j;
}
}
return -1;
}
//图的深度优先遍历算法
public void depthFirstSearch(int i){
isVisited[i]=true;
int first=getFirstNeighbor(i);
while(first!=-1){
if(!isVisited[first]){
//需要遍历该顶点
System.out.println("访问到了:"+first+"顶点");
depthFirstSearch(first);
}
first=getNextNeighbor(i, first);//第一个相对first的邻接点
}
}
//对外公开的深度优先遍历
public void depthFirstSearch(){
isVisited=new boolean[vertexSize];
for(int i=0;i<vertexSize;i++){
if(!isVisited[i]){
System.out.println("访问到了:"+i+"顶点");
depthFirstSearch(i);
}
}
isVisited=new boolean[vertexSize];
}
/*
* 图的广度优先搜索算法
*/
public void broadFirstSearch(int i){
int u,w;
LinkedList<Integer> queue=new LinkedList<Integer>();
System.out.println("访问到:"+i+"顶点");
isVisited[i]=true;
queue.add(i);//第一次把V0加入队列
while(!queue.isEmpty()){
u=(Integer)queue.removeFirst().intValue();
w=getFirstNeighbor(u);
while(w!=-1){
if(!isVisited[w]){
System.out.println("访问到:"+i+"顶点");
isVisited[w]=true;
queue.add(w);
}
w=getNextNeighbor(u, w);
}
}
}
//对外公开的广度优先算法
public void broadFirstSearch(){
isVisited=new boolean[vertexSize];
for(int i=0;i<vertexSize;i++){
if(!isVisited[i]){
broadFirstSearch(i);
}
}
}
public static void main(String[] args) {
Graph graph=new Graph(9);
int [] a1=new int[]{0,10,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,11,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT};
int [] a2=new int[]{10,0,18,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,16,MAX_WEIGHT,12};
int [] a3=new int[]{MAX_WEIGHT,MAX_WEIGHT,0,22,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,8};
int [] a4=new int[]{MAX_WEIGHT,MAX_WEIGHT,22,0,20,MAX_WEIGHT,MAX_WEIGHT,16,21};
int [] a5=new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,20,0,26,MAX_WEIGHT,7,MAX_WEIGHT};
int [] a6=new int[]{11,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,26,0,17,MAX_WEIGHT,MAX_WEIGHT};
int [] a7=new int[]{MAX_WEIGHT,16,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,17,0,19,MAX_WEIGHT};
int [] a8=new int[]{MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,16,7,MAX_WEIGHT,19,0,MAX_WEIGHT};
int [] a9=new int[]{MAX_WEIGHT,12,8,21,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,MAX_WEIGHT,0};
graph.matrix[0]=a1;
graph.matrix[1]=a2;
graph.matrix[2]=a3;
graph.matrix[3]=a4;
graph.matrix[4]=a5;
graph.matrix[5]=a6;
graph.matrix[6]=a7;
graph.matrix[7]=a8;
graph.matrix[8]=a9;
graph.depthFirstSearch();
//graph.broadFirstSearch();
}
}