立体匹配——DP动态规划算法

动态规划算法原理：
（1）https://www.bilibili.com/video/av16544031/?spm_id_from=333.788.videocard.1
（2）https://www.bilibili.com/video/BV12W411v7rd/?spm_id_from=333.788.videocard.0
动态规划立体匹配原理：https://www.bilibili.com/video/BV1ax411R7Hd?p=22
动态规划立体匹配参考博客：https://blog.csdn.net/He3he3he/article/details/103599445
动态规划立体匹配参考论文：《基于动态规划的立体匹配算法研究》

（1）DP立体匹配原理：

（2）DP算法求最优路径代码实现：

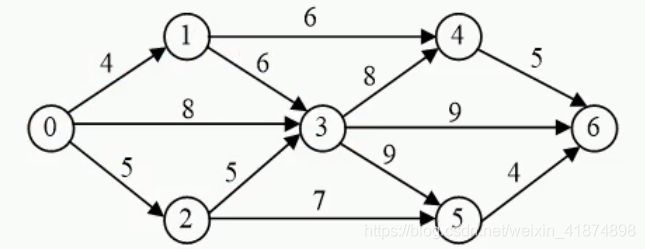
如上图所示，求结点0到结点6的最短路径。
算法设计：为计算0-6之间的最短路径，只需要依次计算出0到各中间结点的最短路径。
其中：若结点K经过从结点0到结点6的最短路径，则这条路径中从0到k之间的部分也是0到k的最短路径。

#if 0
#include
#define n 7
#define x 9999

int map[n][n]=
{
	{x,4,5,8,x,x,x},
	{x,x,x,6,6,x,x},
	{x,x,x,5,x,7,x},
	{x,x,x,x,8,9,9},
	{x,x,x,x,x,x,5},
	{x,x,x,x,x,x,4},
	{x,x,x,x,x,x,x}
};

int main()
{
	int cost[n];	//第0点到结点i所需要的最小cost
	int path[n] = {0};	//从结点0到结点i的最短路径上i的上一个点
	for (int i = 1; i < n; i++)
	{
		cost[0] = 0;
		int Minval = x;
		for (int j = 0; j < i; j++)
		{
			printf("%d\t", cost[j]);
			printf("%d\t", map[j][i]);
			if (map[j][i] != x)
			{
				if ((cost[j]+map[j][i])<Minval)
				{
					Minval = cost[j] + map[j][i];
					printf("%d\t", Minval);
					path[i] = j;
				}
			}
		}
		printf("%d\n", path[i]);
		cost[i] = Minval;
	}

	printf("____________________");
	//最短路径cost
	printf("%d\n", cost[n - 1]);
	//最短路径path
	int i = n - 1;
	while (i!= 0)
	{
		printf("%d ", path[i]);
		i=path[i];
	}

	return 0;
}
#endif // 1

（3）DP算法立体匹配代码实现：

代码下载链接：https://download.csdn.net/download/weixin_41874898/12493721

注意：
（1）代码中的图片大小是固定了一个值，如果要更改不同图片，对应需要更改大小
（2）必须是bmp格式图片（更改bmp文件格式不是更改后缀，需要将用画图软件打开保存为bmp格式）
（3）代码中是先做行优化，再做列优化，效果如下：

• a）只做行方向优化：
  
• b）做行方向+做列方向优化：