【数字图像处理】LeetCode与图像处理(连通域的计算)
基本概念
在数字图像处理中,有个连通域的概念
连通区域(Connected Component)一般是指图像中具有相同像素值且位置相邻的前景像素点组成的图像区域(Region,Blob)。
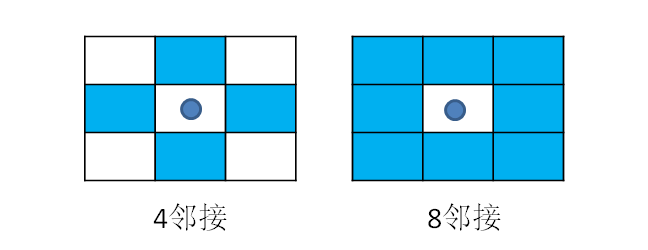
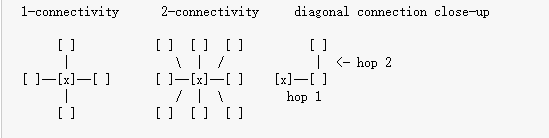
在图像中,最小的单位是像素,每个像素周围有 8 个邻接像素,常见的邻接关系有 2 种:4 邻接与 8 邻接。4 邻接一共 4 个点,即上下左右、8 邻接的点一共有 8 个,包括了对角线位置的点,如下图所示
二值图(图上的值只有 0 和 1,或者 0 和 255)是非常常用的一种图像,我们可以用它来寻找目标的轮廓,形状识别等操作,同时,我们也利用二值图来寻找一个图像的连通域。如下图,就是一个很直观的连通域图,图中总共有 6 个连通域。

寻找连通域的方法
OpenCV 库
在 OpenCV 中,提供了一个函数 cv2.connectedComponentsWithStats 可以帮助我们计算连通域的一些信息,其接口说明如下:
connectedComponentsWithStats(image[, labels[, stats[, centroids[, connectivity[, ltype]]]]]) -> retval, labels, stats, centroids
image:输入的图像,必须是单通道 8-bit 的图像
labels:一张和输入图像大小一样的掩膜(mask),对于相同的连通域,使用同一个标号进行标记,背景标记为 0
stats:记录了连通域的一些信息
centroids 连通域的质心
connectivity:4 或者 8, 使用 4 连通域还是 8 连通域
ltype:输入 labels 的数据类型,CV_32S 或者 CV_16U
下图是一个图像得到的连通域掩膜,即上面提到的 labels 输出

为了方便起见,我们构建一张图来测试我们的程序
import cv2
import numpy as np
# 创建一个黑色的画布
img = np.zeros((516, 512), np.uint8)
# 绘制长方形,起始和终点坐标,颜色,厚度
img = cv2.rectangle(img, (10, 10), (49, 49), (255), -1)
# 绘制圆形,给定圆心,半径,最后 -1 为图形填充
img = cv2.circle(img, (180, 88), 50, (255), -1)
# 绘制椭圆,椭圆心,长轴,短轴,角度,起始结束角,填充
img = cv2.ellipse(img, (256, 256), (100, 50), 0, 0, 360, 255, -1)
retval, labels_cv, stats, centroids = cv2.connectedComponentsWithStats(img, ltype=cv2.CV_32S)
# cv2.imshow("labels", labels)
cv2.imshow("img", img)
k = cv2.waitKey(0) & 0xFF
if k == 27:
cv2.destroyAllWindows()
在该图中,我们绘制了 3 个图像,正方形、圆形、椭圆形,其中正方形的面积是 40×40=1600,圆形的质心是 (188, 88),请记住这些值,下面会对其进行说明。

我们重点对输出的 stats 和 centroids 进行观察
stats
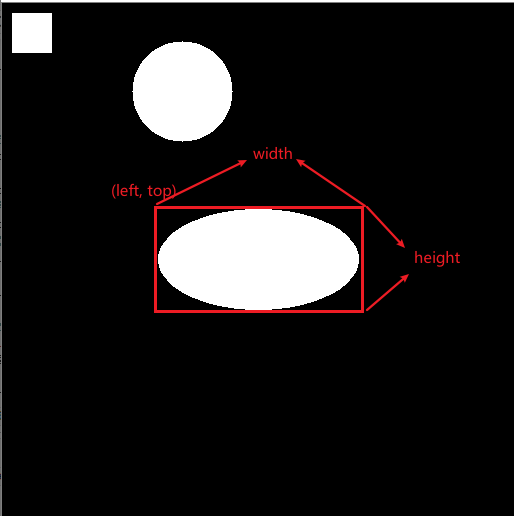
stats 是一个 (label, 5) 的矩阵,label 是连通域的个数(包括背景) [left, top, width, height, area] 分别是连通域左上角的坐标,连通域的宽、高、以及面积
这个图可以帮助理解
centroids
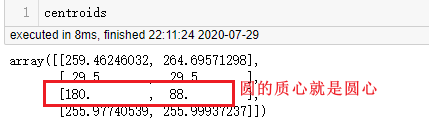
centroids 是连通域的质心,圆形的质心就是圆心,很好理解
skimage 库
skimage 库中也有一个与 OpenCV 版本一样的函数 skimag.measure.label ,其接口如下
labels, num = measure.label(input, neighbors=None, background=None, return_num=False, connectivity=None)
input:输入的图像
neighbors:1 对应的是 4 邻接,2 对应的是 8 邻接
return_num:是否返回连通域的数量,否的话,该函数只有一个输出 labels
labels:同 OpenCV 的输出,但是可能索引值的顺序会不一样
num:连通域的数量,不包括背景,与 OpenCV 的区别
import cv2
import numpy as np
from skimage import measure
# 创建一个黑色的画布
img = np.zeros((516, 512), np.uint8)
# 绘制长方形,起始和终点坐标,颜色,厚度
img = cv2.rectangle(img, (10, 10), (49, 49), (255), -1)
# 绘制圆形,给定圆心,半径,最后 -1 为图形填充
img = cv2.circle(img, (180, 88), 50, (255), -1)
# 绘制椭圆,椭圆心,长轴,短轴,角度,起始结束角,填充
img = cv2.ellipse(img, (256, 256), (100, 50), 0, 0, 360, 255, -1)
labels, num = measure.label(img, return_num=True) # num =3 不包括背景
# cv2.imshow("labels", labels)
cv2.imshow("img", img)
k = cv2.waitKey(0) & 0xFF
if k == 27:
cv2.destroyAllWindows()
LeetCode 与图像处理
有读者会问,LeetCode 怎么会和图像处理扯上关系呢,还真有
LeetCode 上的题目是:200:岛屿数量 https://leetcode-cn.com/problems/number-of-islands/,具体描述如下,这道题跟我们今天所讲的图像连通域有非常相似之处,个人猜想,上面两种库的实现应该与下面的实现思路是类似的。
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
[
['1','1','1','1','0'],
['1','1','0','1','0'],
['1','1','0','0','0'],
['0','0','0','0','0']
]
输出: 1
示例 2:
输入:
[
['1','1','0','0','0'],
['1','1','0','0','0'],
['0','0','1','0','0'],
['0','0','0','1','1']
]
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
这里简单说一下解题思路,就是利用广度优先搜索,即遍历所有像素,看看该像素上下左右的值是否和该像素一样(我们假设是二值图像,并且是 4 连通的),若是的话,将其压入队列中,同时将其标记为已访问。
我们使用和上面一样的测试用例,编写程序如下
from collections import deque
import cv2
import numpy as np
from skimage import measure
# 创建一个黑色的画布
img = np.zeros((516, 512), np.uint8)
# 绘制长方形,起始和终点坐标,颜色,厚度
img = cv2.rectangle(img, (10, 10), (49, 49), (255), -1)
# 绘制圆形,给定圆心,半径,最后 -1 为图形填充
img = cv2.circle(img, (180, 88), 50, (255), -1)
# 绘制椭圆,椭圆心,长轴,短轴,角度,起始结束角,填充
img = cv2.ellipse(img, (256, 256), (100, 50), 0, 0, 360, 255, -1)
class Solution:
def numIslands(self, grid: np.array) -> int:
high = len(grid)
# 特殊处理,当矩阵为空
if high == 0:
return 0
width = len(grid[0])
print(high, width)
queue = deque()
num = 0
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)] # 四个方向的偏移
for i in range(high):
for j in range(width):
# 岛屿,且没有被访问过,BFS搜索
if grid[i, j] == 255: # 为了直观展示,我们将陆地记为 255,海洋记为 0
queue.append((i, j)) # 把点放进队列中
grid[i, j] = 254 # 访问过的点记为 254
while queue:
x, y = queue.popleft()
# 判断当前点的上下左右是否是陆地且未被访问过的,是的话入队
for d in directions:
cur_x = x + d[0]
cur_y = y + d[1]
if 0 <= cur_x 喜欢的朋友给个三连哈~~
![]()
![]()
机器视觉 CV
与你分享 AI 和 CV 的乐趣
分享数据集、电子书、免费GPU
长按二维码关注我们