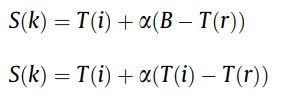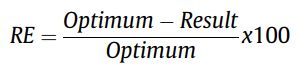多目标优化 MOP （九）：Tree-Seed algorithm 2019

论文：A discrete tree-seed algorithm for solving symmetric traveling salesman problem

TSP问题可以通过exact menthods和heuristic method解决。

exact menthods包括e branch and bound , branch and cut , branch and price , cutting planes ， Lagrangian dual等。

heuristic method包括ABC，PSO，SA，ACO，neural network，tabu search，artificial immune systems，cuckoo search, black hole (BH) , STA , fruit fly ， imperialist competitive algorithm (ICA), physarum-energy optimization (PEO) 和 GA等。

解决permutation coded optimization problems由两种方法，path construction 和 path improvement。path construction是采用problem information去生成新的solutions，path improvement通过crossover，mutation和swap生成新的solutions。通常，path improvement不利用problem information使用较少的时间生成候选集candidate solution，但是需要迭代很多次获得一个高质量的解。本文的只在生成候选集的时候使用information，初始化算法时候一个solution通过悬着最近的nodes分配给一个tree，以改善DTSA的收敛性。对于其他的trees，随机生成permutatuion solutions。当满足终止条件时，solution由2-opt algorithm改进。2-opt algorithm是一种local search 技术可以增强solution的质量。

metaheuristic algorithms元启发式算法产生候选集有三个阶段：初始化，交叉和变异。

对于permutation-coded path 编码问题，初始化可以通过random permutation 或者 nearest neighbor tour construction heuristic两种方式产生。

1）关于 evolutionary computation 和 swarm intelligence methods的研究

crossover交叉方式：

1. partially-mapped crossover (PMX) 1985  
2. Heuristic Crossover (HX)，效果并不好
3. order crossover (OX) 1985 论文地址
4. cycle crossover (CX)  1987
5. Inver-over 1998
6. CX2 2017：CX2在一些问题上比PMX好，一些没有PMX好，但是大部分比OX好
7. order based crossover (OBX)  1990
8. position-based crossover (PBX)  1990
9. Subtour Exchange Crossover
10. Enhanced edge recombination crossover (ERX) 1991
11. generalized N-point crossover (GNX) 1995
12. 2-opt and Lin-Kernighan local search methods，Lin-Kernighan效果更好
13. sorted match crossover (SMX) 
14. maximal preservative crossover (MPX)
15. alternating position crossover (APX)
16. voting recombination crossover (VRX)
17. DPSO中的delete-crossover process
18. sequential constructive crossover（SCX）,在Tsymmetric and asymmetric TSPLIB问题中，SCX比ERX,GNX效果好

变异方法：

1. swap
2. swap sequence mutation
3. local hillclimbing
4. scramble techniques
5. exchange mutation (EM)
6. inversion mutation (IVM)
7. displacement mutation (DM)
8. insertion mutation (ISM)
9. simple inversion (SIM)
10. scramble mutation (SM)
11. DPSO中的slide and reverse operators
12. Greedy Sub Tour Mutation (GSTM)
13. neighborhood operators (RS, RI, RSS, RIS, RRS, RRSS, RRIS)
14. transformation operators

Larranaga 对TSP问题进行了不同的编码如 binary, path, adjacency, ordinal and matrix，对不同的交叉，变异方式在3个TSP问题上进行了测试，发现ERX比其他交叉操作更好，不同的变异操作没有明显差异，TSP最好的编码方式是path。

discrete artificial bee colony algorithm 生成候选集的方法有：

swapping group

1. Random Swap (RS)
2. Random Reversing Swap of Subsequences (RRSS)
3. Random Reversing of Subsequence (RRS)
4. Random Swap of Subsequences (RSS)

insertion group

1. Random Insertion of Subsequence (RIS)
2. Random Insertion (RI)
3. Random Reversing Insertion of Subsequence (RRIS) operators

local edge exchange启发方法有：

1. 2-opt
2. or-opt
3. double bridge
4. Lin and Kernighan neighborhoods

PACO-3Opt 算法采用了 3-opt local search algorithm 由于局部搜索非常耗费时间因此该算法采用了 parallelization 。这个算法克服了ACO过早收敛的缺点。

选择方法：

1. Stochastic Universal Selection (SUS)
2. Rank Selection (RS)
3. Tournament Selection
4. Roulette Wheel Selection (RWS)
5. enhanced parent selection 使用minimum distance knowledge，与RS相似但是不用排序

Tree-Seed Algorithm (TSA) 2015年提出，用于解决连续优化问题的population-based算法，以往的文献中多用于解决基于约束的和二进制的TSP问题，这篇文章对决策变量是整数的discrete TSA（DTSA）的问题进行了研究。DTSA是用于permutation-coded 问题的新颖的和交互的离散优化算法。

这篇文章对TSA的几个参数进行了研究：search tendency, number of seeds, number of trees。

下面介绍一下TSA的原理：trees and seeds表示可能的solutions，初始化阶段，trees随机生成，trees的数量称为stand size，seeds数量在10%-20% stand size之间，seeds通过下面的公式生成

T(i) 是 第i个 tree, S(k) 是T(i)第k个seed , a 是- 1 和 1之间均匀分布的随机数, B 是目前得到最好的tree, T(r) 是与 T (i)不同的一颗随机tree。这两个生成seeds的公式由Search Tendency (ST) parameter控制，参数在[0,1]取值，在搜索过程中，一个在[0,1]均匀分布的随机数生成了，并与ST进行比较，如果ST小于随机数，执行第一个公式，否则执行第二个。公式1提高了收敛性，公式2提供了多样性。

discrete tree-seed algorithm (DTSA):

初始化时，随机生成permuttations trees和一个最近邻tour被分配给一个tree，在DTSA中使用Transformation operators生成seeds而不是上面的两个公式。当满足结束条件后，得到的solution应用2-opt 算法进行更新。

Transformation operators：seeds生成的方法有swap, shift and symmetry。seeds是在可行域空间中生成的，因此不需要修复机制。

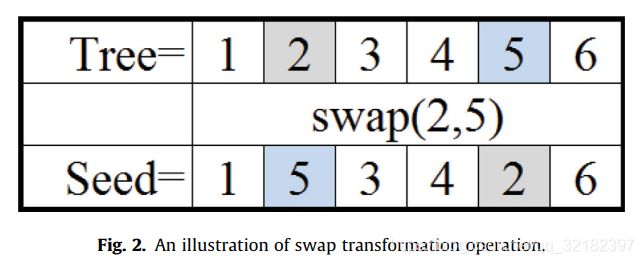
1. Swap transformation:随机生成2个[0,N]之间是数字，N是决策变量的总数，tree中的两位位置被调换生成心的seed，Swap transformation是对tree的小的改动 
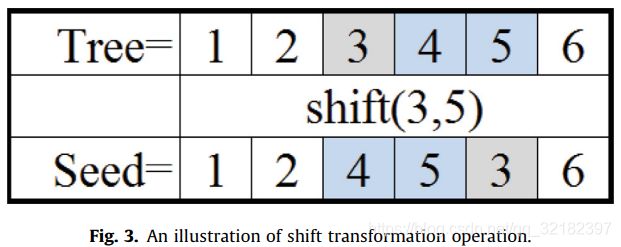
2. shift transformation：首先随机生成2个[0,N]之间是数字x，y，N是决策变量的总数。x的位置被标记，x右侧到y位置的决策变量移动到左侧，x移动到y的位置。这种方式是中等的变化，比上面的方法变动大。
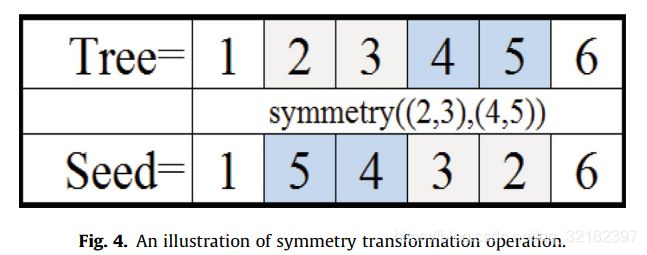
3. Symmetry transformation：生成两个随机的位置的block，每个block中的元素反转，然后blocks交换。这种方式的变化很大。

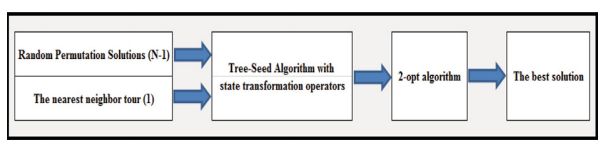
DTSA算法框架：

首先初始化生成根据最近邻tour一个solution，再生成N-1个随机permutation solution，然后将TSA算法与swap，shift，symmetry transformation operators混合进行迭代，当满足结束条件后，得到的solution应用2-opt 算法进行更新。

测试TSP问题，指标采用relative error (RE)

Experiment 1: Comparisons of transformation operators for TSP

symmetry operator获得了最好的结果，因为提供了更大的多样性

Experiment 2: determining the N and ST parameters for DTSA

trees (N)设置为10–300 ，step为10，N的取值影响不大。ST取值为0.1-0.9，step=0.1，影响也不大，最后取ST=0.5。seeds (NS)设置为6。