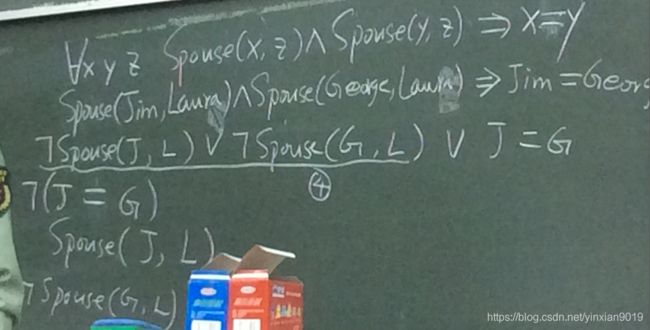《人工智能》 第八章
一阶逻辑的语法及语义
模型 解释
命题逻辑里面的模型是:
======

一阶逻辑里面语句的符号:
一阶逻辑里面可能元素有哪些东西?
一阶逻辑的可能世界里面, 包含对象, 关系元素。
要定义一阶逻辑的模型, 回到上诉三个问题, 左边有什么?右边有什么?
FOL一阶逻辑的模型
- 包含对象
- 对象之间有关系 , 关系使用元组形式表示, 还有函数。
FOL逻辑的符号

个体常元: 可能世界里面具体的对象
谓词:用来讲关系 ,用谓词描述关系
函词: 函数,
函词和谓词之间有时候可以转换,又有区别,比如例子:

一阶函数的模型, 包含一组对象, 以及一个解释。


:两个。
因为右边已经固定了 ,由前三行确定 。 其实这就是问有多少种解释, 右边固定了, 左边也固定了 ,问有多少种解释。
首先, mother谓词智能解释成关系 mother{a,b} , 这两个常量符号 sucie , bob , 都既可以解释成a 也可以解释成b.
这样的模型, 有多少个可能的模型, 就是说解释有4个, 就有4个可能的模型。
下一个例子:

命题逻辑里面讲过蕴含: P(A),P(B) 蕴含? 任意x P(X), 右边这条语句在所有使得左边为真的情况(模型)下都为真。
如果说蕴含不成立,需要找到一个反例, 这个模型使得左边为真, 右边为假, 现在尝试找到这样一个模型, 要找到一个反例的模型, 首先要说清楚 ,对象集合是什么。?
假设对象集合里面有三个对象, 其中, a 和b 解释成三个对象中的两个。
找不到, 所以就得不出 任意x P(X)这样的结论。
讲蕴含的时候讲过若干种方法:
1、 模型检验
2、逻辑等价
3、推理规则

先看模型检验: 思想是, 把所有模型枚举出来, 在每一个模型下都成立
在命题逻辑里面可以枚举, 但是一阶逻辑里面不行, 因为模型太大。
例如, 模型域里面有6个对象, 语句有两个常量, 1个二元关系。
对象为1, 的情况, 有两个常量, 只能解释到同一个对象 , 圆圈外面是逻辑语句。 对象自己和自己是没有关系的。
3)如果对象集合里面有两个对象, 可以看里面到底有多少个模型?

这些模型的数量为2 的时候 4 。
什么是项: 常量符号, 对象, 变量, 项在映射的左边,对象在映射的右边
复合语句是 原子语句用逻辑连接词连在一起。
全称量词 与 存在量词
逻辑连接词 : 
如何确定存在量词 和全称量词的真值

假设对象集合有两个对象, 这条语句消去全称量词 , 它等于什么? 等价于 把 John 带入得到一条语句, Micheal 带入得到一条语句, 合在一起。

通常蕴含量词 , 是和 全称量词一起用, 存在量词和合取一起用。
存在量词和全称量词之间有关系。

1) 两个全称量词 x , y , 交换是否正确 ,如果把x, y , 看做坐标轴, 所以这二者是同一件事情。
2) 存在x , 存在y , 是相同的, 表达意思一致。
3) 不是相同的, 例如, 任意x存在y , 和 存在x 任意y , 前者, 任何人都存在mother , 存在x , 是任何人的mother 。
也就是两个连续的全称量词和存在量词的顺序是可以交换的, 但是存在量词和全称量词连续不可交换。
全称量词和存在量词之间可以相互转换:在全称量词和存在量词前面各加一个否定。
表示两个项指代同一对象
项: 常量、变量、函数(函词)
这就是讲的, R J 两个项指代同一个对象 : 、
使用等词描述, 比如Father (John) = Henry , Father , Henry 都被解释为一个对象。
解释为同一个对象。
Richard , 有两个兄弟 , 两个兄弟x,y , 存在x, y, 使得 X是Richard 是兄弟, Y 和Richard 是兄弟, X he Y 可以解释为同一个人, 如果X和Y 指代为同一个对象, Richard 就是一个兄弟, 所以要加上 X,Y不相等。

如果去掉At least , 就是说现在 , Richard 只有两个兄弟, 如何描述?


有一个办法可以降低这个的复杂程度 , 需要设计一种新的语义 ,这个是在一阶逻辑的语义下表示的 , 现在用一种新的语义: 数据库语义。
没有出现的原子语句 , 知识库里面没有讲到的, 都为假, 这个假设被称为, 封闭世界假设。
就是说有多少个常量符号 就有多少个对象。
这三个约定下面, 这样的语义称为数据库语义。
这个数据库语义和一阶逻辑的语义明显不同, 此时, 每个常量符号指代不同的对象, John , Richard , Geoffrey, Richard 。
这里面只出现了三个常量符号, 总共就三个对象。
其他没有出现的语句都为假, 都没出现。
使用一阶逻辑

讲命题逻辑是, 对知识库的操作有 TELL ASK ,
一阶逻辑里面多了ASKVARS : 什么样的X使得ASKVARS 为真?
亲属关系域

如果对母亲下定义, 这里面的逻辑连接词是什么?注意Mother 是一个函数 , female , 和parent , 都是二元谓词。
会不会用到等词?mother 是一个函数, 函数的结果是一个什么东西?

注意, 开始确定什么作为一元谓词, 二元谓词, 函数, 是我们自己规定的。

husband 是谓词, 指的是, h 是male , h 是w 的Spouse .



前面的一些公式是定义, 公理, 有时候对于一些概念无法进行准确的定义, 比如我们不需要对person 进行完整的定义, 但是我们应该写出每个人都具有的属性。
如果说X是一个人, 那么他具备哪些属性?
或者说, X满足什么条件后, 他是一个人。
在这样的定义下, 右边的属性比双向蕴含的属性要少, 反过来再第二行, 这里面的约定比双向蕴含的条件要多一些 。
公理放到知识库里面, 在知识库里面加上公理, 得不到期望的答案, 这说明了, 知识库里面的公理不充分。
自然数

1、 0 是自然数
2、如果N是自然数, 那么N的后继也是自然数 。
需要对后继函数约束。
3、任何函数的后继都不等于0
4、 N不等于m , 那么他们的后继也不一样
我们使用后继函数定义加法, m 是自然数, n 是自然数, m 的后继加上n = m + N 的后继。
5、 加号写到前面, 可以使用中缀表示法:

对自然数的定义, 可以
跳过 Set
练习 8.3 8.4

什么叫有效? 那么这条语句是否在每一个模型下都为真呢? 这里的等号, 在前面讲, 指代统一的对象。
8.4 把上面的语句改成全称量词。
可以加入一个常量带入, ba x y z 分别替换成一个常量, 由这个语句可以得到什么呢?
可以得到非
b. Joe 是个演员, 但他还有另外一个工作。