【cpg控制】Hopf振荡器的一种python实现
hopf实现
- 一、python 解微分方程
- 1、利用dsolve求解析解
- 2、利用scipy.integrate.odeint求解
- 二、hopf振荡器实现
- 1、numpy
- 2、odeint
一、python 解微分方程
python有用于求解常微分方程的库,库里面提供了不少功能,例如sympy的dsolve,以及scipy.integrate.odeint。其具体用法可参考官方文档,这里就不过多赘述,举两个例子看下效果
1、利用dsolve求解析解
f ( x ) ′ ′ + f ( x ) = 0 {f(x)}'' + f(x) = 0 f(x)′′+f(x)=0
import sympy as sy
def fun(x,f):
return sy.diff(f(x),x,2)+f(x)
x=sy.symbols('x') # 变量符号
f=sy.Function('f') # 函数符号
sy.pprint(sy.dsolve(fun(x,f),f(x))) # 打印等式
我们能得到以下方程
f(x) = C₁⋅sin(x) + C₂⋅cos(x)
取 c 1 = 1 , c 2 = 1 c_1=1, c_2=1 c1=1,c2=1,我们用matplotlab把他的图像画出来:
t = np.arange(0, 5, 0.001)
y = np.sin(t) + np.cos(t)
figure = plt.figure()
plt.grid(ls="--")
plt.plot(t, y)
plt.show()

2、利用scipy.integrate.odeint求解
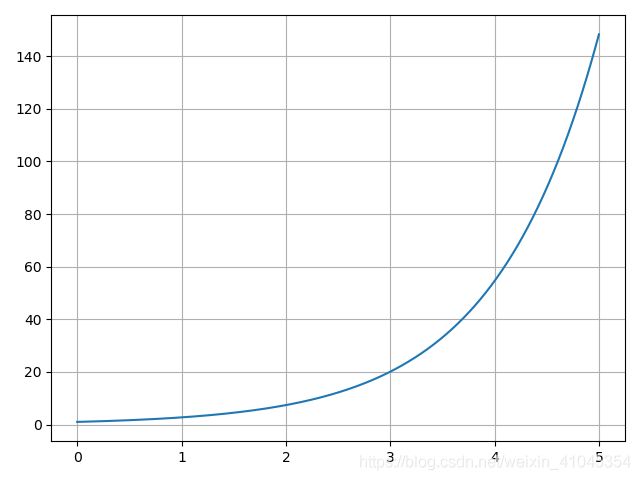
我们先尝试一阶的微分方程: d y d t = y \frac{dy}{dt} = y dtdy=y,这条微分方程我们手动算的话很容易的出 y = c e x y=ce^x y=cex,注意使用odeint的话,微分方程必须化成标准形式,fun函数必须返回dy。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def fun(y, t):
return np.array(y)
t = np.arange(0, 5, 0.001)
result = odeint(fun, 1, t)
plt.plot(t, result[:, 0])
plt.grid()
plt.show()
对于二阶,如上一个例子所使用的方程,我们需要把他拆分成两个一阶微分方程, y ′ = z , y ′ ′ = z ′ = − y y'= z, y'' = z'=-y y′=z,y′′=z′=−y,即:
{ d y d t = z d z d t = − y \left\{\begin{matrix} \frac{dy}{dt} &= z\\ \\ \frac{dz}{dt} &= -y\\ \end{matrix}\right. ⎩⎨⎧dtdydtdz=z=−y
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def fun(y_list, t):
y, z = y_list
dz = -y
dy = z
return dy, dz
t = np.arange(0, 5, 0.001)
y0 = [1, 1]
result = odeint(fun, y0, t)
plt.plot(t, result[:, 0])
plt.grid()
plt.show()
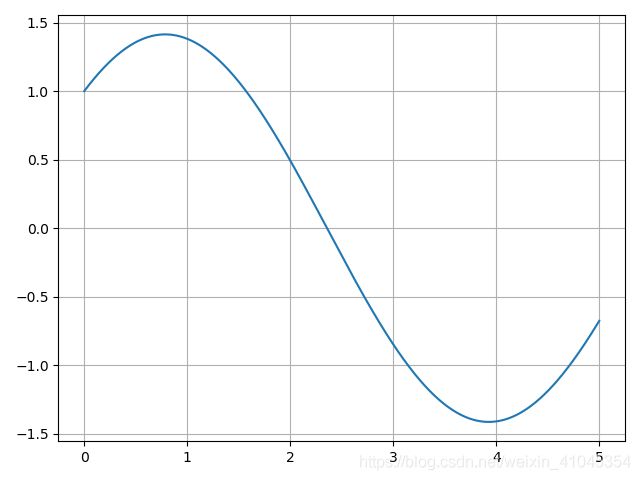
我们能得到相同的图案:
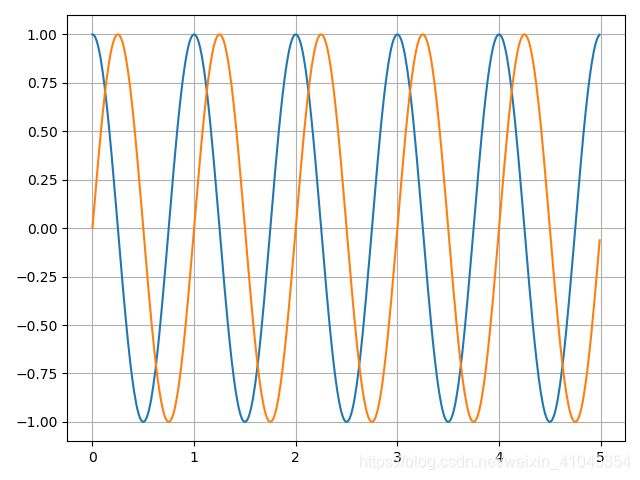
二、hopf振荡器实现
之前已经介绍过hopf振荡器的数学模型了,是一组微分方程
d x d t = α ( μ − r 2 ) x − ω y \frac{dx}{dt} = \alpha(\mu - r^2)x - \omega y dtdx=α(μ−r2)x−ωy
d y d t = α ( μ − r 2 ) y + ω x \frac {dy}{dt} = \alpha(\mu-r^2)y+\omega x dtdy=α(μ−r2)y+ωx下面我们用两种不同的方法去实现
1、numpy
这种方法比较传统,单纯地依靠numpy本身来进行运算,可以实现比较灵活改动。甚至能获取单个时间点的位置
def hopf(pos, steps, parms):
x, y = pos
alpha, a, mu, beta, omega = parms
r_square = x**2 + y**2
dx = alpha * (mu - r_square) * x - omega * y
dy = alpha * (mu - r_square) * y + omega * x
return [x+dx*steps, y+dy*steps]
我们只要通过以下方式调用就能获取到数据
d = []
for i in t:
p = hopf(p, time_steps, parms)
d.append(p)
2、odeint
这里跟第一章节差异不大,都是构造微分方程,然后计算数值解
def hopf(self, pos, time_steps):
x, y = pos
alpha, a, mu, beta, omega_sw = self.get_parms()
r_square = x**2 + y**2
# omega = np.pi
omega_st = ((1 - self.beta) / self.beta) * self.omega_sw
omega = omega_st / (np.e ** (-a * y) + 1) + omega_sw / (np.e ** (a * y) + 1)
dx = alpha * (mu - r_square) * x - omega * y
dy = alpha * (mu - r_square) * y + omega * x
return dx, dy
def calculate(self, t):
data = integrate.odeint(self.hopf, self.p0, t)
return data
t = np.arange(0, 5, self.time_steps)
date = self.calculate(t)
我们将其写成一个类,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
import time
# 0.027
class Cpg(object):
def __init__(self, alpha=100, a=50,
mu=1, beta=0.5, omega_sw=2*np.pi,
time_steps=0.01):
'''
初始化参数
'''
self.time_steps = time_steps
self.alpha = alpha
self.a = a
self.mu = mu
self.beta = beta
self.omega_sw = omega_sw
self.p0 = [1, 0]
def hopf(self, pos, time_steps):
'''
hopf振荡器数学模型
'''
x, y = pos
alpha, a, mu, beta, omega_sw = self.get_parms()
r_square = x**2 + y**2
# omega = np.pi
omega_st = ((1 - self.beta) / self.beta) * self.omega_sw
omega = omega_st / (np.e ** (-a * y) + 1) + omega_sw / (np.e ** (a * y) + 1)
dx = alpha * (mu - r_square) * x - omega * y
dy = alpha * (mu - r_square) * y + omega * x
return dx, dy
def get_parms(self):
'''
获取模型参数
'''
return self.alpha, self.a, self.mu, self.beta, self.omega_sw
def calculate(self, t):
'''
调用振荡器函数,返回数据序列
'''
data = integrate.odeint(self.hopf, self.p0, t)
return data
def show(self):
'''
将信号画出来
'''
t = np.arange(0, 5, self.time_steps)
t0 = time.time()
date = self.calculate(t)
t1 = time.time()
fig1 = plt.figure()
print('time: ', t1-t0)
plt.plot(t, date[:, 0])
plt.plot(t, date[:, 1])
plt.show()
fig2 = plt.figure()
plt.axis('equal')
plt.plot(date[:, 0], date[:, 1])
plt.show()
if __name__ == '__main__':
signal = Cpg()
signal.show()