二项式定理的初入

二项式定理

作者：Guo Linyi
这是本博客的第一篇笔记，具有纪念意义

---

二项式定理，又称牛顿二项式定理，由艾萨克·牛顿于1664-1665年提出
内容如下：
设n为一任意正整数，则对于任意的a和b，有如下性质：


在证明本定理之前，我们先暂时展开两个大家熟悉的特例：
1.（a+b）^2=a ^2+2ab+b ^2
2.（a+b）^3=a ^3+3a ^2 b+3ab ^2+b ^3
这时我们可以思考一下系数之间的关系
证明：
将（a+b） ^n展开直到没有括号为止
这时我们可以发现在展开过程中，每个因数都可以选择乘上x或y
所以每一项（总共n+1个项）都可以表达成x ^r*y ^(n-r)(0<=r<=n)//先抛开系数不说
利用C(n,m)+C(n,m-1)=C(n+1,m)做归纳证明
显然 x ^r*y ^(n-r) 的系数就是n的因子的m组合数即C(n,m)
得到了如上的结论：

---

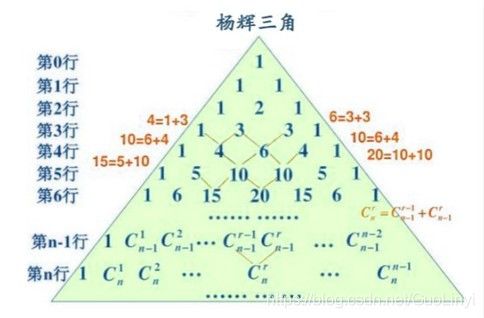
杨辉三角，又称帕斯卡三角形，是二项式系数在三角形中的一种几何排列。

我国南宋数学家杨辉所著的《详解九章算术》（1261年)一书中用如图的三角形解释二项和的乘方规律。

根据百度百科，杨辉三角其实就是古人对于两项高次幂各项系数的解释
它的构造:
边界为1，第n行第m列的值为第n-1行m-1列+第n-1行第m列
即递推关系式为f[n][m]=f[n-1][m-1]+f[n-1][m]

与杨辉三角联系最紧密的是二项式乘方展开式的系数规律，即二项式定理。

例如，在杨辉三角中，第3行的三个数恰好对应着两数和平方的展开式的每一项的系数
打个比方说，杨辉三角与二项式定理的邂逅是一对天然的数形趣遇或者数形结合

在信息学中，二项式定理是研究欧拉函数和莫比乌斯反演等数论函数
不过阶乘的倍增速度是很快的，所以我们不能直接通过二项式定理的结论进行求解
这个时候就需要用到杨辉三角这个**的东西
利用它与二项式定理的关系进行系数求解

例题

计算系数
给定一个多项式（by+ax）^ k,请求出x ^n * y ^m项的系数

输入格式
共一行，包含5个整数，分别为a,b,k,n,m,每两个整数之间用一个空格隔开
【数据范围】
对于30%的数据，有0<=k<=10
对于50%的数据，有a=1,b=1
对于100%的数据，有0<=k<=1000, 0<=n,m<=k且n+n=k,0<=a,b<=1,000,000

输出格式
共一行，包含一个整数，表示所求的系数，这个系数可能很大，输出对10007取模的结果

输入/输出例子
输入：
1 1 3 1 2
输出：
3

思路分析：
我们首先可以考虑通过二项式定理的通项公式进行通项求解
原式只是比（a+b）多了个原生系数（就是x,y）
所以对结果并没有什么影响
略去过程，得输出解应为 C(n,k)a ^n * b ^m
但是这个时候观察一下数据范围
k<=1000!!!
天哪，1000！的增长速度可是几何级别的，如果用for循环乘积求解
那么你会遭遇：
1.蒟佬的无情嘲讽
2.变量数据溢出
假如你还拿mod嘴硬，你回头自己看看数据量
随便几个数可以要了你的小命
所以，用二项式定理的结论无疑就是不明智的
我们可以考虑杨辉三角
通过它与二项式定理的关系间接求解
代码如下：

#include
using namespace std;
int k;
int n,m;
int a,b;
long long f[1010][1010];
long long ans=1;
int main()
{
    //std::ios::sync_with_stdio(false);
	scanf("%d%d",&a,&b);
	scanf("%d",&k);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=k+1;i++)
	{
		f[i][1]=1;
		f[i][i]=1;//边界初始化
	}
	for(int i=1;i<=k+1;i++)
	{
		for(int j=1;j<=i;j++)
		{
			if(j!=1&&j!=i) f[i][j]=f[i-1][j]+f[i-1][j-1],f[i][j]%=10007;//利用递推关系式
		}
	}
	for(int i=1;i<=n;i++) ans=(ans*a)%10007;
	for(int i=1;i<=m;i++) ans=(ans*b)%10007;
	printf("%lld",((f[k+1][k+1-m]%10007)*(ans%10007))%10007);//时刻要取模
	return 0;
}

若还想深入了解，请参考以下网址：
1.https://baike.so.com/doc/5391358-5628080.html 杨辉三角
2.https://oi-wiki.org/math/combination/ 排列组合
3.https://baike.so.com/doc/5409658-5647689.html 二项式定理
特别感谢：
https://oi-wiki.org/
http://47.112.229.113/
如有不足，还请各位大佬指出
END