TensorFlow 实战多元线性回归问题

作者：来自读者投稿

出品：Python数据之道

TensorFlow 实战

多元线性回归问题

本文小编将以一个具体例子来说明如何用 TensorFlow 来实现多元线性回归问题。我们以波士顿房价预测为例进行讲解。

1、 情景引入

波士顿房价数据集包括506个样本，每个样本包括12个特征变量和该地区的平均房价。房价显然和多个特征变量是相关的，因此需要选择多个特征变量来建立线性方程，这就是典型的多变量线性回归问题，下面是多元线性回归模型公式：

y=w0+w1x1+w2x2+...+wn*xn+b

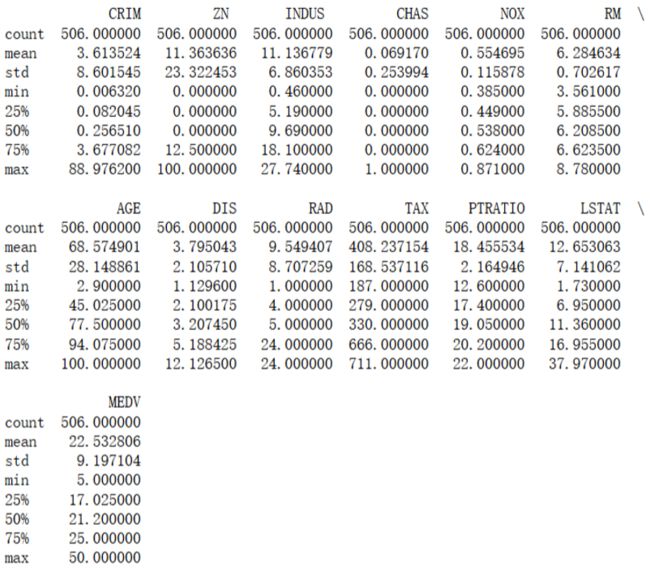
下面是波士顿房价的数据集部分展示，后面我们将使用数据集进行模型实现。

2、读取数据并归一化

通过pandas读取数据文件，列出统计概述。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import pandas as pd
#读取数据文件
df = pd.read_csv("./boston.csv",header=0)
#显示数据摘要描述信息
print(df.describe())

#对数据归一化到0-1之间
for i in range(12):
    df[:,i]=(df[:,i]-df[:,i].min())/(df[:,i].max()-df[:,i].min())
#x_data为归一化后的前12列特征数据
x_data = df[:,:12]
#y_data为最后一列标签数据
y_data = df[:12]

3、模型定义

首先定义特征数据和标签数据的占位符，shape中None表示行的数量未知，在实际训练时决定一次代入多少行样本，从一个样本的随机SDG到批量SDG都可以。

x = tf.placeholder(tf.float32,[None,12],name="x")
y = tf.placeholder(tf.float32,[None,1],name="y")

定义模型函数

4、训练模型

设置训练超参数

#迭代次数
train_epochs = 50
#学习率
learning_rate = 0.01

定义均方差损失函数

with tf.name_scope("LossFunction"):
    loss_function = tf.reduce_mean(tf.pow(y-pred,2)) #均方误差

选择优化器，初始化一个GradientDescentOptimizer

#梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

5、创建会话

声明会话

sess = tf.Session()

变量初始化

init = tf.global_variables_initializer()
sess.run(init)

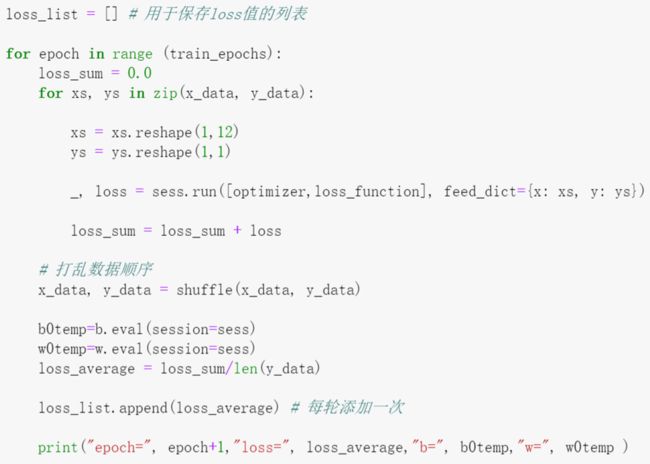
6、迭代训练

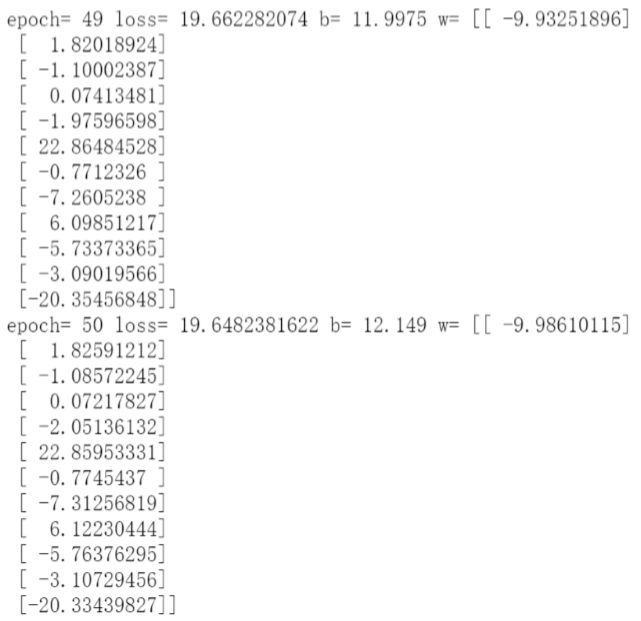
模型训练阶段，设置迭代次数，每次通过将样本逐个输入模型，进行梯度下降优化操作，每轮迭代后，绘制出模型曲线

下图为最后的训练结果

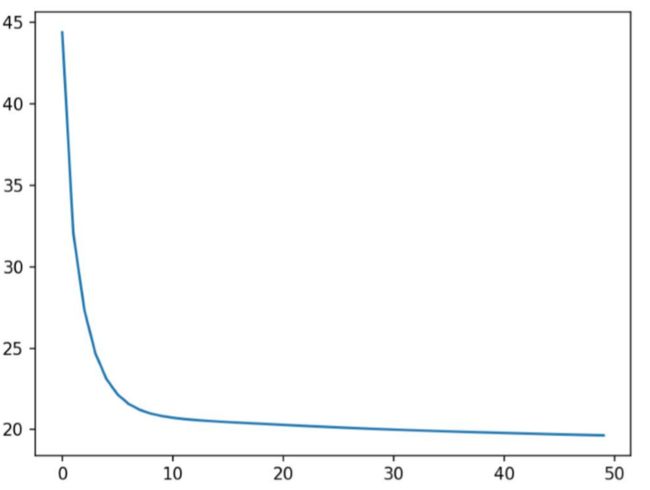
7、训练结果的可视化

plt.plot(loss_list)

8、TensorBoard 可视化

声明会话

sess = tf.Session()
#定义初始化变量的操作
init = tf.global_variables_initializer()

为 TensorBoard 可视化准备数据

#设置日志存储目录
logdir = 'd:/log'
sum_Loss = tf.summary.scalar("loss",loss_function)
merged = tf.summary.merge_all()

创建摘要的文件写入器

sess.run(init)
writer = tf.summary.FileWwriter(logdir,sess.graph)

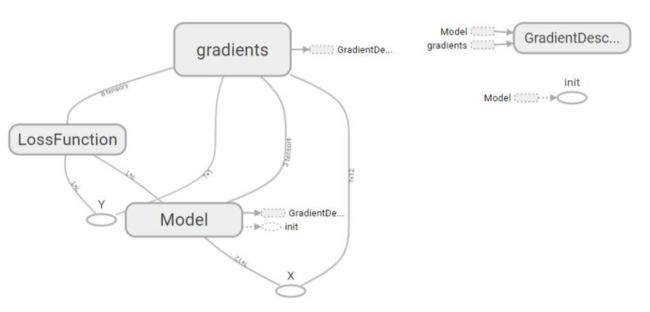
查看计算图

TensorBoard查看loss

好啦，最后赶快动手尝试一下属于你们的第一个多元回归模型的建立吧！

本文来自读者投稿，欢迎大家点击下面链接进行投稿：

欢迎投稿

---------End---------

关注后回复“w”，加我私人微信

“分享”和“在看”是更好的支持！