SIFT算法之python实现
0. 算法原理细节可参考:
- https://blog.csdn.net/abcjennifer/article/details/7639681
- https://blog.csdn.net/zddblog/article/details/7521424?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1
- https://www.bilibili.com/video/BV1Qb411W7cK?p=1
本文参考了up主的代码,并在匹配阶段、金字塔输出方式等部分进行了重新设计,同时使代码实现完全对像素操作。
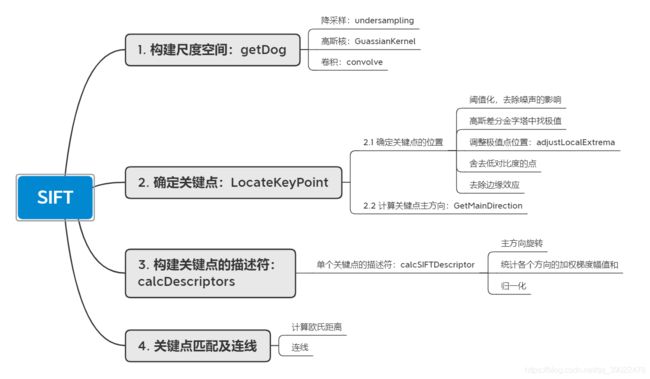
1. 算法流程
SIFT(Scale-invariant feature transform),即尺度不变特征变换,是一种检测图像局部特征并进行特征点匹配的算法。
2. python实现
OPENCV库中有SIFT函数,调用此函数很容易实现。下面的是直接对像素操作实现SIFT的源代码。
# coding: utf-8
import warnings
warnings.filterwarnings("ignore") # 忽略警告
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
def convolve(kernel, img, padding, strides):
'''
:param kernel: 输入的核函数
:param img: 输入的图片
:param padding: 需要填充的位置
:param strides: 高斯核移动的步长
:return: 返回卷积的结果
'''
result = None
kernel_size = kernel.shape
img_size = img.shape
if len(img_size) == 3: # 三通道图片就对每通道分别卷积 dstack和并
channel = []
for i in range(img_size[-1]):
pad_img = np.pad(img[:, :, i], ((padding[0], padding[1]), (padding[2], padding[3])), 'constant')
temp = []
for j in range(0, img_size[0], strides[1]):
temp.append([])
for k in range(0, img_size[1], strides[0]):
val = (kernel * pad_img[j * strides[1]:j * strides[1] + kernel_size[0],
k * strides[0]:k * strides[0] + kernel_size[1]]).sum()
temp[-1].append(val)
channel.append(np.array(temp))
channel = tuple(channel)
result = np.dstack(channel)
elif len(img_size) == 2:
channel = []
pad_img = np.pad(img, ((padding[0], padding[1]), (padding[2], padding[3])),
'constant') # pad是填充函数 边界处卷积需要对边界外根据高斯核大小填0
for j in range(0, img_size[0], strides[1]): # 第j列 strides 是步长 本例步长为1 相当于遍历
channel.append([])
for k in range(0, img_size[1], strides[0]): # 第i行
val = (kernel * pad_img[j * strides[1]:j * strides[1] + kernel_size[0],
k * strides[0]:k * strides[0] + kernel_size[1]]).sum() # 卷积的定义 相当于用高斯核做加权和
channel[-1].append(val)
result = np.array(channel)
return result
# 函数1.1.1 undersampling
# 降采样,隔点取点
def undersampling(img, step=2):
'''
临近降采样
:param img: 输入图片
:param step: 降采样步长 默认为2(缩小两倍)
:return: 返回降采样结果
'''
return img[::step, ::step]
# 函数1.1.2 GuassianKernel
# 产生高斯核
def GuassianKernel(sigma, dim):
'''
:param sigma: 标准差
:param dim: 高斯核的纬度(必须是个奇数)
:return: 返回高斯核
'''
temp = [t - (dim // 2) for t in range(dim)] # 生成二维高斯的x与y
assistant = []
for i in range(dim):
assistant.append(temp)
assistant = np.array(assistant)
temp = 2 * sigma * sigma
result = (1.0 / (temp * np.pi)) * np.exp(-(assistant ** 2 + (assistant.T) ** 2) / temp) # 二维高斯公式
return result
# 函数1.1,getDoG
# 得到高斯金字塔和高斯差分金字塔
def getDoG(img, n, sigma0, S=None, O=None):
'''
:param img: 输入的图像
:param sigma0: 输入的sigma
:param n: 有几层用于提取特征
:param S: 金字塔每层有几张gauss滤波后的图像
:param O: 金字塔有几层
:return: 返回差分高斯金字塔和高斯金字塔
'''
if S == None:
S = n + 3 # 至少有4张 (第一张和最后一张高斯金字塔无法提取特征,差分以后的第一张和最后一张也无法提取特征)
if O == None:
O = int(np.log2(min(img.shape[0], img.shape[1]))) - 3 # 计算最大可以计算多少层 O=log2(min(img长,img宽))-3
k = 2 ** (1.0 / n)
sigma = [[(k ** s) * sigma0 * (1 << o) for s in range(S)] for o in range(O)] # 每一层 sigma按照 k^1/s * sigama0 排列 下一层的sigma都要比上一层sigma大两倍
sample = [undersampling(img, 1 << o) for o in range(O)] # 降采样取图片作为该层的输入
Guass_Pyramid = []
for i in range(O):
Guass_Pyramid.append([]) # 申明二维空数组
for j in range(S):
dim = int(6*sigma[i][j] + 1) # 上网查找相关信息 高斯核大小随sigma变化的效果更好
#dim = int(9)
if dim % 2 == 0: # 防止输入的高斯核不是奇数
dim += 1
Guass_Pyramid[-1].append(convolve(GuassianKernel(sigma[i][j], dim), sample[i], [dim // 2, dim // 2, dim // 2, dim // 2], [1, 1])) # 在第i层添加第j张 经过高斯卷积的 该图片四周扩展 5//2=2 用于高斯卷积
DoG_Pyramid = [[Guass_Pyramid[o][s + 1] - Guass_Pyramid[o][s] for s in range(S - 1)] for o in range(O)] #每一层中 上一张减去下一张得到高斯核
return DoG_Pyramid, Guass_Pyramid, O # 返回高斯金字塔和高斯差分金字塔
# 函数2.1.1 adjustLocalExtrema
# 功能:通过泰勒展开精调位置精调位置
def adjustLocalExtrema(DoG, o, s, x, y, contrastThreshold, edgeThreshold, sigma, n, SIFT_FIXPT_SCALE):
SIFT_MAX_INTERP_STEPS = 5
SIFT_IMG_BORDER = 5
point = []
img_scale = 1.0 / (255 * SIFT_FIXPT_SCALE)
deriv_scale = img_scale * 0.5
second_deriv_scale = img_scale
cross_deriv_scale = img_scale * 0.25
img = DoG[o][s]
i = 0
while i < SIFT_MAX_INTERP_STEPS:
if s < 1 or s > n or y < SIFT_IMG_BORDER or y >= img.shape[1] - SIFT_IMG_BORDER or x < SIFT_IMG_BORDER or x >= \
img.shape[0] - SIFT_IMG_BORDER:
return None, None, None, None
img = DoG[o][s]
prev = DoG[o][s - 1]
next = DoG[o][s + 1]
dD = [(img[x, y + 1] - img[x, y - 1]) * deriv_scale,
(img[x + 1, y] - img[x - 1, y]) * deriv_scale,
(next[x, y] - prev[x, y]) * deriv_scale]
v2 = img[x, y] * 2
dxx = (img[x, y + 1] + img[x, y - 1] - v2) * second_deriv_scale
dyy = (img[x + 1, y] + img[x - 1, y] - v2) * second_deriv_scale
dss = (next[x, y] + prev[x, y] - v2) * second_deriv_scale
dxy = (img[x + 1, y + 1] - img[x + 1, y - 1] - img[x - 1, y + 1] + img[x - 1, y - 1]) * cross_deriv_scale
dxs = (next[x, y + 1] - next[x, y - 1] - prev[x, y + 1] + prev[x, y - 1]) * cross_deriv_scale
dys = (next[x + 1, y] - next[x - 1, y] - prev[x + 1, y] + prev[x - 1, y]) * cross_deriv_scale
H = [[dxx, dxy, dxs],
[dxy, dyy, dys],
[dxs, dys, dss]]
X = np.matmul(np.linalg.pinv(np.array(H)), np.array(dD))
xi = -X[2]
xr = -X[1]
xc = -X[0]
if np.abs(xi) < 0.5 and np.abs(xr) < 0.5 and np.abs(xc) < 0.5:
break
y += int(np.round(xc))
x += int(np.round(xr))
s += int(np.round(xi))
i += 1
if i >= SIFT_MAX_INTERP_STEPS:
return None, x, y, s
if s < 1 or s > n or y < SIFT_IMG_BORDER or y >= img.shape[1] - SIFT_IMG_BORDER or x < SIFT_IMG_BORDER or x >= \
img.shape[0] - SIFT_IMG_BORDER:
return None, None, None, None
t = (np.array(dD)).dot(np.array([xc, xr, xi]))
contr = img[x, y] * img_scale + t * 0.5
# 确定极值点位置第四步:舍去低对比度的点
if np.abs(contr) * n < contrastThreshold:
return None, x, y, s
# 确定极值点位置第五步:边缘效应的去除。 利用Hessian矩阵的迹和行列式计算主曲率的比值
tr = dxx + dyy
det = dxx * dyy - dxy * dxy
if det <= 0 or tr * tr * edgeThreshold >= (edgeThreshold + 1) * (edgeThreshold + 1) * det:
return None, x, y, s
point.append((x + xr) * (1 << o))
point.append((y + xc) * (1 << o))
point.append(o + (s << 8) + (int(np.round((xi + 0.5)) * 255) << 16))
point.append(sigma * np.power(2.0, (s + xi) / n) * (1 << o) * 2)
return point, x, y, s
def GetMainDirection(img, r, c, radius, sigma, BinNum):
expf_scale = -1.0 / (2.0 * sigma * sigma)
X = []
Y = []
W = []
temphist = []
for i in range(BinNum):
temphist.append(0.0)
# 图像梯度直方图统计的像素范围
k = 0
for i in range(-radius, radius + 1):
y = r + i
if y <= 0 or y >= img.shape[0] - 1:
continue
for j in range(-radius, radius + 1):
x = c + j
if x <= 0 or x >= img.shape[1] - 1:
continue
dx = (img[y, x + 1] - img[y, x - 1])
dy = (img[y - 1, x] - img[y + 1, x])
X.append(dx)
Y.append(dy)
W.append((i * i + j * j) * expf_scale)
k += 1
length = k
W = np.exp(np.array(W))
Y = np.array(Y)
X = np.array(X)
Ori = np.arctan2(Y, X) * 180 / np.pi
Mag = (X ** 2 + Y ** 2) ** 0.5
# 计算直方图的每个bin
for k in range(length):
bin = int(np.round((BinNum / 360.0) * Ori[k]))
if bin >= BinNum:
bin -= BinNum
if bin < 0:
bin += BinNum
temphist[bin] += W[k] * Mag[k]
# smooth the histogram
# 高斯平滑
temp = [temphist[BinNum - 1], temphist[BinNum - 2], temphist[0], temphist[1]]
temphist.insert(0, temp[0])
temphist.insert(0, temp[1])
temphist.insert(len(temphist), temp[2])
temphist.insert(len(temphist), temp[3]) # padding
hist = []
for i in range(BinNum):
hist.append(
(temphist[i] + temphist[i + 4]) * (1.0 / 16.0) + (temphist[i + 1] + temphist[i + 3]) * (4.0 / 16.0) +
temphist[i + 2] * (6.0 / 16.0))
# 得到主方向
maxval = max(hist)
return maxval, hist
# 函数2.1 LocateKeyPoint
# 功能:关键点定位,共分为5步
def LocateKeyPoint(DoG, sigma, GuassianPyramid, n, BinNum=36, contrastThreshold=0.04, edgeThreshold=10.0):
SIFT_ORI_SIG_FCTR = 1.52
SIFT_ORI_RADIUS = 3 * SIFT_ORI_SIG_FCTR
SIFT_ORI_PEAK_RATIO = 0.8
SIFT_INT_DESCR_FCTR = 512.0
# SIFT_FIXPT_SCALE = 48
SIFT_FIXPT_SCALE = 1
KeyPoints = []
O = len(DoG)
S = len(DoG[0])
for o in range(O):
for s in range(1, S - 1):
# 第一步:设定阈值
threshold = 0.5 * contrastThreshold / (n * 255 * SIFT_FIXPT_SCALE)# 用于阈值化,去噪
img_prev = DoG[o][s - 1]
img = DoG[o][s]
img_next = DoG[o][s + 1]
for i in range(img.shape[0]):
for j in range(img.shape[1]):
val = img[i, j]
eight_neiborhood_prev = img_prev[max(0, i - 1):min(i + 2, img_prev.shape[0]), max(0, j - 1):min(j + 2, img_prev.shape[1])]
eight_neiborhood = img[max(0, i - 1):min(i + 2, img.shape[0]), max(0, j - 1):min(j + 2, img.shape[1])]
eight_neiborhood_next = img_next[max(0, i - 1):min(i + 2, img_next.shape[0]), max(0, j - 1):min(j + 2, img_next.shape[1])]
# 第二步:阈值化,在高斯差分金字塔中找极值
if np.abs(val) > threshold and \
((val > 0 and (val >= eight_neiborhood_prev).all() and (val >= eight_neiborhood).all() and (
val >= eight_neiborhood_next).all())
or (val < 0 and (val <= eight_neiborhood_prev).all() and (
val <= eight_neiborhood).all() and (val <= eight_neiborhood_next).all())): # 如果某点大于阈值,并且 比周围8个点、上下2*9个点共26个点都大或都小,则认为是关键点
# 第三步:精调位置,通过函数2.1.1 adjustLocalExtrema:实现
point, x, y, layer = adjustLocalExtrema(DoG, o, s, i, j, contrastThreshold, edgeThreshold,
sigma, n, SIFT_FIXPT_SCALE)
if point == None:
continue
scl_octv = point[-1] * 0.5 / (1 << o)
# GetMainDirection:(确定极值点的位置以后就)求主方向
omax, hist = GetMainDirection(GuassianPyramid[o][layer], x, y,
int(np.round(SIFT_ORI_RADIUS * scl_octv)),
SIFT_ORI_SIG_FCTR * scl_octv, BinNum)
mag_thr = omax * SIFT_ORI_PEAK_RATIO
for k in range(BinNum):
if k > 0:
l = k - 1
else:
l = BinNum - 1
if k < BinNum - 1:
r2 = k + 1
else:
r2 = 0
if hist[k] > hist[l] and hist[k] > hist[r2] and hist[k] >= mag_thr:
bin = k + 0.5 * (hist[l] - hist[r2]) / (hist[l] - 2 * hist[k] + hist[r2])
if bin < 0:
bin = BinNum + bin
else:
if bin >= BinNum:
bin = bin - BinNum
temp = point[:]
temp.append((360.0 / BinNum) * bin)
KeyPoints.append(temp)
return KeyPoints
# calcSIFTDescriptor:更小的计算描述符函数
def calcSIFTDescriptor(img, ptf, ori, scl, d, n, SIFT_DESCR_SCL_FCTR=3.0, SIFT_DESCR_MAG_THR=0.2,
SIFT_INT_DESCR_FCTR=512.0, FLT_EPSILON=1.19209290E-07):
dst = []
pt = [int(np.round(ptf[0])), int(np.round(ptf[1]))] # 坐标点取整
# 旋转到主方向
cos_t = np.cos(ori * (np.pi / 180)) # 余弦值
sin_t = np.sin(ori * (np.pi / 180)) # 正弦值
bins_per_rad = n / 360.0
exp_scale = -1.0 / (d * d * 0.5)
hist_width = SIFT_DESCR_SCL_FCTR * scl
# radius: 统计区域边长的一半
radius = int(np.round(hist_width * 1.4142135623730951 * (d + 1) * 0.5))
cos_t /= hist_width
sin_t /= hist_width
rows = img.shape[0]
cols = img.shape[1]
hist = [0.0] * ((d + 2) * (d + 2) * (n + 2))
X = []
Y = []
RBin = []
CBin = []
W = []
k = 0
for i in range(-radius, radius + 1):
for j in range(-radius, radius + 1):
c_rot = j * cos_t - i * sin_t
r_rot = j * sin_t + i * cos_t
rbin = r_rot + d // 2 - 0.5
cbin = c_rot + d // 2 - 0.5
r = pt[1] + i
c = pt[0] + j
if rbin > -1 and rbin < d and cbin > -1 and cbin < d and r > 0 and r < rows - 1 and c > 0 and c < cols - 1:
dx = (img[r, c + 1] - img[r, c - 1])
dy = (img[r - 1, c] - img[r + 1, c])
X.append(dx)
Y.append(dy)
RBin.append(rbin)
CBin.append(cbin)
W.append((c_rot * c_rot + r_rot * r_rot) * exp_scale)
k += 1
length = k
Y = np.array(Y)
X = np.array(X)
Ori = np.arctan2(Y, X) * 180 / np.pi
Mag = (X ** 2 + Y ** 2) ** 0.5
W = np.exp(np.array(W))
for k in range(length):
rbin = RBin[k]
cbin = CBin[k]
obin = (Ori[k] - ori) * bins_per_rad
mag = Mag[k] * W[k]
r0 = int(rbin)
c0 = int(cbin)
o0 = int(obin)
rbin -= r0
cbin -= c0
obin -= o0
if o0 < 0:
o0 += n
if o0 >= n:
o0 -= n
# histogram update using tri-linear interpolation
v_r1 = mag * rbin
v_r0 = mag - v_r1
v_rc11 = v_r1 * cbin
v_rc10 = v_r1 - v_rc11
v_rc01 = v_r0 * cbin
v_rc00 = v_r0 - v_rc01
v_rco111 = v_rc11 * obin
v_rco110 = v_rc11 - v_rco111
v_rco101 = v_rc10 * obin
v_rco100 = v_rc10 - v_rco101
v_rco011 = v_rc01 * obin
v_rco010 = v_rc01 - v_rco011
v_rco001 = v_rc00 * obin
v_rco000 = v_rc00 - v_rco001
idx = ((r0 + 1) * (d + 2) + c0 + 1) * (n + 2) + o0
hist[idx] += v_rco000
hist[idx + 1] += v_rco001
hist[idx + (n + 2)] += v_rco010
hist[idx + (n + 3)] += v_rco011
hist[idx + (d + 2) * (n + 2)] += v_rco100
hist[idx + (d + 2) * (n + 2) + 1] += v_rco101
hist[idx + (d + 3) * (n + 2)] += v_rco110
hist[idx + (d + 3) * (n + 2) + 1] += v_rco111
# finalize histogram, since the orientation histograms are circular
for i in range(d):
for j in range(d):
idx = ((i + 1) * (d + 2) + (j + 1)) * (n + 2)
hist[idx] += hist[idx + n]
hist[idx + 1] += hist[idx + n + 1]
for k in range(n):
dst.append(hist[idx + k])
# copy histogram to the descriptor,
# apply hysteresis thresholding
# and scale the result, so that it can be easily converted
# to byte array
nrm2 = 0
length = d * d * n
for k in range(length):
nrm2 += dst[k] * dst[k]
thr = np.sqrt(nrm2) * SIFT_DESCR_MAG_THR
nrm2 = 0
for i in range(length):
val = min(dst[i], thr)
dst[i] = val
nrm2 += val * val
nrm2 = SIFT_INT_DESCR_FCTR / max(np.sqrt(nrm2), FLT_EPSILON) # 归一化
for k in range(length):
dst[k] = min(max(dst[k] * nrm2, 0), 255)
return dst
# calcDescriptors:计算描述符
def calcDescriptors(gpyr, keypoints, SIFT_DESCR_WIDTH=4, SIFT_DESCR_HIST_BINS=8):
# SIFT_DESCR_WIDTH = 4,描述直方图的宽度
# SIFT_DESCR_HIST_BINS = 8
d = SIFT_DESCR_WIDTH
n = SIFT_DESCR_HIST_BINS
descriptors = []
# keypoints(x,y,低8位组数次8位层数,尺度,主方向)
for i in range(len(keypoints)):
kpt = keypoints[i]
o = kpt[2] & 255 # 组序号
s = (kpt[2] >> 8) & 255 # 该特征点所在的层序号
scale = 1.0 / (1 << o) # 缩放倍数
size = kpt[3] * scale # 该特征点所在组的图像尺寸
ptf = [kpt[1] * scale, kpt[0] * scale] # 该特征点在金字塔组中的坐标
img = gpyr[o][s] # 该点所在的金字塔图像
descriptors.append(calcSIFTDescriptor(img, ptf, kpt[-1], size * 0.5, d, n)) # calcSIFTDescriptor:更小的计算描述符函数
return descriptors
def SIFT(img, showDoGimgs=False):
# 1. 建立高斯差分金字塔,
SIFT_SIGMA = 1.6
SIFT_INIT_SIGMA = 0.5 # 假设的摄像头的尺度
sigma0 = np.sqrt(SIFT_SIGMA ** 2 - SIFT_INIT_SIGMA ** 2) #初始sigma0
n = 2######
DoG, GuassianPyramid,octaves = getDoG(img, n, sigma0) # 函数1.1,getDoG:得到高斯金字塔和高斯差分金字塔
if showDoGimgs:
plt.figure(1)
for i in range(octaves):
for j in range(n + 3):
array = np.array(GuassianPyramid[i][j], dtype=np.float32)
plt.subplot(octaves, n + 3, j + (i) * octaves + 1)
plt.imshow(array.astype(np.uint8), cmap='gray')
plt.axis('off')
plt.show()
plt.figure(2)
for i in range(octaves):
for j in range(n + 2):
array = np.array(DoG[i][j], dtype=np.float32)
plt.subplot(octaves, n + 3, j + (i) * octaves + 1)
plt.imshow(array.astype(np.uint8), cmap='gray')
plt.axis('off')
plt.show()
#2. 确定关键点位置,为关键点赋予方向
KeyPoints = LocateKeyPoint(DoG, SIFT_SIGMA, GuassianPyramid, n) # 函数2.1,LocateKeyPoint:关键点定位
#3. 计算关键点的描述符
discriptors = calcDescriptors(GuassianPyramid, KeyPoints) # 函数3.1,calcDescriptors:计算描述符
return KeyPoints, discriptors
def Lines(img, info, color=(255, 0, 0), err=700):
if len(img.shape) == 2:
result = np.dstack((img, img, img))
else:
result = img
k = 0
for i in range(result.shape[0]):
for j in range(result.shape[1]):
temp = (info[:, 1] - info[:, 0])
A = (j - info[:, 0]) * (info[:, 3] - info[:, 2])
B = (i - info[:, 2]) * (info[:, 1] - info[:, 0])
temp[temp == 0] = 1e-9
t = (j - info[:, 0]) / temp
e = np.abs(A - B)
temp = e < err
if (temp * (t >= 0) * (t <= 1)).any():
result[i, j] = color
k += 1
#print(k)
return result
def drawLines(X1, X2, Y1, Y2, dis, img, num=10):
info = list(np.dstack((X1, X2, Y1, Y2, dis))[0])
info = sorted(info, key=lambda x: x[-1])
info = np.array(info)
info = info[:min(num, info.shape[0]), :]
img = Lines(img, info)
# plt.imsave('./sift/3.jpg', img)
if len(img.shape) == 2:
plt.imshow(img.astype(np.uint8), cmap='gray')
else:
plt.imshow(img.astype(np.uint8))
plt.axis('off')
# plt.plot([info[:,0], info[:,1]], [info[:,2], info[:,3]], 'c')
# fig = plt.gcf()
# fig.set_size_inches(int(img.shape[0]/100.0),int(img.shape[1]/100.0))
plt.savefig('result.jpg')
plt.show()
if __name__ == '__main__':
origimg = plt.imread(r'01.jpg') # 读第一张图片
if len(origimg.shape) == 3:#如果是彩色图,就按照三通道取均值的方式转成灰度图
img = origimg.mean(axis=-1)
else:
img = origimg
keyPoints, discriptors = SIFT(img) # 用SIFT算法计算关键点(x坐标,y坐标,sigma,主方向,梯度幅值)和描述符(128维的向量)
origimg2 = plt.imread(r'02.jpg') # 读第二张图片
if len(origimg.shape) == 3:
img2 = origimg2.mean(axis=-1)
else:
img2 = origimg2
ScaleRatio = img.shape[0] * 1.0 / img2.shape[0]
img2 = np.array(Image.fromarray(img2).resize((int(round(ScaleRatio * img2.shape[1])), img.shape[0]), Image.BICUBIC))
keyPoints2, discriptors2 = SIFT(img2) # 用SIFT算关键点和描述符
indexs = []
deltas = []
for i in range(len(keyPoints2)):
ds = discriptors2[i]
mindetal = 10000000
index = -1
detal = 0
for j in range(len(keyPoints)):
ds0 = discriptors[j]
d = np.array(ds)-np.array(ds0)
detal = d.dot(d)
if( detal <= mindetal):
mindetal = detal
index = j
indexs.append(index)
deltas.append(mindetal)
keyPoints = np.array(keyPoints)[:,:2]
keyPoints2 = np.array(keyPoints2)[:,:2]
keyPoints2[:, 1] = img.shape[1] + keyPoints2[:, 1]
origimg2 = np.array(Image.fromarray(origimg2).resize((img2.shape[1],img2.shape[0]), Image.BICUBIC))
result = np.hstack((origimg,origimg2))
keyPoints = keyPoints[indexs[:]]
X1 = keyPoints[:, 1]
X2 = keyPoints2[:, 1]
Y1 = keyPoints[:, 0]
Y2 = keyPoints2[:, 0]
drawLines(X1,X2,Y1,Y2,deltas,result)#把匹配的结果放到这里画线
3. 算法结果
最终展示ppt:
链接:https://pan.baidu.com/s/1Y1Os2imDhRvNptHwWShdBw
提取码:2n0s