全景拼接图像的实现

全景拼接图像

全景拼接图像是指在同一位置（即图像的照相机位置相同）拍摄的两幅或者多幅图像用某种方式拼接起来。
基本步骤如下：
实验步骤：
步骤一：输入图像;
步骤二：应用SIFT算法对图像进行特征提取, 提取图像的特征点, 粗匹配特征点;
步骤三：用RANSAC方法对变换矩阵进行求解与精炼，并去除匹配错误点;
步骤四：根据最后计算出的变化矩阵进行图像拼接。

1.RANSAC算法原理

在用SIFT算法找到了匹配点，但这里面还存在着错误的匹配对，我们采用RANSAC算法对这些错误的匹配对再次进行剔除，从而得到有较高正确度的匹配对。RANSAC算法是依据一个容许误差将所有的粗匹配特征点分成内、外点，再利用内点的数据与准确的特点进行参数估计比较，从而剔除错误特征点。
采用RANSAC算法剔除误匹配点对，需要计算出待匹配图像之间的坐标转换关系。根据找到的匹配特点对，可计算出图像间的坐标转换关系，即两幅图像之间的变换矩阵。设图像间的变换为投影变换，那么

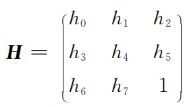
若ｐ＝（x,y），ｑ＝（x’,y’）是 匹 配 的 特 征 点 对，则投影变换公式为:

由投影变换公式可计算出Ｈ的各自由度参数(i=0,…,7)，并以此作为初始值，通过迭代精炼Ｈ，可进一步确定特征点的对应，直到对应点数目不变为止，从而完成图像配准。
RANSAC算法的思想是：首先随机地选择两个点，这两个点确定了一条直线，并且称在这条直线的一定范围内的点为这条直线的支撑。这样的随机选择重复数次，然后，具有最大支撑集的直线被确认为是样本点集的拟合。在拟合的误差距离范围内的点被认为是内点，它们构成一致集，反之则为外点。
RANSAC算法剔除错误匹配对实现:
步骤一：设定初始最佳内点数为 0。从N对预匹配特征点中随机选取 4 对点建立方程组，求解出变换矩阵H的4组特征点的值。
步骤二：计算其余N对特征点经过变化矩阵H 的坐标值与预匹配点之间的距离 dv 。
步骤三：若 dv 小于设定的阈值T，则定这个预匹配为内点，反之为外点。
步骤四：统计当前的内点数目，若数目大于预设的最低匹配点个数，则记录当前变换矩阵H
步骤五：另选 4 对预匹配点，重复步骤一 ～ 四 若干次后，选择内点最多的变换矩阵作为参考变换矩阵，此时的变换矩阵为最佳结果。

2.实验过程详解

2.1 稳健的单应性矩阵估计
在使用RANSAC算法得出最佳变换矩阵之前，我们需要先使用SIFT特征自动找到匹配对应，在这个基础上删去错误的匹配点，得到最佳的变换矩阵。

import sift
#设置图像位置
featname = ['C:/Users/LENOVO/Desktop/计算机视觉/pcv-book-code-master/ch03/images/'+str(i+1)+'.sift' for i in range(5)] 
imname = ['C:/Users/LENOVO/Desktop/计算机视觉/pcv-book-code-master/ch03/images/'+str(i+1)+'.jpg' for i in range(5)]

#提取特征点并提取
l = {}
d = {}
for i in range(5): 
    sift.process_image(imname[i],featname[i])
    l[i],d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i+1],d[i])

# 可视化匹配 
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i+1]))
    figure()
    sift.plot_matches(im2,im1,l[i+1],l[i],matches[i],show_below=True)

接下来使用RANSAC算法来求解单应性矩阵，分三步走。
1）将下面的模型类添加到homography.py文件中

class RansacModel(object):
    """ 用于测试单应性矩阵的类，其中单应性矩阵是由网站
        http://www.scipy.org/Cookbook/RANSAC上的ransac.py计算出来的"""
    
    def __init__(self,debug=False):
        self.debug = debug
        
    def fit(self, data):
        """ 计算选取的4个对应的单应性矩阵 """
        
        # 将其转置，来调用H_from_points（）计算单应性矩阵
        data = data.T
        
        # 映射的起始点
        fp = data[:3,:4]
        # 映射的目标点
        tp = data[3:,:4]
        
        #计算单应性矩阵，然后返回
        return H_from_points(fp,tp)
    
    def get_error( self, data, H):
        """ 对所有对应计算单应性矩阵，然后对每个变换后的点，返回相应的误差"""
        
        data = data.T
        
        # 映射的起始点
        fp = data[:3]
        # 映射的目标点
        tp = data[3:]
        
        # 变换fp
        fp_transformed = dot(H,fp)
        
        # 归一化齐次坐标
        fp_transformed = normalize(fp_transformed)
                
        # 返回每个点的误差
        return sqrt( sum((tp-fp_transformed)**2,axis=0) )

在这模型类中，要注意仅仅接受由ransac.py选择的4个对应点对，然后你和一个单应性矩阵。get_error（）方法对美个对应点对使用该单应性矩阵，然后返回相应的平方距离值和，因此RANSAC算法能够判定哪些点是对的哪些是错误的。
2）在实际的实验中，我们需要在距离上使用一个阈值来决定哪些单应性矩阵是合理的

def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):
    """ 使用RANSAC稳健性估计点对应的单应性矩阵H(ransac.py 来自
        http://www.scipy.org/Cookbook/RANSAC).
        
        输入:齐次坐标表示的点 fp,tp (3*n arrays)  """
    
    from PCV.tools import ransac
    
    # 对应点组
    data = vstack((fp,tp))
    
    #计算H，并返回
    H,ransac_data = ransac.ransac(data.T,model,4,maxiter,match_theshold,10,return_all=True)
    return H,ransac_data['inliers']

该函数的返回结果为单应性矩阵和对应该单应矩阵的正确点对数。
最后我们返回我们的主函数。将RANSAC算法应用与对应点对上：

# 将匹配点转换为齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j+1][ndx,:2].T) 
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2,:2].T) 
    
    # 切换x和y -TODO应该会移动到其他地方
    fp = vstack([fp[1],fp[0],fp[2]])
    tp = vstack([tp[1],tp[0],tp[2]])
    return fp,tp


# 估计单应性矩阵
model = homography.RansacModel() 

fp,tp = convert_points(1)
H_12 = homography.H_from_ransac(fp,tp,model)[0] #im 1 to 2 

fp,tp = convert_points(0)
H_01 = homography.H_from_ransac(fp,tp,model)[0] #im 0 to 1 

tp,fp = convert_points(2) #注意: 点是反序的
H_32 = homography.H_from_ransac(fp,tp,model)[0] #im 3 to 2 

tp,fp = convert_points(3)  #注意: 点是反序的
H_43 = homography.H_from_ransac(fp,tp,model)[0] #im 4 to 3    

2.2 图像拼接
本实验中的图像拼接方法：是将所有的图像扭曲到一个公共的图像平面上。通常，这里的公共平面为中心图像平面。创建一个很大的图像，比如图像中全部填充0，时其和中心图像平信，然后将所有的图像扭曲到上面。在本次实验中我们将中心图像左边或者右边的区域填充为0，以便为扭曲的图像腾出空间。

3. 实验结果分析

室内场景拼接
原图：

拼接结果：

从这张实验结果图可得知右边的拼接的效果一般，仔细分析下：是因为中间黑红色海报的那张图的最左边拍到了一部分右边蓝色海报的部分（特征信息比较少），但这部分与其右边的第一张图片的蓝色海报相匹配，但因为特征信息比较少，导致此处拼接效果差。然后，最右边的图片与倒数第二张图片的效果差是因为选取的特征点有问题。它们两张图的特征点可能大部分都在海报背后的栏杆上，特征点匹配也存在问题，导致拼接效果差。

景深落差小的室外场景拼接
景深落差小是指都拍远景，然后景深落差大是指你在拍远景的时候突然有个是近景的物体拍进去了，然后但是也能很好的拼接起来。
在此次实验过程中，匹配失败的情况经常发生，下面我给大家看下失败的情况：
原图1：

实验结果图1：

在这个实验结果图可知，这三张不连贯的拼接图，左第一张图是第4、5张原图拼接而成，中间的图仅仅是第1张图的扭曲，右边的图是原图第2、3张图拼接而成，可能出现的这种情况的原因：第一张图与第二张图没有拼接起来，可能因为能经过筛选的特征点匹配对数少（可能是草坪占的比例过大，且其没有明显特征）。第3张图与第4张图没有拼接起来，可能原因如上。总结：使用此算法时，对拍摄的图片要求比较高，需要找到更好的算法优化他。
实验结果正确的分析：
基于上述的失败原因，本次拍摄的图片，规避了大比例相似的场景。
原图2：

实验结果图2：

这张实验结果图比上一张的效果好很多，可能的原因是这张图的匹配的特征点比较正确，拼接的缝隙从远处看基本看不出来，但其实这张图从根本上我的肉眼观察中：只用了两张图片，最左边和最右边的。尽管如此我们也可以认为RANSAC算法在剔除错误匹配点上十分好用。

景深落差大的室外场景拼接
原图：

结果图：

从实验结果可得知，在这张长图拼接中，背景的拼接效果比较好，而近景（水壶）在细节上（电线）拼接效果差，可能原因是：电线上特征点匹配对比较少，或者是仍然存在错误的匹配点对。

扩充
根据图像变换矩阵H，可以对相应图像进行变换以确定图像间的重叠区域，并将待融和图像映射到到一幅新的空白图像中形成拼接图。需要注意的是，由于普通的相机在拍摄照片时会自动选取曝光参数，这会使输入图像间存在亮度差异，导致拼接后的图像缝合线两端出现明显的明暗变化。因此，在融和过程中需要对缝合线进行处理。进行图像拼接缝合线处理的方法有很多种，如颜色插值和多分辨率样条技术等。
我们可以在这个实验基础上加入快速简单的加权平滑算法处理拼接缝问题。该算法的主要思想是：图像重叠区域中像素点的灰度值Pixel 由两幅图像中对应点的灰度值Pixel_L和Pixel_R加权平均得到，即Pixel=k× Pixel_L+(1-k)× Pixel_R，其中k是可调因子。通常情况下0