fuzzy c-means 与 k-means实验对比
一、fuzzy c-means(FCM)
1.1 fuzzy c-means算法简介
FCM的C跟K-Means的K是一样的,指的是聚类的数目。F–Fuzzy是模糊的意思,指的是”一个事件发生的程度“,用在我们的聚类上面,第一条记录以怎样的概率或者说程度属于第一类,又以怎样的程度属于第二类等等。跟传统的聚类有所区别的地方就是,他改变了传统分类的时候非此即彼的一个现象,一个对象可以以不同的程度同时属于多个类。
FCM算法首先是由E. Ruspini提出来的,后来J. C. Dunn与J. C. Bezdek将E. Ruspini算法从硬聚类算法推广成模糊聚类算法。FCM算法是基于对目标函数的优化基础上的一种数据聚类方法。聚类结果是每一个数据点对聚类中心的隶属程度,该隶属程度用一个数值来表示。FCM算法是一种无监督的模糊聚类方法,在算法实现过程中不需要人为的干预,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的。
1.2 fuzzy c-means算法实现原理
模糊c均值聚类融合了模糊理论的精髓。相比较于k-means的硬聚类,模糊c提供了更加灵活的聚类结果。因为大部分情况下,数据集中的对象不能划分成为明显分离的簇,因此,对每个对象和每个簇赋予一个权值,指明对象属于该簇的程度。
隶属度函数是表示一个对象x隶属于集合A的程度的函数,通常记做μA(x), 其自变量范围是所有可能属于集合A的对象(即集合A所在空间中的所有点),μ A(x)的取值范围是[0,1],即0≤= μ A(x)<=1。越接近于1表示隶属度越高,反之越低。
算法的总概况为:给每个样本赋予属于每个簇的隶属度函数。通过隶属度值大小来将样本归类。
流程图:
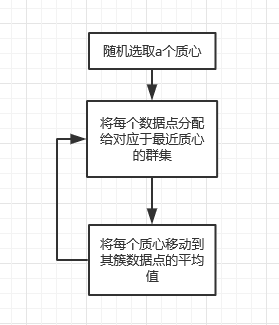
即有a个类,共有N个数据,对于某一数据,其在所有类的隶属度值的和为1,
对于某一个类,所有数据的隶属度值和小于N。
1.3关于k均值与模糊c均值的区别
k均值聚类:是一种硬聚类算法,隶属度只有两个取值:0或1,其提出的基本根据是“内误差平方和最小化” 的准则,进行相关的必要调整优先进行优化看是经典的欧拉距离,同样可以理解成通过对于cluster的类的内部的误差求解误差的平方和来决定是否完成相关的聚类操作。
模糊的c均值聚类算法: 是一种模糊聚类算法,是k均值聚类算法的推广形式,隶属度取值为[0 1] 区间内的任何数,提出的基本根据是“类内加权误差平方和最小化”准则。
这两个方法都是迭代求取最终的聚类划分,即聚类中心与隶属度值。两者都不能保证找到问题的最优解,都有可能收敛到局部极值,模糊c均值甚至可能是鞍点。
二、实验
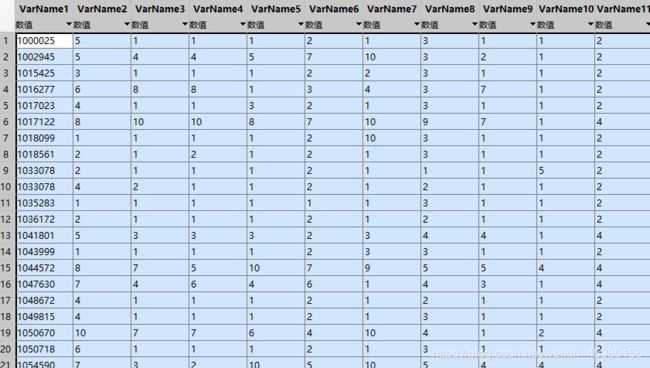
2.1数据收集及细节描述
数据集来源:http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Original)
选用的数据类型为:Breast Cancer Wisconsin (Original) Data Set,中文名称为:威斯康星州乳腺癌数据集。这些数据来源美国威斯康星大学医院的临床病例报告,每条数据具有11个属性。下载下来的数据文件格式为“.data”。
属性特称如下:

1、 样品编号
2、块厚度
3、细胞大小均匀性
4、细胞形态均匀性
5、边缘粘附力
6、单上皮细胞尺寸
7、裸核
8、Bland染色质
9、正常核仁
10、核分裂
11、分类
在设计中从标号2取到标号9的数据作为特征属性,标号11的数据作为分类的类别,值为2的为良性,为4的是恶性。每个特征取值范围都为1~10。数据量为699,作为特征属性的有八种。
2.3 实现代码
main.m
clc;clear;
%load('matlab.mat')%加载测试数据
data=importdata('breast-cancer-wisconsin.data');%加载测试数据
%load('test.txt')%加载测试数据
%[f1,f2,f3,f4,f5] = textread('test.txt' , '%f%f%f%f%f');
N0 =1 ; %从多少列开始的数据进行预测分类
N1 = size(data,1);%所有数据的行数
data=data(N0:N1,:);%只选取需要测试的数据
data1=data(:,[2,3,4,5,6,7,8,9]);
%%
% [2,4,7,9] 2:size(data,2)-1
opts = statset('Display','final');%控制选项
[idx,ctrs,result,D] = kmeans(data1,2,... %data1为要分类的数据,2为分类的类别数,本文只有2类
'Distance','city',... %选择的距离的计算方式
'Options',opts); % 控制选项,参考matlab帮助
%%
m=size(idx,1);
totalSum = 0 ;%总的正确率
t=data(:,1);
for i = 1 : m
if(idx(i,1)==1)
t(i,1)=4;
else
t(i,1)=2;
end
end
d2 = data(:,11);%提取原始数据中属于第1类的数据的最后一列
%t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列
for i = 1 : m
if(t(i,1)==d2(i,1))
totalSum=totalSum+1;
end
end
size(t,1)%总数
totalSum
rate = totalSum/size(t,1)%良性的个数
%%
figure(1);
x1 =1;%第x1个属性
x2 =1 ;%第x2个属性
plot(1:sum(idx==1),data1(idx==1,x1),'r.','MarkerSize',12);
hold on ;
plot(sum(idx==1)+1:sum(idx==1)+sum(idx==2),data1(idx==2,x1),'b.','MarkerSize',12);
xlabel('记录数');
ylabel('属性值');
title('属性9的值分布');
axis([0 700 0 10])
figure(2);
%plot3(data1(:,1),data1(:,2),data1(:,3),'r.','MarkerSize',12)
plot(data1(idx==1,1),data1(idx==1,2),'r.','MarkerSize',12)
hold on
plot(data1(idx==2,1),data1(idx==2,2),'b.','MarkerSize',12)
plot(ctrs(:,1),ctrs(:,2),'kx',...
'MarkerSize',12,'LineWidth',2)
plot(ctrs(:,1),ctrs(:,2),'ko',...
'MarkerSize',12,'LineWidth',2)
%legend('Cluster 1','Cluster 2','Centroids','Location','NW')
grid on;%表示在画图的时候添加网格线
%%
data1=data(:,[2,3,4,5,6,7,8,9]);
figure(3);
[center,U,obj_fcn] = fcm(data1,2);
subplot(1,2,1);
plot(data1(:,1), data1(:,2),'o');
hold on;
maxU = max(U);
% Find the data points with highest grade of membership in cluster 1
index1 = find(U(1,:) == maxU);
% Find the data points with highest grade of membership in cluster 2
index2 = find(U(2,:) == maxU);
plot(data1(index1,1),data1(index1,2),'ob');
plot(data1(index2,1),data1(index2,2),'or');
% Plot the cluster centers
plot(center(1,1),center(1,2),'xb','MarkerSize',15,'LineWidth',3)
plot(center(2,1),center(2,2),'xr','MarkerSize',15,'LineWidth',3)
title('分类结果')
subplot(1,2,2);
plot(obj_fcn)
title('目标函数J的变化')
hold off;
%%
U=U';
m=size(U,1);
n=size(U,2);
for i = 1 : m
for i = 1 : n
[p , index] = max(U,[],2 ) ;
end
end
totalSum2 = 0 ;%总的正确率
t=data(:,1);
for i = 1 : m
if(index(i,1)==1)
t(i,1)=4;
else
t(i,1)=2;
end
end
d2 = data(:,11);%提取原始数据中属于第1类的数据的最后一列
%t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列
for i = 1 : m
if(t(i,1)==d2(i,1))
totalSum2=totalSum2+1;
end
end
size(t,1)%总数
totalSum2
rate2 = totalSum2/size(t,1)%良性的个数
myKMeans.m
参数解释:
N是数据一共分多少类
data是输入的不带分类标号的数据
u是每一类的中心
re是返回的带分类标号的数据
function [u,re]=myKMeans(x,k)
%% 选择k个初始中心点,随机生成
[m,n]=size(x); %m是数据个数,n是数据维数
ma=zeros(n); %每一维最大的数
mi=zeros(n); %每一维最小的数
u=zeros(k,n); %随机初始化,最终迭代到每一类的中心位置
for i=1:n
ma(i)=max(x(:,i)); %每一维最大的数
mi(i)=min(x(:,i)); %每一维最小的数
for j=1:k
u(j,i)=ma(i)+(mi(i)-ma(i))*rand(); %随机初始化,不过还是在每一维[min max]中初始化好些
end
end
%% 分类 更新中心点
while 1
pre_u=u; %上一次求得的中心位置
for i=1:k
tmp{i}=[]; % 公式一中的x(i)-uj,为公式一实现做准备
for j=1:m
tmp{i}=[tmp{i};x(j,:)-u(i,:)];%tmp存放到u{i}的距离 但是是3个维度的
end
end
quan=zeros(m,k);%全为0
for i=1:m %公式一的实现
c=[];
for j=1:k
c=[c norm(tmp{j}(i,:))];%如果A为矩阵 n=norm(A) 返回A的最大奇异值,即max(svd(A))
%第i行的所有列
%取距离那个中心点{j}比较近 c存放到u{i}的距离(比较好比较的版本)一个维度
end
[junk index]=min(c);%找到距离中心点最小的值
quan(i,index)=1;%分类矩阵 0,1
end
for i=1:k %公式二的实现
for j=1:n
u(i,j)=sum(quan(:,i).*x(:,j))/sum(quan(:,i));%属于这个类别的
end
end
if norm(pre_u-u)<0.1 %不断迭代直到位置不再变化
break;
end
end
%% 标记数据
re=[];
for i=1:m
tmp=[];
for j=1:k
tmp=[tmp norm(x(i,:)-u(j,:))];
end
[junk,index]=min(tmp);
re=[re;x(i,:) index];
end
myfcm.m
function [R, V,objFcn] = myfcm(data, k)
%%
T = 100;%默认迭代次数为100
epsm = 1.0e-6; %默认收敛精度
m = 2; %默认模糊系数值为2
%%
[n, s] = size(data);
% 初始化隶属度矩阵U(0),并归一化
U0 = rand(k, n);
temp = sum(U0,1);
for i=1:n
U0(:,i) = U0(:,i)./temp(i);
end
iter = 0;
V(k,s) = 0; R(k,n) = 0; distance(k,n) = 0;
%%
while( iter<T )
iter = iter + 1;
% U = U0;
% 更新V(t)
Um = U0.^m;
V = Um*data./(sum(Um,2)*ones(1,s)); % 公式1
% 更新U(t)
for i = 1:k
for j = 1:n
distance(i,j) = sqrt(sum((data(j,:)-V(i,:)).^2)); % 公式2
end
end
R=1./(distance.^m.*(ones(k,1)*sum(distance.^(-m))));
objFcn(iter) = sum(sum(Um.*distance.^2));
%%
% FCM算法停止条件
if norm(R-U0,Inf)<epsm
break
end
U0=R;
end
test_my.m
测试自己定义的k-means 和c-means
clc;clear;
%测试数据中总共683条,其中良性共444条,恶性共239条:
%load('matlab.mat')%加载测试数据
data=importdata('breast-cancer-wisconsin.data');%加载测试数据
%load('test.txt')%加载测试数据
%[f1,f2,f3,f4,f5] = textread('test.txt' , '%f%f%f%f%f');
N0 =1 ; %从多少列开始的数据进行预测分类
N1 = size(data,1);%所有数据的行数
data=data(N0:N1,:);%只选取需要测试的数据
data1=data(:,[2,3,4,5,6,7,8,9]);
% [2,4,7,9] 2:size(data,2)-1
%%
% opts = statset('Display','final');%控制选项
% [idx,ctrs,result,D] = kmeans(data1,2,... %data1为要分类的数据,2为分类的类别数,本文只有2类
% 'Distance','city',... %选择的距离的计算方式
% 'Options',opts); % 控制选项,参考matlab帮助
[ctrs,idx]=myKMeans(data1,2);
%%
m=size(idx,1);
totalSum = 0 ;%总的正确率
t=data(:,1);
for i = 1 : m
if(idx(i,9)==2)
t(i,1)=4;
else
t(i,1)=2;
end
end
d2 = data(:,11);%提取原始数据中属于第1类的数据的最后一列
%t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列
for i = 1 : m
if(t(i,1)==d2(i,1))
totalSum=totalSum+1;
end
end
size(t,1)%总数
totalSum
rate = totalSum/size(t,1)%良性的个数
figure;
hold on;
for i=1:m
if idx(i,9)==1
plot3(data1(i,1),data1(i,2),data1(i,3),'ro');
elseif idx(i,9)==2
plot3(data1(i,1),data1(i,2),data1(i,3),'bo');
else
plot3(data1(i,1),data1(i,2),data1(i,3),'ro');
end
end
plot3(ctrs(:,1),ctrs(:,2),ctrs(:,3),'kx','MarkerSize',14,'LineWidth',4);
grid on;%表示在画图的时候添加网格线
三、实验分析
3.1结果分析
利用MATLAB的函数实现数据的分类
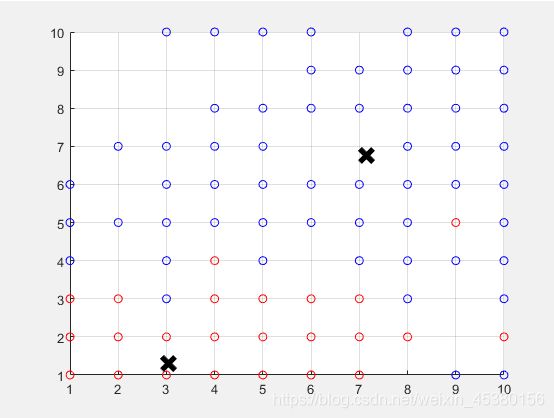
当划分为两类k-means算法的数据分布情况及分类结果



699个数据中良性的个数659个,分类的正确率为94.28%。
c-means分类结果和目标函数的变化:
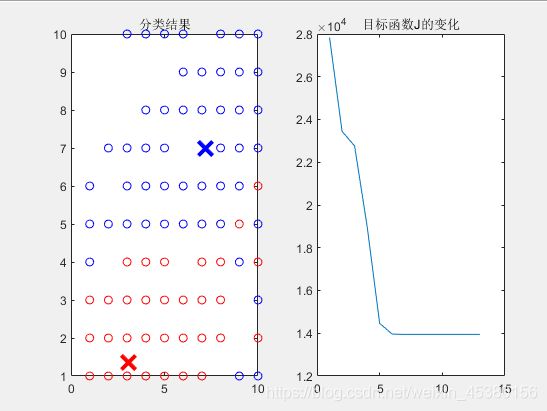
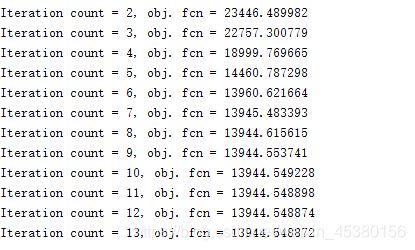

良性的个数677个,分类正确率为95.42%
两种算法的准确率可以发现,用c-means得到的分类正确率更高,分类效果较好。
测试的算法