Android 进阶——高级UI必知必会之Path和贝塞尔曲线（五）

引言

在Android开发中经常会碰到自定义控件，自定义控件涉及的内容比较多，如测量和绘制、事件分发的处理、动画效果的渲染与实现，前面的文章已经介绍了绘制的相关知识，而一些曲线或曲面的UI效果离不开Path和贝塞尔曲线(Bézier curve)，那么到底什么是贝塞尔曲线，它拥有哪些特点，如何结合Path绘制出酷炫的UI效果呢？相关系列文件链接如下：

• Android进阶——高级UI必知必会之2D绘制与Paint的基础应用（一）
• Android进阶——高级UI必知必会之2D绘制与使用Paint对图形进行渲染和滤镜混合处理（二）
• Android进阶——高级UI必知必会之Android坐标系与Canvas小结（三）
• Android 进阶——高级UI必知必会之统一可绘制概念Drawable详解（四）
• Android 进阶——高级UI必知必会之Path和贝塞尔曲线（五）
• Android 进阶——借助PathMeasure打造酷炫Path特效

一、Path概述

Path是由直线段，二次曲线和三次曲线组成的复合几何路径，是一个封装类可以指导Paint的绘制轨迹和方向。可以使用canvas.drawPath（path，paint）进行填充或描边绘制（基于Paint的Style），也可以用于剪切或在路径上绘制文本，简而言之，Path只是负责具体图形的轮廓，需要调用Canvas的drawPath方法之后才真正显示出来

二、贝塞尔曲线的历史故事

贝塞尔曲线(Bézier curve)又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝赛尔曲线由线段与节点组成，其中节点是可拖动的支点，线段像可伸缩的皮筋，（我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的）。贝塞尔曲线是计算机图形学中相当重要的参数曲线，它是依据四个位置任意的点坐标绘制出的一条光滑曲线。贝塞尔曲线的有趣之处更在于它的“皮筋效应”，（即随着点有规律地移动，曲线将产生皮筋伸引一样的变换，带来视觉上的冲击）。1962年法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式（德卡斯特里奥算法），因此按照这样的公式绘制出来的曲线就用他的姓氏来命名是为贝塞尔曲线。简而言之，贝塞尔曲线有以下特性：

• 可精确画出光滑的曲线
• 皮筋效应

才被广泛使用于各种酷炫的UI效果之中，要记住任何曲线都是由一段段线段连接起来的。

三、绘制贝塞尔曲线的原理

贝赛尔曲线的本质是通过数学计算公式去计算得到一系列的点，再把这些点平滑的连接起来，形成一条平滑的曲线，而Bezier曲线是由一系列点来控制曲线状态的，这些点可分为两类：

• 数据点——用于确定曲线的起始和结束位置
• 控制点——用于确定曲线的弯曲程度（由公式推导出来）

根据数学公式求出这些控制点再将它们平滑的连接起来就得到贝塞尔曲线。

1、一阶（线性）贝塞尔曲线

一阶贝塞尔曲线只需要由两个数据点来确定曲线的起始和结束位置（两个数据点连接构成一条线段，因此叫一阶）就可以绘制出来，比如给定数据点P0、P1，一阶贝塞尔曲线只是一条两点之间的直线，这条线由下式给出：


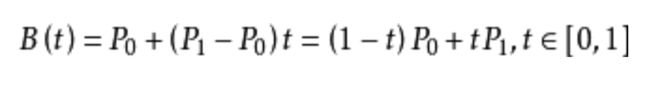
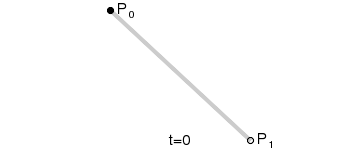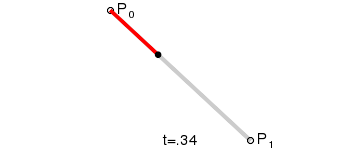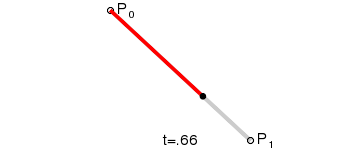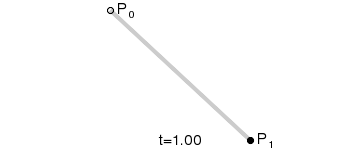
通过上面的公式根据t的就可以得出对应线段上那个控制点的坐标，就能够实现两个数据点控制的一条直线的目标。

2、二阶贝塞尔曲线

二阶贝塞尔曲线则需要由三个数据点来确定（因为三个不在一直线上的数据点首尾连接可以构成两条线段，因此叫二阶），二阶贝塞尔曲线的路径是由两个数据点 和一个控制点去决定的。二阶贝塞尔曲线是由一个控制点去控制一条的曲线,而曲线的运动是由两个线段所控制的，具体绘制二阶贝塞尔曲线如下：

再看不懂可以看下网上借来的动图：

动图里的P0、P1、P2分别代表的是上图的：P0 == A；P1 == B；P2 == C。那么这个黑色点，代表的就是F点，绿色线段的2个端点（P0-P1线段上的绿色点，代表是就是D点，P0-P2线段上的绿色点，代表是就是E点）。

线段上面点的获取，必须要满足等比关系,计算公式如下：

简而言之，要想控制曲线的弯度，只需要知道两个数据点（起始点和结束点）和一个控制点。

3、三阶贝塞尔曲线与N阶贝塞尔曲线

其实三阶贝塞尔与四阶贝赛尔曲线以及N阶贝赛尔曲线曲线的规则都是一样的，都是先在线段上找点，这个点必须要满足等比关系，然后依次连接，所谓三阶贝塞尔曲线，是有三个线段控制的，绘制步骤也大同小异:

同样看下网上借来的动图

线段上面点的获取，必须要满足等比关系,计算公式如下：

那么四阶贝赛尔曲线的实现步骤也类似，逐层降阶，平面上先选取5个点（5点4线）、依次选点（满足等比关系）、依次连接、根据计算规则找到所有的点

五阶贝塞尔曲线：

那么由点P0、P1、…、Pn所决定的N阶贝兹曲线通用公式为：

四、Path的基础应用

Path主要就是绘制轮廓的，而轮廓在真正被绘制到Canvas之前，可以进行一系列的运算操作，从而得出各种各样的轮廓。

1、添加轮廓系方法

Path中类似addArc之类的方法是用于添加指定形状的轮廓，以下只列出部分方法（重载的不包含）

方法名	说明
void addArc(RectF oval, float startAngle, float sweepAngle)	在当前路径实例上添加上弧形的轮廓
void addCircle(float x, float y, float radius, Path.Direction dir)	添加一个闭环的圆形，其中Path.Direction表示绘制方向（在进行PathMesure时影响对应的值），逆时针Path.Direction.CCW、 顺时针Path.Direction.CW
void addOval(RectF oval, Path.Direction dir)	添加椭圆轮廓
void addPath(Path src, Matrix matrix)	添加指定的Path和利用矩阵进行变化
void addRect(RectF rect, Path.Direction dir)	添加矩形轮廓
void addRoundRect(RectF rect, float rx, float ry, Path.Direction dir)	添加圆矩形轮廓

Path path=new Path();
//添加矩形， 圆角矩形， 椭圆， 圆， 路径， 圆弧轮廓
path.addCircle(300, 400, 240, Path.Direction.CW);
path.addArc(200, 200, 300, 300, 0, -90);
path.arcTo(200, 200, 300, 300, 0, 90, true);
path.addOval(300, 300, 400, 450, Path.Direction.CW);
path.addRect(100, 400, 300, 500, Path.Direction.CW);
path.addRoundRect(100, 600, 300, 700, 20, 40, Path.Direction.CW);
canvas.drawPath(path, mPaint);

2、轮廓之间进行运算的方法

对轮廓进行逻辑运算，其实和数学中集合的运算类似，Path提供了op方法对两个Path进行布尔运算(即取交集、并集等操作)，进行op方法操作之后，只有调用op方法的路径才会改变，而传入的路径不受影响。

运算符	说明
Path.Op.DIFFERENCE	减去path1中path1与path2都存在的部分，path1 = (path1 - (path1 ∩ path2))
Path.Op.INTERSECT	保留path1与path2共同的部分，path1 = path1 ∩ path2
Path.Op.UNION	取path1与path2的并集，path1 = path1 ∪ path2
Path.Op.REVERSE_DIFFERENCE	与DIFFERENCE刚好相反，path1 = path2 - (path1 ∩ path2)
Path.Op.XOR	与INTERSECT刚好相反，path1 = (path1 ∪ path2) - (path1 ∩ path2)

public class PathView extends View {
    private Path mPath1 = new Path();
    private Path mPath2 = new Path();
    private Paint mPaint = new Paint();
    public PathView(Context context) {
        super(context);
        mPaint.setColor(Color.GREEN);
        mPaint.setStrokeWidth(20);
        mPaint.setStyle(Paint.Style.STROKE);
    }

    @RequiresApi(api = Build.VERSION_CODES.LOLLIPOP)
    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        mPath1.addCircle(200, 200, 100, Path.Direction.CW); //绘制圆
        mPath2.addCircle(300, 300, 100, Path.Direction.CW);
         //mPath1.op(mPath2,Path.Op.DIFFERENCE);
        // mPath1.op(mPath2,Path.Op.INTERSECT);
        // mPath1.op(mPath2,Path.Op.UNION);
        // mPath1.op(mPath2,Path.Op.XOR);
        mPath1.op(mPath2, Path.Op.REVERSE_DIFFERENCE);
        canvas.drawPath(mPath1, mPaint);
        mPaint.setColor(Color.RED);
        mPaint.setStrokeWidth(4);
        canvas.drawPath(mPath2, mPaint);
    }
}

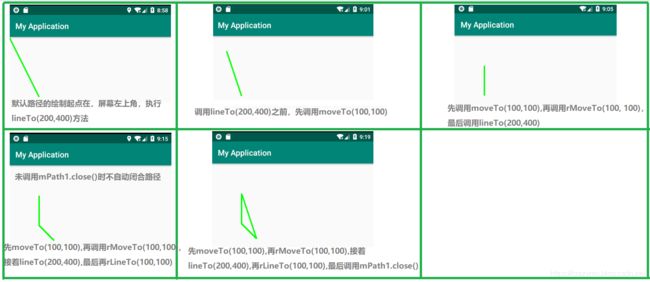
3、路径上的移动连线和闭合

运算符	说明
void moveTo(float x, float y)	将路径的绘制位置的起点定在（x,y）的位置（默认的起点位于屏幕的左上角）
void rMoveTo(float dx, float dy)	在前一个点的基础上开始绘制，如果前面一个点是（x,y）rMoveTo(dx,dy)相当于moveTo(x+dx,y+dy),如果前面没有调用moveTo，相当于从(dx,dy)开始绘制
void lineTo(float x, float y)	相当于是设置了终点位置，把起点和终点用直线连接起来
void rLineTo(float x, float y)	与rMoveTo类似，升级版的lineTo
void close()	使得路径闭环

4、绘制2阶、3阶贝塞尔曲线

Path的系统API只提供了绘制2阶和3阶贝塞尔曲线的功能，要想绘制多阶只能自己去实现。

• quadTo(float x1, float y1, float x2, float y2) 绘制二阶贝塞尔曲线，如果没有执行moveTo方法设置起点，则(x1,y1)变为控制点，起始点为（0,0）；而执行了moveTo之后起始点为moveTo的坐标，控制点为（x1,y1）,终点都为(x2，y2)。
  

其中的橙色线段和坐标都是我自己手工绘制的，代码只是绘制了绿色部分的。

• void rQuadTo(float dx1, float dy1, float dx2, float dy2)

升级版的quadTo与上面的rMoveTo类似。

mPath1.moveTo(100, 100);
mPath1.quadTo(400, 200, 50, 500);//二阶贝塞尔曲线
canvas.drawCircle(100, 100, 10, mPaint);
canvas.drawCircle(400, 200, 10, mPaint);
canvas.drawCircle(50, 500, 10, mPaint);
canvas.drawPath(mPath1, mPaint);
canvas.save();
mPaint.setStrokeWidth(4);
mPaint.setColor(Color.RED);
canvas.restore();
mPaint.setColor(Color.RED);
//rQuadTo方法是基于当前点坐标系(偏移量)
mPath1.rQuadTo(300, 100, -90, 400);
canvas.drawPath(mPath1, mPaint);

• cubicTo(float x1, float y1, float x2, float y2, float x3, float y3) 阶绘制3阶贝塞尔

mPath1.moveTo(100, 100);
mPath1.cubicTo(400, 200,10, 500,300, 700);
canvas.drawCircle(100, 100, 10, mPaint);
canvas.drawCircle(400, 200, 10, mPaint);
canvas.drawCircle(10, 500, 10, mPaint);
canvas.drawCircle(300, 700, 10, mPaint);
canvas.drawPath(mPath1, mPaint);