数值分析和SVM讲解（上）

此次是对原来的文章进行的第一次修改。起因是通过参加公司实习，更加确定了基础知识的重要性。由此，重新阅读相关的知识和文献，希望能够提炼出更加符合逻辑的知识。本系列文章主要针对的是支持向量机的讲解。对此，我个人起的标题是《数值分析和SVM讲解》，一方面是为了区分其他系列的数学知识（比较前面的线性代数和概率论，我们这里更加侧重高数的知识），另一方面也是强调数值分析在机器学习当中的重要程度。

其次，本系列文章将会和前面两篇《PCA线性代数讲解》《概率论及logistic回归讲解》相呼应，同时也相当于是关于《深度学习》这本书中前五章的总结（数学基础和机器学习部分）。谈到后面机器学习实例时，我将更多的谈到数据维度和风险函数（代价函数）之类的思想，最后将PCA、logistic回归和SVM它们做个联系。

1.1数值分析

先来维基百科上的定义：

数值分析(Wiki)：是指在数学分析（区别于离散数学）问题中，对使用数值近似（相对于一般化的符号运算）算法的研究。数值分析的目的是设计及分析一些计算的方式，可针对一些问题得到近似但够精确的结果。数值分析方法分为两种：直接法和迭代法。直接法利用固定次数的步骤求出问题的解，包括求解线性方程组的高斯消去法和解析法，求解线性规划的单纯形法等；迭代法是通过从一个初始估计出发寻找一系列近似解来解决问题的数学过程。和直接法不同，用迭代法求解问题时，其步骤没有固定的次数，而且只能求得问题的近似解，所找到的一系列近似解会收敛到问题的精确解，然后利用审敛法来判别所得到的近似解是否会收敛，包括牛顿法、二分法、梯度下降方法等。一般我们采用迭代法对问题进行求解。

大多数机器学习算法（这里更特指监督学习）都涉及某种形式的优化。优化指的是改变 x 以最小化或最大化某个函数 f(x) 的任务。我们通常以最小化 f(x) 指代大多数最优化问题。最大化可经由最小化算法最小化 −f(x) 来实现。我们把要最小化或最大化的函数称为目标函数（objective function）或准则（criterion）。当我们对其进行最小化时，我们也把它称为代价函数（cost function）、损失函数（loss function）或误差函数（error function）。在前面一篇《概率论及logistic回归讲解》中，我们采用了第二种机器学习的视角看待logistic回归时候，我们展示了常用的损失函数。

在这里我们继续深入，李航博士《统计学习方法》书中（好书，推荐。理由是每章会有例子进行展示），有过对“损失函数”的升级版“风险函数”的讨论，其中他认为“损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏”。所以说，我们认为后者更有研究的意义，其实在我看来，这个“风险函数”就是对全体样本作代价函数（代价求和或者求平均）。特殊的，训练数据集的平均代价我们称为“经验风险”。

引入了“风险函数”，那么对于样本我们还需要考虑“过拟合”的问题。啥意思，当数据样本本身具有“不可信”的部分时，一旦样本量比较小，那么我们得出的模型可能是比较糟糕的（分类或者回归效果很差）。由此引出关于“风险函数”的两个策略：“经验风险最小化”和“结构风险最小化”。

通俗理解，“经验风险最小化”只是单纯的最小化“经验风险”，即最小化平均代价函数；“结构风险最小化”即正则化，在“经验风险函数”基础上考虑正则化项或者惩罚项，使原来的目标函数变得更为复杂，当然这样也就更加合理（现在基本都是这个策略）。

1.2最优化

上述中，我们已经建立了咱们的优化模型，接下来咱们需要求解这个目标函数得出最优解。所以我们的目标也就从建立目标函数过渡到如何求解最优解，而后者也就是这一节的主要内容。

通常我们需要求解的最优化问题有如下几类：
(i)无约束优化问题，具体而言1：

(ii) 有等式约束的优化问题，具体而言：

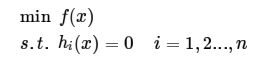
(iii) 有不等式约束的优化问题，具体而言：

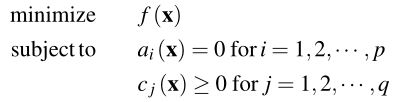
对于第(i)类的求解，知识点在于导数（标量）、梯度（向量）和Hessian矩阵。举例而言，如果自变量为标量，求解min f(x)。其方法即为：对x关于f(x)求导令其为零得到候选点，再根据二阶导数判断是否为极值点。（高数中二阶导数与0的比较，其实是判断f(x)凹凸性的标志）。如果自变量为矢量，则牵扯到梯度（多维偏导数形态）和Hessian矩阵的知识。
工程上，我们往往采用迭代法来求解无限制优化问题4：

其中最重要的步骤为2，根据dk的不同计算方法，我们有梯度下降法、牛顿法（这两种方法证明与泰勒公式有关）等等优化方法。更多的，可以看此链接：http://www.cnblogs.com/zhangchaoyang/articles/2600491.html

对于第(ii)类的求解，知识点在于拉格朗日乘子(Lagrange Multiplier)。流程上把等式约束hi(x)用一个系数与f(x)写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。

下面我们看Wikipedia上解释拉格朗日乘子法的合理性的，假设有等式约束优化问题如下5：

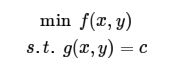
如下图所示6：

绿线标出的是约束g(x,y) = c的点的轨迹。蓝线是f(x,y)的等高线。箭头表示梯度，和等高线的法线平行。从图上可以直观地看到在最优解处，f和g的法线方向刚好相反（或者说叫梯度共线），即下列步骤7即为5的求解过程：

另外，上式7也为求解下面无约束优化问题8的候选解：

捋一捋逻辑，等式约束优化问题5的解由7得出，而求解无约束优化问题8的候选解与7等价，所以等式约束优化问题5和无约束优化问题8的求解步骤一致，换句话说，解问题5可以等价于求解问题8。

对于第(iii)类的优化问题，知识点为KKT条件。同样地，我们把所有的等式、不等式约束与f(x)写为一个式子，也叫拉格朗日函数，系数也称拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件称为KKT条件。我们通过KKT条件求得极值点（候选点）。

KKT条件作为一般限制优化问题极值点的一阶必要条件，内容如下9：

工程上，遇到约束性优化问题，也多用KKT去尝试。但是毕竟不是充要条件（凸优化里才能升级为充要），所以怎么把问题变为凸优化问题，这样可以一取得全局最优，二KKT成为充要条件。

对于KKT如果究其根本，当然是Boyd的《Convex Optimization》，不过比较费时费力，数学功底扎实的可以一探究竟。对于不做要求的同学，可以看看第三个链接和这篇http://www.cnblogs.com/zhangchaoyang/articles/2726873.html。

tips：1第一篇博客讲的是拉格朗日对偶性，主要把KKT怎么来的，以及相关推导叙述一遍，可以作为主要；2.第二篇博客细化了对偶问题和原始问题的变换推导，主要以公式为主，可以作为辅助（文章略有瑕疵，可以看看评论自己琢磨一番）。

最后将第一部分稍作总结：这里引用《统计学习方法》书中1.3节的内容——方法=模型+策略+算法。对于一般的机器学习，尤其是监督学习，我们首先考虑模型的选取，条件概率分布或者决策函数，这就与概率论的知识结合在一起了；选取了模型之后，我们需要考虑按照什么样的准侧进行最优化，即为如何构建最优模型，引出代价函数和风险函数后，我们还有两个策略“经验风险最小化”“结构风险最小化”；最后，考虑如何求解，即为如何构建算法，这部分基本为纯数学优化知识。

---

P_1：文章进行第一次修改，修改标题名由“数值计算”为“数值分析”，重新撰写引言部分并增加数值分析的定义。